 |
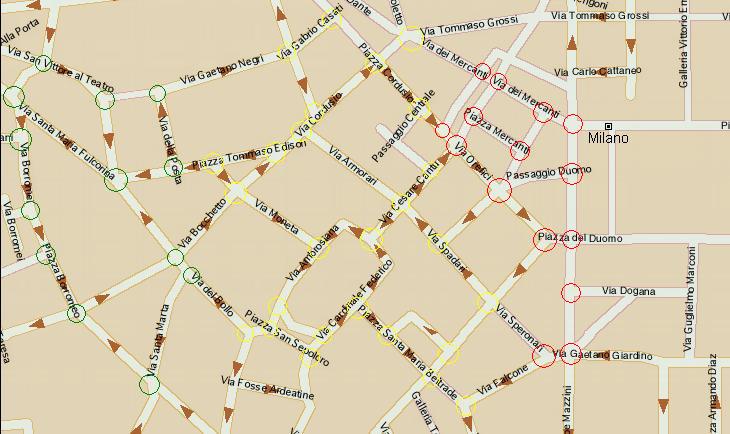
Il giro d'Italia a Milano Gli organizzatori del Giro d’Italia stanno transennando alcune vie del centro di Milano per delimitare le zone interessate al percorso ciclistico. Nella cartina riportata a fianco alcuni incroci sono cerchiati in rosso, alcuni in verde e altri in giallo. Gli incroci in rosso sono quelli sicuramente non transitabili dai non addetti ai lavori, quelli verdi sono liberi. |
| soluzione | |
|
|
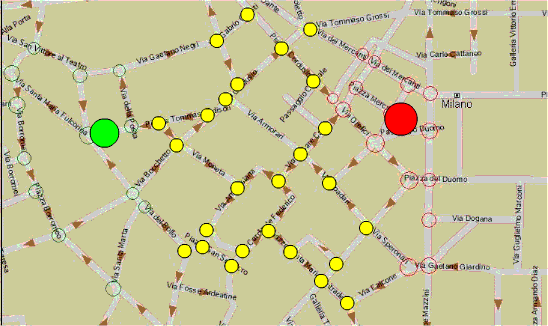
soluzione Le strade da transennare sono 4, tramutando 11 incroci gialli in verde.
La soluzione di Jeff (Gianluca Busan):
Un primo tentativo, per capire l'ordine del problema, è quello di provare a transennare tutti i gialli in verde o in rosso.
Trasformarli tutti in verde significa transennare 7 strade (e sicuramente tra tutte le transennature di cardinalità 7, questa è la migliore)
Trasformarli tutti in rosso significa transennare 4 strade (e sicuramente tra tutte le transennature di cardinalità 4, questa è la peggiore)
Visto che si è interessati a minimizzare in numero di strade transennate, sicuramente trasformare tutto in rosso è preferibile che trasformare tutto in verde.
Perciò la soluzione del problema sarà un numero minore o uguale a 4. E se fosse 4 bisognerebbe cercare quella transennatura che massimizza gli incroci verdi.
Per risolvere il problema facciamo alcune considerazioni:
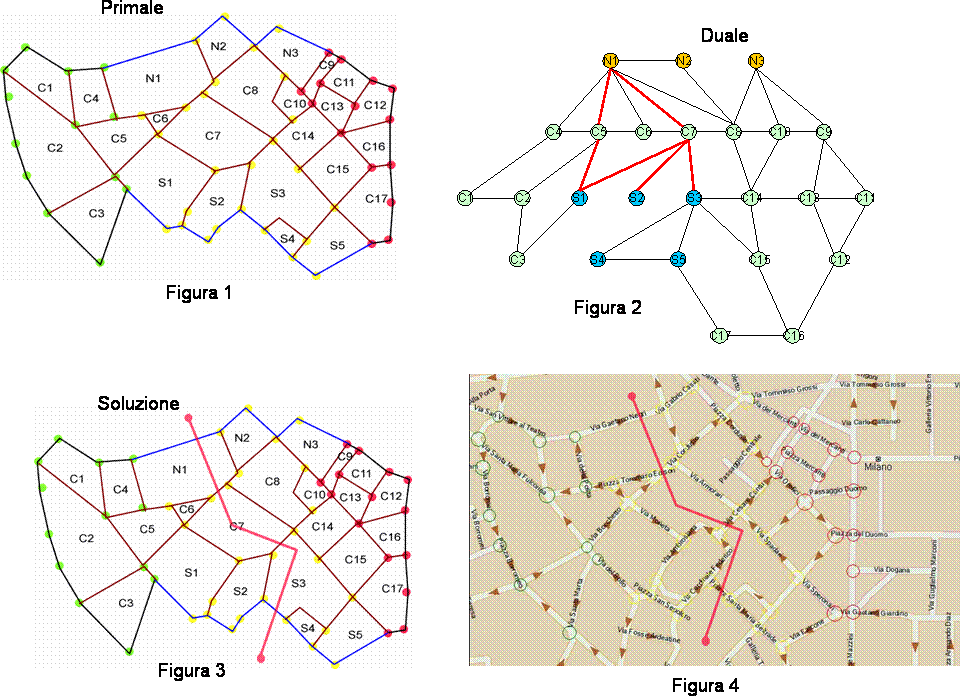
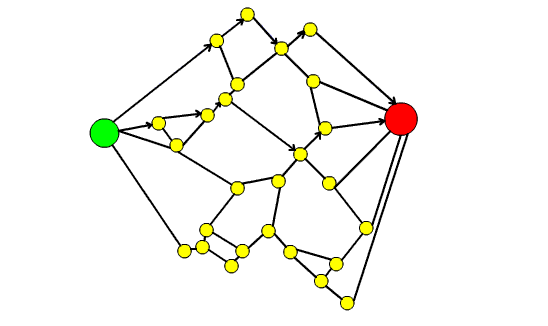
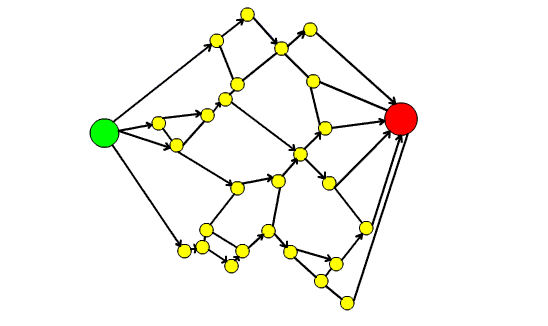
1. costruiamo il grafo associato alla cartina: i nodi sono gli incroci e gli archi sono le strade. E' evidente che il grafo è PLANARE (vedi figura 1 in allegato).
2. dalla teoria dei grafi si sa che si può trasformare tale grafo planare nel grafo duale (vedi figura 2 in allegato): tale grafo ha come nodi le regioni di piano comprese tra gli archi del primale (in figura1 tali aree sono etichettate, in figura 2 i nodi hanno le etichette corrispondenti); due nodi del grafo duale sono collegati da un arco se le corrispondenti aree del primale sono confinanti con almeno un lato (arco)
Nel primale, il problema consiste nel transennare delle strade (togliere degli archi) in modo da creare due sottografi separati tali per cui gli incroci verdi stiano su un sottografo e quelli rossi sull'altro. E' evidente dalla figura 1 che si dovrà sicuramente tagliare un arco a nord ed uno a sud (sono i cammini marcati in blu) altrimenti è possibile andare da un incrocio verde ad uno rosso.
Per esempio (vedi figura): transenniamo un arco a nord ed entriamo nell'area N1, adesso entriamo nell'area C8 transennando l'arco di confine tra N1 e C8, allo stesso modo da C8 potremmo passare in C14 e poi in C15, in S3 e transennare un arco blu a sud: a questo punto se nel passare da un'area all'altra transenniamo la strada di confine (tra le aree) il "cammino" N1-C8-C14-C15-S3 "separa" il grafo primale in due sottografi che soddisfano la condizione di separare gli incroci verdi da quelli rossi. Gli incroci gialli della componente connessa di sinistra diventano verdi quelli di destra rossi. In questo esempio la transennatura ha cardinalità 6 (1 + NUMERO DI NODI NEL CAMMINO N1-C8-C14-C15-S3 ).
E' evidente che "N1-C8-C14-C15-S3" è un cammino ammissibile nel grafo duale (figura 2). Rendere minima la cardinalità della transennatura significa cercare un cammino minimo sul grafo duale.
Per risolvere il problema si deve sicuramente "entrare" in una regione a nord (N1 o N2 o N3) ed "uscire" da una regione a sud (S1, S2, S3, S4, S5) [tali regioni sono quelle che hanno almeno un lato colorato di blu]
Risolvere il problema significa quindi cercare un cammino minimo tra un nodo di tipo Nx ed uno di tipo Sy. Un tale cammino determina una (o più, per esempio se il nodo finale fosse S2, ci sarebbero 3 possibili strade da transennare) sezione del grafo primale in modo da soddisfare la condizione di dividere gli incroci verdi da quelli rossi. A parità di cammino minimo si deve preferire quello che nell'equivalente primale massimizza gli incroci verdi.
In letteratura esistono parecchi algoritmi di cammino minimo: per esempio con l'algoritmo di Bellman-Ford si possono trovare tutti i cammini minimi, per usarlo basta aggiungere un nodo sorgente S e collegarlo ai nodi Nx ed aggiungere un nodo target T e collegarlo con i nodi di tipo Sy; inoltre basta dare peso 1 a tutti gli archi. A questo punto tutti i cammini minimi tra S e T sono anche cammini minimi per il duale e quindi soluzioni probabili per il primale.
Una volta trovati tutti i cammini minimi, si torna al primale e si applicano i tagli, si contano gli incroci gialli da trasformare in verde e si sceglie il "cammino" che massimizza tale numero.
Nel nostro esempio (vedi figura 2) il cammino minimo è lungo 2 (è un grafo talmente semplice che si vede ad occhio: non ci sono archi diretti (cammino lungo 1) tra un Nx e un Sy, però ne esiste almeno uno di lunghezza 2 (N1-C5-S1), perciò il minimo è 2).
Tutti i cammini di lunghezza 2 sono i seguenti:
N1-C5-S1
N1-C7-S1
N1-C7-S2
N1-C7-S3
Tra questi quello che massimizza gli incroci verdi è N1-C7-S3 a cui corrisponde un unico "taglio" del primale (vedi figura 3). Si vede da tale figura che le transenne da mettere sono 4 e che gli incroci gialli trasformati in verde sono 11.
La figura 4 mostra il taglio direttamente sulla cartina originale.
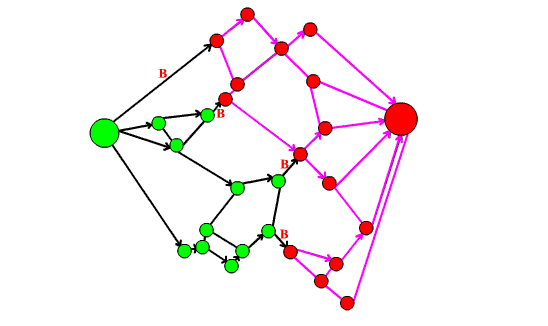
La soluzione di Luca Barletta:
Il quesito si può interpretare nel seguente modo: stiamo cercando un taglio di cardinalità minima su un grafo ciclico non orientato. Un taglio è una partizione del grafo (=la nostra rete stradale) in due componenti connesse, vale a dire due sottografi di n e m nodi (=incroci della rete), con n+m numero totale di nodi del grafo originario; connesse nel senso che in ogni sottografo un nodo è collegato almeno ad un altro del sottografo stesso. L'insieme del taglio ha come elementi gli archi (=strade) che, se tolti, determinano la partizione del grafo.
Cercare un taglio di cardinalità minima del grafo equivale a trovare il flusso massimo sullo stesso grafo: infatti il taglio minimo può essere visto come un "collo di bottiglia" che limita il flusso di una quantità, questo flusso è massimo per il grafo.
Premesso ciò, il quesito poteva essere risolto in 12 passaggi, alcuni dei quali ripetitivi.
- sostituiamo tutti gli incroci verdi con un unico nodo verde e analogamente per gli incroci rossi
- aggiungiamo tutti gli archi del grafo assicurandoci di collegare correttamente i nodi gialli ai nodi rosso e verde
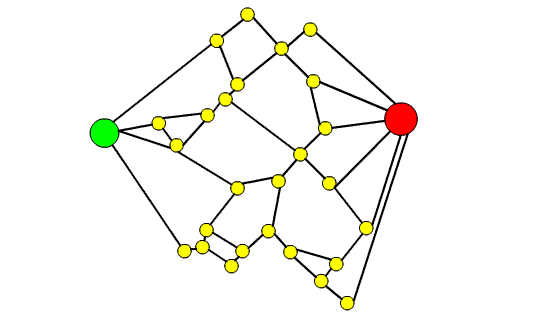
- dobbiamo trovare il flusso massimo: cominciamo a spedire la prima unità di flusso sul grafo su un cammino che vada dal nodo verde al nodo rosso (il cammino deve avere il minor numero di archi possibile)
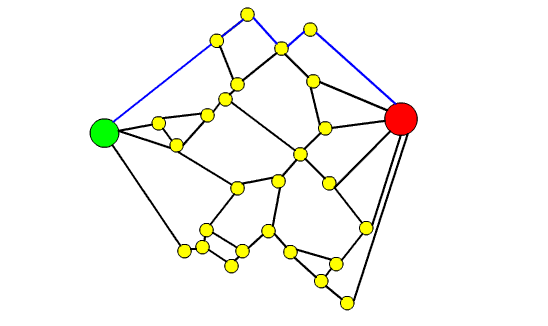
- poichè ogni arco ha capacità unitaria (può essere trasportata solo un'unità di flusso sugli archi), gli archi del cammino minimo trovato precedentemente non sono più utilizzabili; pertanto porremo una freccia su ogni arco del cammino; la freccia è concorde con la direzione verde-rosso del cammino
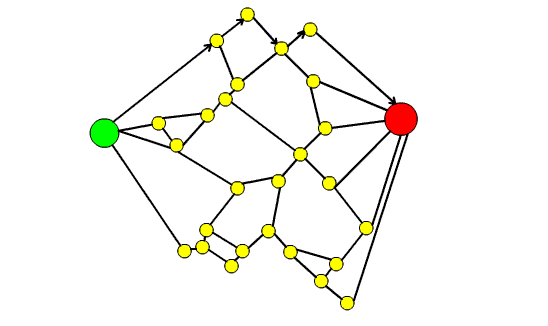
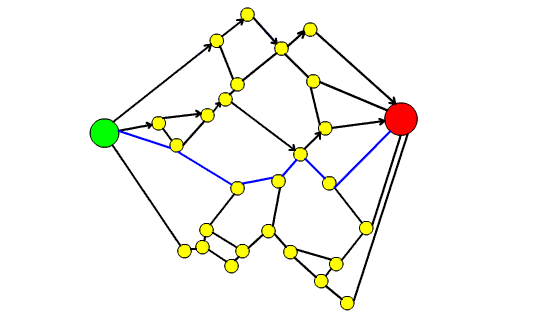
- troviamo il secondo cammino minimo
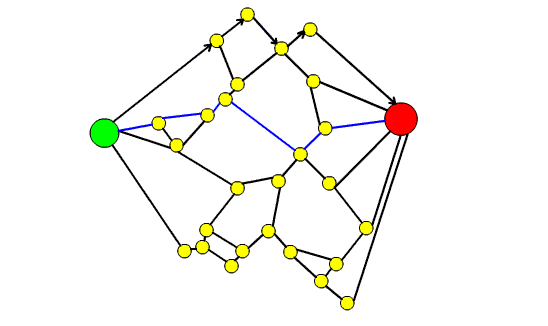
- per le stesse ragioni espresse nel punto 4 procediamo col porre le frecce
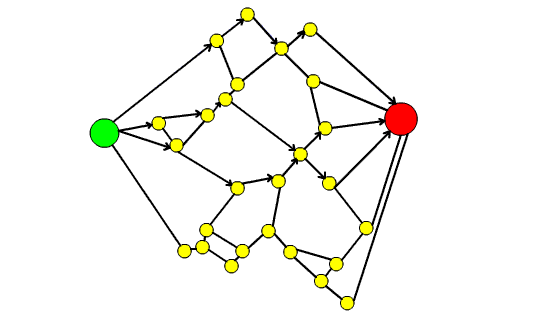
- troviamo il terzo cammino minimo
- per le stesse ragioni espresse nel punto 4 procediamo col porre le frecce
- troviamo il quarto cammino minimo
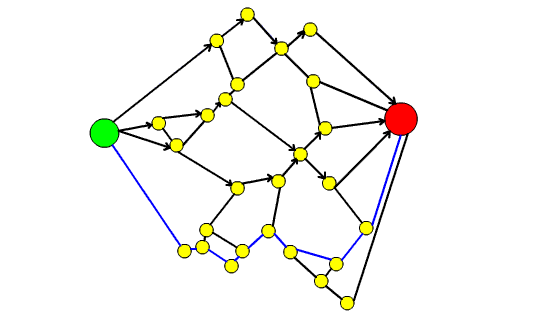
- per le stesse ragioni espresse nel punto 4 procediamo col porre le frecce
- ci accorgiamo che non possiamo più trovare cammini minimi. Esiste un teorema che dice che in un grafo o esiste un cammino che collega il nodo s al nodo t oppure esiste un taglio che partiziona i nodi in due insiemi A e B e tale che s appartiene ad A e t appartiene a B.
Noi siamo giunti alla seconda condizione, abbiamo trovato un taglio perchè non ci sono più cammini minimi; l'insieme degli archi che formano il taglio saranno le strade che verranno transennate.
Per individuare gli archi del taglio facciamo partire un'unità di flusso dal nodo rosso e percorriamo tutti gli archi percorribili, tenendo conto che gli archi senza freccia sono bidirezionali, mentre rispettiamo la direzione degli archi orientati (gli archi percorribili sono evidenziati in rosa e gli archi appartenenti al taglio indicati con la lettera B)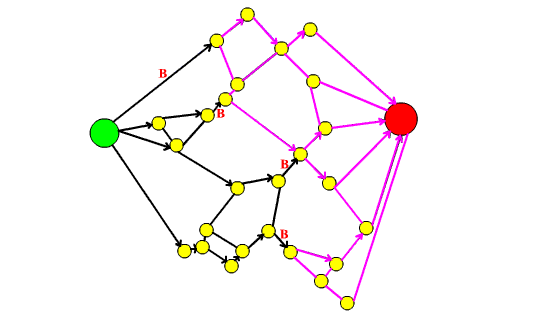
- a questo punto possiamo assegnare il colore definitivo agli incroci gialli (verde o rosso)