Dadi e probabilità
Lanciando tre normali dadi con le facce numerate da 1 a 6, sommando i numeri delle tre facce si può ottenere un numero compreso tra 3 e 18. Non tutti questi numeri hanno però la stessa probabilità di verificarsi. 3 ha probabilità 1/216, 4 ha invece probabilità 3/216 e così via.
Costruire il maggior numero di terne di dadi, con le facce numerate a piacere, in modo che le somme dei numeri sulle tre facce diano numeri consecutivi da 3 in poi e che tutti i numeri abbiamo la stessa probabilità di verificarsi?
Lanciando 3 dadi le possibilità sono 6x6x6=216.
La prima soluzione banale del problema è
(1,1,1,1,1,1)+(1,1,1,1,1,1)+(1,1,1,1,1,1) il numero 3 ha probabilità 216/216 di verificarsi
La seconda soluzione facile del problema è
(1,2,3,4,5,6)+(1,7,13,19,25,31)+(1,37,73,109,145,181) i numeri possibili vanno da 3 a 218, ciascuno con probabilità 1. Come ha osservato BOODOO questa soluzione è strettamente collegata al sistema di numerazione in base 6.
Trovare le altre terne di dadi non è facile.
MATRIX che con questo quesito ha vinto la gara ha utilizzato un programma trovando le seguenti 45 soluzioni
| 1. F= 216 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
2. F=108 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 |
3. F=72 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 3 |
4. F=54 1 1 1 1 1 1 1 1 1 2 2 2 1 1 1 3 3 3 |
5. F=36 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 4 5 6 |
| 6. F=36 1 1 1 1 1 1 1 1 1 2 2 2 1 1 3 3 5 5 |
7. F=36 1 1 1 1 1 1 1 1 1 4 4 4 1 1 2 2 3 3 |
8. F=27 1 1 1 2 2 2 1 1 1 3 3 3 1 1 1 5 5 5 |
9. F=24 1 1 1 1 1 1 1 1 2 2 3 3 1 1 4 4 7 7 |
10. F=18 1 1 1 1 1 1 1 1 1 2 2 2 1 3 5 7 9 11 |
| 11. F=18 1 1 1 1 1 1 1 1 1 3 3 3 1 2 5 6 9 10 |
12. F=18 1 1 1 1 1 1 1 1 1 4 4 4 1 2 3 7 8 9 |
13. F=18 1 1 1 1 1 1 1 1 1 7 7 7 1 2 3 4 5 6 |
14. F=18 1 1 1 2 2 2 1 1 1 3 3 3 1 1 5 5 9 9 |
15. F=18 1 1 1 2 2 2 1 1 1 7 7 7 1 1 3 3 5 5 |
| 16. F=18 1 1 1 4 4 4 1 1 2 2 3 3 1 1 1 7 7 7 |
17. F=12 1 1 1 1 1 1 1 1 2 2 3 3 1 4 7 10 13 16 |
18. F=12 1 1 1 1 1 1 1 1 3 3 5 5 1 2 7 8 13 14 |
19. F=12 1 1 1 1 1 1 1 1 4 4 7 7 1 2 3 10 11 12 |
20. F=12 1 1 1 1 1 1 1 1 7 7 13 13 1 2 3 4 5 6 |
| 21. F=12 1 1 1 2 2 2 1 1 3 3 5 5 1 1 7 7 13 13 |
22. F=12 1 1 1 4 4 4 1 1 2 2 3 3 1 1 7 7 13 13 |
23. F=12 1 1 1 10 10 10 1 1 2 2 3 3 1 1 4 4 7 7 |
24. F=9 1 1 1 2 2 2 1 1 1 3 3 3 1 5 9 13 17 21 |
25. F=9 1 1 1 2 2 2 1 1 1 5 5 5 1 3 9 11 17 19 |
| 26. F=9 1 1 1 2 2 2 1 1 1 13 13 13 1 3 5 7 9 11 |
27. F=9 1 1 1 3 3 3 1 1 1 5 5 5 1 2 9 10 17 18 |
28. F=9 1 1 1 3 3 3 1 1 1 13 13 13 1 2 5 6 9 10 |
29. F=9 1 1 1 4 4 4 1 1 1 7 7 7 1 2 3 13 14 15 |
30. F=9 1 1 1 4 4 4 1 1 1 13 13 13 1 2 3 7 8 9 |
| 31. F=9 1 1 1 7 7 7 1 1 1 13 13 13 1 2 3 4 5 6 |
32. F=8 1 1 2 2 3 3 1 1 4 4 7 7 1 1 10 10 19 19 |
33. F=6 1 1 1 2 2 2 1 1 5 5 9 9 1 3 13 15 25 27 |
34. F=6 1 1 1 2 2 2 1 1 13 13 25 25 1 3 5 7 9 11 |
35. F=6 1 1 1 3 3 3 1 1 5 5 9 9 1 2 13 14 25 26 |
| 36. F=6 1 1 1 3 3 3 1 1 13 13 25 25 1 2 5 6 9 10 |
37. F=6 1 1 1 4 4 4 1 1 7 7 13 13 1 2 3 19 20 21 |
38. F=6 1 1 1 4 4 4 1 1 13 13 25 25 1 2 3 7 8 9 |
39. F=6 1 1 1 7 7 7 1 1 3 3 5 5 1 2 13 14 25 26 |
40. F=6 1 1 1 7 7 7 1 1 13 13 25 25 1 2 3 4 5 6 |
| 41. F=6 1 1 1 10 10 10 1 1 4 4 7 7 1 2 3 19 20 21 |
42. F=6 1 1 1 19 19 19 1 1 2 2 3 3 1 4 7 10 13 16 |
43. F=6 1 1 1 19 19 19 1 1 3 3 5 5 1 2 7 8 13 14 |
44. F=6 1 1 1 19 19 19 1 1 4 4 7 7 1 2 3 10 11 12 |
45. F=6 1 1 1 19 19 19 1 1 7 7 13 13 1 2 3 4 5 6 |
Con il computer è facile, penserete. Non è proprio così. Le possibilità sono tante che se non si trova un buon algoritmo si può aspettare la soluzione per anni.
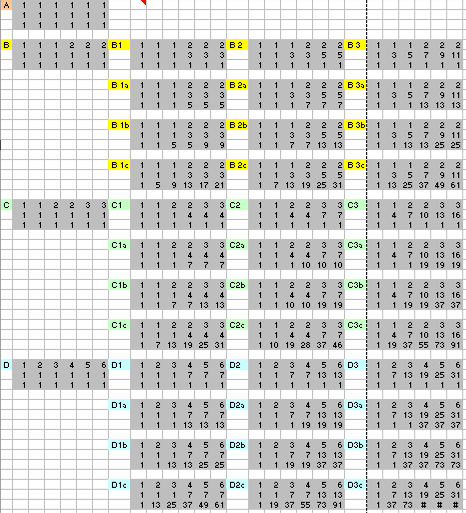
WONDERP ha individuato un numero di dadi di poco inferiore (40 terne) con metodi intuitivi. Ecco la sua soluzione.
Le soluzioni sono (variando il primo dado):
a 1,1,1 (i tre dadi tutti con 1)
b (1,2),1,1 (il primo dado con tre 1 e tre 2, gli altri tutti 1)
c (1,2,3),1,1 (il primo dado con due 1, due 2 e due 3, gli altri tutti 1)
d (1,2,3,4,5,6),1,1 (il primo dado con numeri da 1 a 6 gli altri tutti 1)
come si può vedere b e c sono un sottoinsieme di d. Per ora ho 1+3=4 soluzioni (spiego dopo perché scrivo 1+3).
Il primo dado non può variare in altro modo.
Dalla soluzione b, variando il secondo dado e risulta
(1,2),(1,3),1
(1,2),(1,3,5),1
(1,2),(1,3,5,7,9,11),1
altre 3 soluzioni ed anche questa volta le prime due possono essere dedotte dalla terza.
Quindi posso scrivere ogni volta solo la terza, ad esempio continuando il caso c scrivo:
(1,2,3),(1,4,7,10,13,16),1
per d:
(1..6),(1,7,13,19,25,31),1
sempre tre casi.
Quindi le soluzioni sono 1+3+9=3^0+3^1+3^2=13, posso continuare per analogia e dire che il numero totale di soluzioni sono 1+3+9+27=40
faccio qualche esempio dell’ultimo passaggio, vario cioè il terzo dado, da (1,2),(1,3),1 scritta sopra posso ricavare
(1,2),(1,3),(1,5)
(1,2),(1,3),(1,5,9)
(1,2),(1,3),(1,5,9,13,17,21)
per ricavare questa serie non ho fatto altro che sommare i numeri maggiori
scritti sui primi due dadi, nel nostro caso 2+3=5 che è il secondo termine
del terzo dado (il primo è obbligatoriamente 1) e poi proseguo con una successione,
cioè 1(+4) 5(+4) 9(+4) 13(+4) 17(+4) 21. Quindi, ricapitolando, da 1 ne ricavo 3, da 3 ne ricavo 9, da nove ne ricavo 27.
Per fare un un ultimo esempio:
(1,2,3,4,5,6),(1,7,13,19,25,31),(1,37,73,109,145,181)
con questi dadi posso ottenere tutti i numeri da 3 a 218 con possibilità di uscire 1/216.
Ecco tutte le soluzioni di WONDERP