Coefficiente binomiale
Dati $n, k in mathbb{N}$, con $n ge k$, si definisce coefficiente binomiale di $n$ su $k$
$((n),(k)) = frac{n!}{k! (n-k)!}$
Esempio: $((4),(2)) = frac{4!}{2! (4-2)!} = frac{4!}{2! cdot 2!} = frac{4 cdot 3 cdot 2 cdot 1}{2 cdot 1 cdot 2 cdot 1} = 6$
Proprietà del coefficiente binomiale
I coefficienti binomiali rispettano le seguenti proprietà
$((n),(0)) = ((n),(n)) = 1 quad forall n in mathbb{N}$
$((n),(1)) = ((n),(n – 1)) = n quad forall n in mathbb{N}$
$((n),(k)) = ((n),(n-k)) quad forall n,k in mathbb{N}$, $n ge k$
$((n+1),(k+1)) = ((n),(k+1)) + ((n),(k)) quad forall n,k in mathbb{N}$, $n ge k$
$sum_{k=0}^n ((n),(k)) a^k b^{n-k} = (a+b)^n$
In particolare, dall’ultima proprietà discende che
$sum_{k=0}^n ((n),(k)) = 2^n quad forall n in mathbb{N}$
Coefficiente multinomiale
Dati $r+1$ numeri naturali, $n, k_1, k_2, ldots, k_r in mathbb{N}$, tali che $k_1 + k_2 + ldots + k_r = n$, si definisce coefficiente multinomiale
$((n),(k_1"," k_2"," ldots"," k_r)) = frac{n!}{k_{1}! cdot k_{2}! cdot ldots cdot k_{r}!} = frac{n!}{prod_{i=1}^r k_{i}!}$
e comunque si scelgano i numeri naturali $n, k_1, k_2, ldots, k_r$ (purché $k_1 + k_2 + ldots + k_r = n$), risulta
$((n),(k_1"," k_2"," ldots"," k_r)) in mathbb{N}$
Proprietà del coefficiente multinomiale
Fissato $n in mathbb{N}$, e detto $A_n subset mathbb{N}^r$ l’insieme di tutte le $r$-ple di naturali $(k_1, k_2, ldots, k_r)$ tali che $k_1 + k_2 + ldots + k_r = n$, risulta
$(x_1 + x_2 + ldots + x_r)^n = sum_{(k_1, k_2, ldots, k_r) in A_n} ((n),(k_1"," k_2"," ldots"," k_r)) cdot x_1^{k_1} cdot x_2^{k_2} cdot ldots cdot x_r^{k_r}$
Permutazioni semplici
Dato un insieme $X$ con $n$ elementi, si chiama permutazione ogni ordinamento dell’insieme $X$. Equivalentemente, dati $n$ oggetti distinti, il numero di permutazioni $P_n$ è il numero di tutti i possibili ordinamenti degli $n$ oggetti, e risulta
$P_n = n!$
Esempio: in quanti modi diversi si possono disporre $10$ persone in fila? Risposta: $10!$
Permutazioni con ripetizione
Dati $n$ oggetti non tutti distinti fra di loro, un ordinamento di tali oggeti si chiama permutazione con ripetizione. Supponiamo di poter suddividere gli $n$ oggetti in $h$ tipi diversi (ovviamente $h le n$). Siano $n_i$ il numero di elementi di tipo $i$, per ogni $i=1, 2, ldots, h$, allora $n = n_1 + n_2 + ldots + n_h$. Indicando con $P_{n_1, n_2, ldots, n_h}^{**}$ il numero delle permutazioni con ripetizione, ovvero il numero di tutti i possibili ordinamenti degli $n$ oggetti, risulta
$P_{n_1, n_2, ldots, n_h}^{**} = frac{n!}{n_{1}! cdot n_{2}! cdot ldots cdot n_{h}!}$
Esempio: Quanti sono i possibili anagrammi della parola matematica?
Si hanno in totale $10$ elementi, visto che la parola matematica è costituita da $10$ lettere. Tali lettere non sono tutte distinte, ma possono essere partizionate in $6$ tipi diversi
1° tipo: lettera m, $n_1 = 2$
2° tipo: lettera a, $n_2 = 3$
3° tipo: lettera t, $n_3 = 2$
4° tipo: lettera e, $n_4 = 1$
5° tipo: lettera i, $n_5 = 1$
6° tipo: lettera c, $n_6 = 1$
Per determinare il numero di tutti i possibili anagrammi della parola matematica basta calcolare le permutazioni con ripetizione
$frac{10!}{2! cdot 3 ! cdot 2! cdot 1! cdot 1! cdot 1!} = 10 cdot 9 cdot 8 cdot 7 cdot 6 cdot 5 = 151200$
Combinazioni semplici
Dato un insieme $X$ con cardinalità $n$ (quindi contenente $n$ elementi distinti), ogni sottoinsieme di $X$ con $k$ elementi ($0 le k le n$) viene detto combinazione di $n$ oggetti di classe $k$, e si indica con $C_{n,k}$.
$C_{n,k}$ rappresenta il numero di tutti possibili modi con cui si possono scegliere $k$ elementi fra $n$ oggetti dati, e risulta
$C_{n,k} = ((n),(k)) = frac{n!}{k! (n-k)!}$
ed inoltre
$C_{n,k} = frac{n!}{k! (n-k)!} = P_{k, n-k}^{**}$
Esempio: Quanti sono i possibili sottoinsiemi di un insieme $n$ elementi? I possibili sottoinsiemi possono essere l’insieme vuoto, gli insiemi con $1$ elemento, gli insiemi con $2$ elementi, etc. Quindi il numero di tutti i possibili sottoinsiemi è
$sum_{k=0}^n ((n),(k)) = 2^n$
Combinazioni con ripetizione
Dato un insieme $X$ di cardinalità $n$, ossia dati $n$ oggetti distinti, ogni raggruppamento di $k$ elementi di $X$, ammettendo anche ripetizioni di oggetti, viene detto combinazione con ripetizione di $n$ oggetti di classe $k$. Notare che $k$ può essere maggiore di $n$, e in ogni raggruppamento non conta l’ordine con cui vengono elencati gli elementi. Indicando con $C_{n,k}^{**}$ il numero di tutte le possibili combinazioni con ripetizione di $n$ oggetti di classe $k$, risulta
$C_{n,k}^{**} = ((n+k-1),(k))$
Esempio: Dato $X = {a, b, c, d}$, quante sono le possibili coppie formate da elementi di $X$, ammettendo anche ripetizioni, senza contare l’ordine con cui tali elementi sono elencati? Risposta: $C_{4,2} = ((4+2-1),(2)) = ((5),(2)) = 10$. E infatti tutte le coppie possibili sono
Esempio: In quanti modi si possono scegliere $5$ carte da un mazzo di $40$ con rimpiazzo? Risposta: $C_{40,5}^{**} = ((40 + 5 – 1),(5)) = ((44),(5))$
Disposizioni semplici
Dati $n$ oggetti, ogni ordinamento di $k$ oggetti ($0 le k le n)$ comunque scelti fra gli $n$ si chiama disposizione di $n$ oggetti di classe $k$. Notare che due disposizioni possono differire o per gli oggetti contenuti o per l’ordine degli oggetti. Il numero di tutte le possibili disposizioni di $n$ oggetti di classe $k$ si indica con $D_{n,k}$ e risulta
$D_{n,k} = frac{n!}{(n-k)!} = n cdot (n-1) cdot ldots cdot (n-k+1)$
Esempio: Da un’urna contenente $90$ palline numerate, quante sono le possibili sequenze di $5$ numeri che si possono ottenere estraendo, senza rimpiazzo, cinque palline? Risposta: $D_{90,5} = frac{90!}{85!}$
Disposizioni con ripetizione
Dati $n$ oggetti, ogni ordinamento di $k$ oggetti in cui sono ammesse anche ripetizioni (quindi $k$ può essere qualsiai) si chiama disposizione con ripetizione di $n$ oggetti di classe $k$. Indicando con $D_{n,k}^{**}$ il numero di tutte le possibili disposizioni con ripetizioni di $n$ oggetti di classe $k$, risulta
$D_{n,k}^{**} = n^k$
Esempio: Da un’urna contenente $90$ palline numerate, quante sono le possibili sequenze di $5$ numeri che si possono ottenere estraendo, con rimpiazzo, cinque palline? Risposta: $D_{90,5}^{**} = 90^5$
Esempio: quante sono le parole di $4$ lettere che si possono formare utilizzando le lettere ${a,b,c,d,e}$? Risposta: $D_{5,4}^{**} = 5^4$.

 Tutto sugli insiemi, tutte (o quasi) le formule che bisogna conoscere e che si possono incontrare: Generalità, Relazioni e operazioni, Funzione, Strutture algebriche.
Tutto sugli insiemi, tutte (o quasi) le formule che bisogna conoscere e che si possono incontrare: Generalità, Relazioni e operazioni, Funzione, Strutture algebriche.  Formulario sugli insiemi numerici: Proprietà delle quattro operazioni, Numeri primi e divisibilità, Numeri primi da 1 a 10000, Massimo comune divisore e minimo comune multiplo, Frazioni e numeri razionali, Assiomatizzazione degli insiemi numerici, Valore assoluto, Funzione segno, Parte intera, Approssimazione, Fattoriale.
Formulario sugli insiemi numerici: Proprietà delle quattro operazioni, Numeri primi e divisibilità, Numeri primi da 1 a 10000, Massimo comune divisore e minimo comune multiplo, Frazioni e numeri razionali, Assiomatizzazione degli insiemi numerici, Valore assoluto, Funzione segno, Parte intera, Approssimazione, Fattoriale.  Formulario completo di geometria piana, tutte le formule e tutti i teoremi più importanti. Rettangolo, quadrato, parallelogramma, triangolo, rombo, deltoide, trapezio, poligoni regolari, circonferenza, cerchio, settore circolare, corona circolare, triangolo inscritto e circoscritto a un cerchio, poligono inscritto e circoscritto, tutte le definizioni e i teoremi di geometria piana.
Formulario completo di geometria piana, tutte le formule e tutti i teoremi più importanti. Rettangolo, quadrato, parallelogramma, triangolo, rombo, deltoide, trapezio, poligoni regolari, circonferenza, cerchio, settore circolare, corona circolare, triangolo inscritto e circoscritto a un cerchio, poligono inscritto e circoscritto, tutte le definizioni e i teoremi di geometria piana.  5.1. Unità di misura del Sistema Internazionale (SI) – Grandezze fondamentali – Grandezze supplementari – 5.2. Multipli e sottomultipli del Sistema Internazionale – 5.3. Principali grandezze derivate – Meccanica – Elettromagnetismo – 5.4. Principali unità di misura che non appartengono al SI – 5.5. Intervalli di variabilità di alcune unità fondamentali – Lunghezze – Tempi – Masse – Temperature – 5.6. Costanti fisiche.
5.1. Unità di misura del Sistema Internazionale (SI) – Grandezze fondamentali – Grandezze supplementari – 5.2. Multipli e sottomultipli del Sistema Internazionale – 5.3. Principali grandezze derivate – Meccanica – Elettromagnetismo – 5.4. Principali unità di misura che non appartengono al SI – 5.5. Intervalli di variabilità di alcune unità fondamentali – Lunghezze – Tempi – Masse – Temperature – 5.6. Costanti fisiche.  Formulario completo di geometria solida: parallelepipedo, cubo, prisma, piramide, tronco di piramide, poliedri regolari, cilindro, cono, tronco di cono, sfera, calotta sferica e segmento sferico a una base, settore sferico, zona sferica e segmento sferico a due basi, fuso sferico o spicchio sferico, cilindro a sezione obliqua, corona cilindrica, obelisco, cuneo, toro, prisma obliquo triangolare.
Formulario completo di geometria solida: parallelepipedo, cubo, prisma, piramide, tronco di piramide, poliedri regolari, cilindro, cono, tronco di cono, sfera, calotta sferica e segmento sferico a una base, settore sferico, zona sferica e segmento sferico a due basi, fuso sferico o spicchio sferico, cilindro a sezione obliqua, corona cilindrica, obelisco, cuneo, toro, prisma obliquo triangolare.  Definizione di proporzione, proprietà delle proporzioni, risolvere una proporzione, grandezze direttamente e inversamente proporzionali, problemi con le proporzioni, problemi del tre semplice e problemi del tre composto, percentuali, problemi con le percentuali, problemi con gli sconti, problemi di cambio di moneta.
Definizione di proporzione, proprietà delle proporzioni, risolvere una proporzione, grandezze direttamente e inversamente proporzionali, problemi con le proporzioni, problemi del tre semplice e problemi del tre composto, percentuali, problemi con le percentuali, problemi con gli sconti, problemi di cambio di moneta.  7.1 Definizione di potenza – 7.2 Proprietà delle potenze – 7.4 Proprietà delle radici – 7.5 Razionalizzazione del denominatore – 7.6 Radicali doppi
7.1 Definizione di potenza – 7.2 Proprietà delle potenze – 7.4 Proprietà delle radici – 7.5 Razionalizzazione del denominatore – 7.6 Radicali doppi 
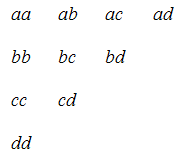
 Il capitolo 12 del Formulario di matematica, un formulario completo da stampare e consultare su tutti gli argomenti. In questo capitolo il calcolo letterale: 1. espressioni letterali – 2. Prodotti notevoli – 3. Scomposizione in fattori – raccoglimento a fattor comune totale, raccoglimento parziale, quadrato di binomio, cubo di binomio, differenza di quadrati, differenza di cubi, somma di cubi, differenza di potenze di uguale esponente,trinomio caratterestico.
Il capitolo 12 del Formulario di matematica, un formulario completo da stampare e consultare su tutti gli argomenti. In questo capitolo il calcolo letterale: 1. espressioni letterali – 2. Prodotti notevoli – 3. Scomposizione in fattori – raccoglimento a fattor comune totale, raccoglimento parziale, quadrato di binomio, cubo di binomio, differenza di quadrati, differenza di cubi, somma di cubi, differenza di potenze di uguale esponente,trinomio caratterestico.