Scratch consente di programmare il computer per risolvere problemi e creare simulazioni, animazioni, storie interattive, grafica. In pratica usa dei mattoncini simili al Lego o ai pezzi del puzzle (gli Scratch blocks ➔ blocchi) per costruire progetti multimediali che mettono assieme immagini, suoni, video ecc.
La codifica dei programmi in Scratch consiste nell’impilare, incastrandoli, oggetti grafici che presentano forma e colore dipendenti dall’istruzione che si vuole usare.
All’apertura del programma si presenta questa schermata:

Nel frame di sinistra si vedono i comandi veri e propri suddivisi per categorie:

Tali comandi possono essere trascinati nell’area centrale (Script) dove possono essere direttamente eseguiti con un click sul comando stesso.
Tale esecuzione si osserva nel riquadro a destra: lo stage. Il protagonista è lo sprite (nel nostro caso il gatto) che visualizza l’esecuzione dei comandi.
Sopra lo stage, sulla sinistra, si vedono 4 pulsanti utili: Duplica, Cancella, Espandi sprite, Riduci sprite

Per cancellare o duplicare il comando, trascinato nell’area di Script, si può anche ricorrere al menù contestuale che appare alla pressione del tasto destro del mouse sul comando stesso.
Es1
 Clicchiamo su “fai 10 passi” e trasciniamolo nella pagina degli Script (quella al centro). Cliccando su 10 possiamo inserire il valore 100. Facciamo spostare il gatto cliccando sulla parola passi del blocco. Cliccando sul gatto, possiamo trascinarlo in un’altra posizione e farlo muovere di nuovo. Eliminiamo il blocco trascinandolo nella sezione dei blocchi (oppure tasto destro sul blocco e scegliere Cancella).
Clicchiamo su “fai 10 passi” e trasciniamolo nella pagina degli Script (quella al centro). Cliccando su 10 possiamo inserire il valore 100. Facciamo spostare il gatto cliccando sulla parola passi del blocco. Cliccando sul gatto, possiamo trascinarlo in un’altra posizione e farlo muovere di nuovo. Eliminiamo il blocco trascinandolo nella sezione dei blocchi (oppure tasto destro sul blocco e scegliere Cancella).
Es2
Inseriamo ora una serie di blocchi dopo aver spostato lo sprite nella parte sinistra dello stage. Cliccando poi sul blocco passi otteniamo il movimento.
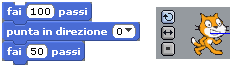 Dopo aver eseguito i comandi possiamo far ritornare lo sprite alla posizione iniziale facendo doppio clic sul gatto posto al di sopra dello Script.
Dopo aver eseguito i comandi possiamo far ritornare lo sprite alla posizione iniziale facendo doppio clic sul gatto posto al di sopra dello Script.
Es3
Dopo aver tolto i due blocchi inferiori lasciando il solo blocco “fai 100 passi”, aggiungiamo un suono. Scegliamo la categoria Suono ➔ Produci suono miao e attendi la fine. Lanciamo il programma.
Es4
 Dopo aver tolto il blocco del suono, inseriamo i seguenti blocchi regolando il numero delle battute, il tipo di suono. Nel secondo blocco fai passi inserire il numero -100 per farlo tornare alla partenza.
Dopo aver tolto il blocco del suono, inseriamo i seguenti blocchi regolando il numero delle battute, il tipo di suono. Nel secondo blocco fai passi inserire il numero -100 per farlo tornare alla partenza.
Es5
 Dalla categoria Controllo prendiamo “ripeti 5 volte” e trasciniamolo nello Script. Avvicinandolo agli altri blocchi noteremo che questo si allarga: una volta che li ha contenuti tutti, rilasciamo il pulsante del mouse. Cliccare infine su un blocco per azionare il programma. Rifarlo quindi facendolo ripetere 10 volte. Per eliminare il controllo giallo cliccare sul blocco fai 100 passi e trascinare in basso. Trascinare il blocco ripeti nella parte dei comandi e scegliere “Per sempre” attaccandolo agli altri blocchi. Lanciare il programma; per fermare il tutto cliccare sul pulsante rosso (ferma tutto) posto al di sopra dello Stage.
Dalla categoria Controllo prendiamo “ripeti 5 volte” e trasciniamolo nello Script. Avvicinandolo agli altri blocchi noteremo che questo si allarga: una volta che li ha contenuti tutti, rilasciamo il pulsante del mouse. Cliccare infine su un blocco per azionare il programma. Rifarlo quindi facendolo ripetere 10 volte. Per eliminare il controllo giallo cliccare sul blocco fai 100 passi e trascinare in basso. Trascinare il blocco ripeti nella parte dei comandi e scegliere “Per sempre” attaccandolo agli altri blocchi. Lanciare il programma; per fermare il tutto cliccare sul pulsante rosso (ferma tutto) posto al di sopra dello Stage.
Es6
 Sulla struttura precedente inseriamo in cima il blocco “quando si clicca su”. Cliccare sullo stesso per farlo partire e poi per fermarlo da pulsante rosso.
Sulla struttura precedente inseriamo in cima il blocco “quando si clicca su”. Cliccare sullo stesso per farlo partire e poi per fermarlo da pulsante rosso.
Es7
 Sotto al precedente blocco inseriamo il Controllo “quando si preme il tasto spazio” e l’Aspetto “cambia effetto colore di 25”. Lanciare il programma e premere in successione la barra spaziatrice. Provare quindi a cambiare l’effetto, sostituendo colore con fish-eye o altri.
Sotto al precedente blocco inseriamo il Controllo “quando si preme il tasto spazio” e l’Aspetto “cambia effetto colore di 25”. Lanciare il programma e premere in successione la barra spaziatrice. Provare quindi a cambiare l’effetto, sostituendo colore con fish-eye o altri.
Es8
 Nella sezione Nuovo sprite, cliccare su Seleziona nuovo sprite da file, scegliere People (2 clic) e prendere jodi1 e cancellare il gatto. Scegliamo quindi la categoria Aspetto e prendiamo il blocco Dire ciao! per 1 secondo.
Nella sezione Nuovo sprite, cliccare su Seleziona nuovo sprite da file, scegliere People (2 clic) e prendere jodi1 e cancellare il gatto. Scegliamo quindi la categoria Aspetto e prendiamo il blocco Dire ciao! per 1 secondo.

Inseriamo quindi gli altri blocchi e proviamo a cambiare i tempi del saluto e l’effetto colore.

Per tornare alla situazione di partenza cliccare sul pulsante Ferma tutto (rosso). Inseriamo infine il blocco Ripeti 5 volte e proviamo.
Es9
Dopo aver eliminato lo sprite gatto, scegliere un nuovo sprite ➔ Jodi1. Aprire la scheda Costumi, cliccare su Importa e scegliere jodi2. Ritorniamo alla finestra Script ed inseriamo dalla categoria Aspetto il blocco Passa al costume seguente e dalla categoria Controllo i blocchi “attendi 1 secondo” e “per sempre”. Lanciare il programma. Cambiare poi il tempo di attesa (0,5 s)

Es 10
Dopo aver eliminato lo sprite gatto, scegliere un nuovo sprite ➔ breakdancer-1. Aprire la scheda Costumi,

cliccare su Importa e scegliere breakdancer-2, ripetere con breakdancer-3 e breakdancer-4. Ritorniamo alla finestra Script ed inseriamo dalla categoria Aspetto il blocco Passa al costume seguente e dalla categoria Controllo i blocchi “attendi 0,5 secondi” e “Ripeti 10 volte”. Lanciare il programma.

Es11
Provare con ballerina (4 costumi) boy-walking(4 coatumi) e dan (6 costumi).
Es12
Inserire lo sprite Elicopter1 dalla categoria Trasportation. Ridurre le dimensioni cliccando sullo sprite dopo aver scelto l’icona Riduci sprite (cliccare poi in un punto qualsiasi per deselezionarla).

Lanciare il programma.
Es13
Dopo aver scelto File ➔ Nuovo, Inserire le seguenti righe di comando:

Lanciare il programma.
Es14 Animazione semplice
Dopo aver ridotto le dimensioni dello sprite, dalla scheda Costumi importare Cat1-b e inserire nello script i comandi riportati. Lanciare il programma.

Es15
Ripetere (dopo aver cancellato il gatto) inserendo lo sprite bat1-a ed il costume bat1-b (ridurre le dimensioni dello sprite). Inserire lo script precedente poi cliccare su Stage (in basso a destra) per mettere uno sfondo (da Sfondi ➔ Importa ➔ Nature ➔ Desert).
Nota: per copiare lo script procedere così: inserire il nuovo sprite bat1-a, cliccare quindi col tasto destro sopra allo script e scegliere Dupluica. Trascinare la copia sopra all’icona di bat1-a (in basso a destra) e rilasciare.

Ripetere con altri animali, cambiando anche lo sfondo.
Es16
 Cancellare il gatto e inserire lo sprite (da Things) Trampoline. Inserire quindi l’altro sprite (da Animals) duck1, cliccandoci sopra più volte per rimpiccolirlo (dopo aver preso Riduci sprite) e inserirlo sopra a trampoline. Digitare lo script riportato. Nota: quando si inserisce il blocco produci suono, cliccare sulla freccetta e poi su registra.. quindi su annulla e infine su importa ➔ Animal ➔ Duck ➔ Ok.
Cancellare il gatto e inserire lo sprite (da Things) Trampoline. Inserire quindi l’altro sprite (da Animals) duck1, cliccandoci sopra più volte per rimpiccolirlo (dopo aver preso Riduci sprite) e inserirlo sopra a trampoline. Digitare lo script riportato. Nota: quando si inserisce il blocco produci suono, cliccare sulla freccetta e poi su registra.. quindi su annulla e infine su importa ➔ Animal ➔ Duck ➔ Ok.
Per creare uno sfondo cliccare su Stage (basso a destra) e poi su Sfondi (alto a sinistra) quindi su Importa ➔ Nature ➔ beach-malibu.

Es17
Ping pong
Cancellare il gatto e disegnare lo sprite racchetta (rac1), cliccare quindi su di esso e scegliere Duplica (rac2). Disegnare infine lo sprite Pallina (cerchio rosso). Cliccare su Script e digitare:
| Rac1 |
Rac2 |
 |
 |
Pallina
Lo sfondo si ottiene cliccando su Stage ➔ Disegna. Può essere fatto a piacere (es. bianco o colorato, non dello stesso colore delle racchette).


Es18 sistema solare
Importare gli sprite da Scartch (Luna, Giove, Terra e Sole). Inserire lo sfondo (Importa ➔ Nature ➔ stars). Digitare i seguenti script, poi lanciare il programma.

Es19 labirinto
Realizzare lo sprite a forma di pallina, quindi lo sfondo tipo quello che si vede in figura. Inserire gli script:

Es20
 Dopo aver cancellato il gatto, inserire da Letters ➔ Funky gli sprite C, A, N ed E . Dopo aver realizzato lo script per la lettera A, cliccare sulla stessa col tasto destro, scegliere duplica e trascinare la copia sopra allo sprite con la lettere B (in basso a destra) e ripetere per le altre due lettere, in modo da copiare lo stesso script..
Dopo aver cancellato il gatto, inserire da Letters ➔ Funky gli sprite C, A, N ed E . Dopo aver realizzato lo script per la lettera A, cliccare sulla stessa col tasto destro, scegliere duplica e trascinare la copia sopra allo sprite con la lettere B (in basso a destra) e ripetere per le altre due lettere, in modo da copiare lo stesso script..
Cliccare sulla bandierina verde per farli partire assieme. Provare a cambiare il verso delle rotazioni e poi gli angoli di rotazione per ottenere maggiore o minor velocità della rotazione stessa. Cliccare sulla bandierina verde per far partire l’animazione.
Es21
Cancellare il gatto ed inserire gli sprite Airplane e yacht da Transportation. Realizzare lo sfondo da Importa ➔ Outdoors ➔ city with water. Posizionare gli sprite e inserire gli script:
 |
Per lo yatch
Copiare quello dell’aereo cambiando solo “fai 1 passo”. |
Es22 danza
Dopo aver eliminato il gatto inserire lo sprite ballerina-a da People. Cliccare quindi su Costumi ed importare le altre tre ballerine b, c e d). Inserire quindi lo sfondo spotligth-stage da Indoors. Scrivere quindi i seguenti script. Cliccare sulla bandierina verde per far partire l’animazione. Cliccare sulla bandierina verde.

Es23
Dopo aver inserito lo script:

Muovere il mouse portandolo vicino al gatto. Se la distanza è minore di 10, sentiremo il gatto miagolare.
Es24 Vari effetti sugli sprite
Dopo aver cancellato il gatto, inserire gli sprite da Animals, butterfly3 Elephant1-a (per questo inserire anche il costume elephant1-b) e duck1. Digitare quindi i seguenti script, poi lanciare il programma.
| Butterfly3 |
Elephant1-a |
Duck1 |
 |
 |
 |
Es25 palla labirinto
Dopo aver eliminato il gatto, inserire da Things ➔ baseball1, quindi creare lo sfondo simile a quello in figura. Digitare gli script indicati, poi lanciare il programma.

Es26
Dopo aver eliminato il gatto, realizzare uno sprite rettangolare nero e duplicarlo 5 volte (cliccarci sopra col tasto destro e scegliere Duplica). Realizzare uno sprite rettangolare più grande e riempirlo di un colore avorio; duplicarlo 8 volte e posizionare il tutto come in figura:

Digitare i seguenti script:
| Tasto nero (copiare lo script e poi aggiustare il valore) |
Tasto bianco |

Il primo valore 61 si riferisce al primo sprite da sinista, gli altri valori sono 63, 66, 68 e 70 |

Il primo valore 60 si riferisce al primo sprite da sinista, gli altri valori sono 62, 64, 65, 67, 69, 71 e 72 |
Poi lanciare il programma a tutto schermo e suonare.
TEOREMA ANGOLO ESTERNO: consideriamo una matita e con la punta facciamogli percorrere tutti i lati esterni di un poligono. Qualunque sia il numero dei lati la matita percorre sempre un angolo giro (360°). Per seguire il contorno di un quadrato dovrà ruotare 4 volte e ogni rotazione sarà di 360 : 4 = 90°. Per un pentagono avremo 360 : 5 = 72°….. per un decagono 360 : 10 = 36°.

Es27 disegno quadrato
Dopo aver digitato lo script, lanciare il programma.

Otteniamo una serie di quadrati con il seguente script. Se l’angolo è di 30° devo ripetere 12 volte (per avere un giro completo). Quanto devo Ripetere per un angolo di 60°?
Allunghiamo lo script inserendo gli ulteriori blocchi indicati.

Es28 disegno rettangolo
Dopo aver digitato lo script, lanciare il programma.

Es29 disegno triangolo equilatero
Dopo aver digitato lo script, lanciare il programma.

Es30 disegno pentagono
Dopo aver digitato lo script, lanciare il programma.

Es31 disegno esagono
Dopo aver digitato lo script, lanciare il programma.

Es32 disegno decagono
Dopo aver digitato lo script, lanciare il programma.

Es33 vari rettangoli
Dopo aver digitato lo script, lanciare il programma.

Disegnare una serie di 4 quadrati di lato 80.
Es34 stella (digitare lo script e lanciare)
|
Es35 stella1 (digitare lo script e lanciare)
|
 |
 |
Es36 stella2
Dopo aver digitato lo script, lanciare il programma.

Es37 stella3
Dopo aver digitato lo script, lanciare il programma.

Es38 circonferenza
Dopo aver digitato lo script, lanciare il programma.

Es39 stella4
Dopo aver digitato lo script, lanciare il programma.

Es40 grechina
Dopo aver digitato lo script, lanciare il programma.

Es41
Dopo aver inserito gli sprite Crab-1, Dinosaur1 e Lion1-a, digitare i seguenti script. Si otterranno 4 poligoni.
| Gatto |
Crab-1 |
Dinosaur1 |
Lion1-a |
 |
 |
 |
 |
Es42 dialogo1
Dopo aver digitato lo script, lanciare il programma.

Provare a realizzare un dialogo a vostro piacimento.
Es43 dialogo1
Dopo aver digitato lo script, lanciare il programma.

Es44 dialogo lungo
Script del primo sprite:

Script del secondo sprite:

Es45 versi degli animali
Dopo aver cancellato il gatto, inserire gli sprite cat1-a, duck1 e horse1-a digitare gli script, e lanciare il programma.

Es46 disegno poligono qualsiasi
Dopo aver digitato lo script, lanciare il programma.

Es47 poligono regolare
Lo sfondo si ottiene da Stage ➔ Importa ➔ xy-grid

La penultima riga si ottiene seguendo la costruzione indicata:

Es 48 spirale quadrato
Dopo aver digitato lo script, lanciare il programma.

Es 49 spirale

Es 50 spirale quadrata
Dopo aver digitato lo script, lanciare il programma.

Es 51 spirale 2
Dopo aver digitato lo script, lanciare il programma.

Es52 vari poligoni

Es53 area del quadrato
Dopo aver digitato lo script, lanciare il programma.

Es54 perimetro del quadrato
Dopo aver digitato lo script, lanciare il programma.

Es55 area del rettangolo
Dopo aver digitato lo script, lanciare il programma.

Es56 perimetro del rettangolo
Dopo aver digitato lo script, lanciare il programma.

Es57 media aritmetica tra due numeri
Dopo aver digitato lo script, lanciare il programma.

Es 58 Palla che si muove
Dopo aver cancellato il gatto, inserire da Things ➔ soccer1. Realizzare quindi uno sfondo (Stage ➔ Sfondi ➔ Disegna) tipo quello indicato.

Dopo aver digitato gli script, lanciare il programma.


Es59 acquario
Dopo aver cancellato il gatto, inserire gli sprite Fish2, fish3 e fish4. Inserire quindi lo sfondo (Stage ➔ Importa ➔ Nature ➔ Underwater).Dopo aver digitato lo script, lanciare il programma.

Es60 acquario con squalo
Dopo aver cancellato il gatto ed aver inserito gli sprite (da Animals) Fish2 e scark1-b, inserire lo sfondo (Stage ➔ Importa ➔ Nature ➔ Underwater). Digitare quindi gli script seguenti:

Script squalo






 Dopo aver eseguito i comandi possiamo far ritornare lo sprite alla posizione iniziale facendo doppio clic sul gatto posto al di sopra dello Script.
Dopo aver eseguito i comandi possiamo far ritornare lo sprite alla posizione iniziale facendo doppio clic sul gatto posto al di sopra dello Script. Dopo aver tolto il blocco del suono, inseriamo i seguenti blocchi regolando il numero delle battute, il tipo di suono. Nel secondo blocco fai passi inserire il numero -100 per farlo tornare alla partenza.
Dopo aver tolto il blocco del suono, inseriamo i seguenti blocchi regolando il numero delle battute, il tipo di suono. Nel secondo blocco fai passi inserire il numero -100 per farlo tornare alla partenza. Dalla categoria Controllo prendiamo “ripeti 5 volte” e trasciniamolo nello Script. Avvicinandolo agli altri blocchi noteremo che questo si allarga: una volta che li ha contenuti tutti, rilasciamo il pulsante del mouse. Cliccare infine su un blocco per azionare il programma. Rifarlo quindi facendolo ripetere 10 volte. Per eliminare il controllo giallo cliccare sul blocco fai 100 passi e trascinare in basso. Trascinare il blocco ripeti nella parte dei comandi e scegliere “Per sempre” attaccandolo agli altri blocchi. Lanciare il programma; per fermare il tutto cliccare sul pulsante rosso (ferma tutto) posto al di sopra dello Stage.
Dalla categoria Controllo prendiamo “ripeti 5 volte” e trasciniamolo nello Script. Avvicinandolo agli altri blocchi noteremo che questo si allarga: una volta che li ha contenuti tutti, rilasciamo il pulsante del mouse. Cliccare infine su un blocco per azionare il programma. Rifarlo quindi facendolo ripetere 10 volte. Per eliminare il controllo giallo cliccare sul blocco fai 100 passi e trascinare in basso. Trascinare il blocco ripeti nella parte dei comandi e scegliere “Per sempre” attaccandolo agli altri blocchi. Lanciare il programma; per fermare il tutto cliccare sul pulsante rosso (ferma tutto) posto al di sopra dello Stage. Sulla struttura precedente inseriamo in cima il blocco “quando si clicca su”. Cliccare sullo stesso per farlo partire e poi per fermarlo da pulsante rosso.
Sulla struttura precedente inseriamo in cima il blocco “quando si clicca su”. Cliccare sullo stesso per farlo partire e poi per fermarlo da pulsante rosso. Sotto al precedente blocco inseriamo il Controllo “quando si preme il tasto spazio” e l’Aspetto “cambia effetto colore di 25”. Lanciare il programma e premere in successione la barra spaziatrice. Provare quindi a cambiare l’effetto, sostituendo colore con fish-eye o altri.
Sotto al precedente blocco inseriamo il Controllo “quando si preme il tasto spazio” e l’Aspetto “cambia effetto colore di 25”. Lanciare il programma e premere in successione la barra spaziatrice. Provare quindi a cambiare l’effetto, sostituendo colore con fish-eye o altri.















 Dopo aver cancellato il gatto, inserire da Letters ➔ Funky gli sprite C, A, N ed E . Dopo aver realizzato lo script per la lettera A, cliccare sulla stessa col tasto destro, scegliere duplica e trascinare la copia sopra allo sprite con la lettere B (in basso a destra) e ripetere per le altre due lettere, in modo da copiare lo stesso script..
Dopo aver cancellato il gatto, inserire da Letters ➔ Funky gli sprite C, A, N ed E . Dopo aver realizzato lo script per la lettera A, cliccare sulla stessa col tasto destro, scegliere duplica e trascinare la copia sopra allo sprite con la lettere B (in basso a destra) e ripetere per le altre due lettere, in modo da copiare lo stesso script..