 |
Test sullo Sviluppo in Serie di Potenze delle Funzioni Irrazionali |
 |
Test sullo Sviluppo in Serie di Potenze delle Funzioni Irrazionali |
 La tesina di astronomia sulla materia oscura che ha vinto il primo premio nel concorso "Premio Maturità 2007". Questa tesina di maturità scientifica presenta le ricerche di astrofisica relative alla materia oscura dal 1933 al 2007.
La tesina di astronomia sulla materia oscura che ha vinto il primo premio nel concorso "Premio Maturità 2007". Questa tesina di maturità scientifica presenta le ricerche di astrofisica relative alla materia oscura dal 1933 al 2007.
La ricerca astronomica della materia oscura: dal 1933 al 2007. Prove sperimentali e accenni teorici
Con una piccola digressione filosofica e citazioni letterarie (italiane e inglesi) e artistiche sparse
Dalla premessa
Personalmente mi sento molto affascinato dalla volta celeste, con ciò che mostra e ciò che invece ancora nasconde. Il cielo non è altro che la testimonianza presente del mistero in cui l’uomo è immerso. Sviluppando questa mia passione per l’astronomia e il fascino per l’ignoto proprio di tutti noi, ho scelto di trattare di uno dei grandi misteri che nemmeno la scienza più moderna riesce a comprendere nella sua pienezza. La materia oscura ha una cruciale importanza a livello cosmologico, sul destino dell’Universo, eppure rimane sconosciuta, per ora, alle nostre osservazioni. Analizzare la storia di questa ricerca significa, in parte, percorrere gli ultimi passi dell’umanità verso il cuore del mondo. Nel’900 si fa avanti la concezione che ciò che esiste non è semplicemente quello che vediamo. In arte, letteratura, filosofia la mente comincia ad andare oltre ciò che appare. La ricerca della materia oscura in campo astronomico rappresenta il culmine scientifico di queste concezioni sulla realtà. La seguente tesina tratterà delle prove che gli astronomi posseggono sull’esistenza della materia oscura nei gradi spazi cosmici. La trattazione avrà un’impostazione soprattutto di tipo qualitativo, essendo l’analisi quantitativa di questi problemi molto complessa per essere trattata a livello liceale. La sola descrizione delle scoperte basterà a dare un quadro complessivo su ciò che oggi sappiamo sulla presenza di materia oscura nel cosmo, lasciando, ovviamente, molti interrogativi per il futuro. Mi propongo di approfondire le prove a sostegno della presenza di materia oscura, analizzando prima strutture più piccole come le galassie (parte 1) , per poi passare a strutture a larga scala come ammassi e superammassi (parte 2). Seguirà una piccola trattazione di carattere cosmologico (parte 3) e degli accenni sulle particelle elementari che potrebbero comporre la materia oscura (parte 4). A contorno di questo nucleo centrale ho posto due parti in ordine cronologico. La tesina infatti si apre con le prime evidenze sulla materia oscura del 1933, e si chiude con le ultimissime scoperte del gennaio 2007
Materie interessate: Fisica, Scienze, Matematica
Scarica la tesina:
https://www.matematicamente.it//tesine/Davide_Gerosa-Do_I_dare_disturb_the_universe.part01.pdf https://www.matematicamente.it//tesine/Davide_Gerosa-Do_I_dare_disturb_the_universe.part02.pdf
Tesina vincitrice del concorso "Premio Maturità 2007": prima tesina in assoluto
Commenti della giuria e degli esperti consultati
………………………………………………………………………
Quello della materia oscura è un tipico esempio di problema interdisciplinare, la cui trattazione presenta la difficoltà di richiedere competenze in settori scientifici molto diversi tra loro, nonché una grande capacità di sintesi nell’atto di tradurre le proprie conoscenze in risultati scientifici innovativi. A nostro parere, il lavoro di Davide Gerosa copre in modo esauriente i diversi aspetti del problema, giungendo ad un alto livello di approfondimento nell’aspetto cosmologico relativo alle evidenze osservative della presenza della materia oscura nell’Universo, ed impostando in modo corretto la complessa problematica dell’interpretazione circa la sua natura e costituzione. Il materiale presentato attesta il raggiungimento di conoscenze sufficienti ad intraprendere un più approfondito percorso investigativo circa l’attuale scenario sperimentale per la detezione di segnali prodotti da sorgenti di materia oscura con l.utilizzo delle più innovative tecnologie. Una nota molto positiva va espressa circa la grande originalità dell’elaborato, sia relativamente all’organizzazione e alla strutturazione del materiale proposto, sia riguardo alla ricchissima galleria fotografica ed ai molteplici riferimenti artistici di cui la tesina è costellata.
Erica Bisesi, PhD
………………………………………………………………………
Tesina strutturata in modo impeccabile, molto ampia che denota un lavoro attento e molto meticoloso. Talvolta molto tecnici e di alto livello i riferimenti che denotano una notevole padronanza delle difficili problematiche descritte. Si tratta di un lavoro eccellente sotto ogni punto di vista.
La giuria
Parole chiave: tesina di maturità, esame di stato liceo scientifico, astronomia, materia oscura.
Approfondimenti
 La Blogsfera è il mondo dei blog, una terra vastissima che oggi occupa una discreta fetta del Web. Un blog è una specie di contenitore, in cui il blogger ripone tutto ciò che vuole comunicare agli altri. E’ facile fare un’analogia tra il blog e il diario. Ci sono delle differenze però: il diario è segreto, quasi per antonomasia; il blog è pubblico, quasi per definizione. Ci sono blog su tutti gli argomenti dello scibile umano: la pesca, il formaggio, il tennis e la matematica. Certo, il mondo e’ bello perché è vario.
La Blogsfera è il mondo dei blog, una terra vastissima che oggi occupa una discreta fetta del Web. Un blog è una specie di contenitore, in cui il blogger ripone tutto ciò che vuole comunicare agli altri. E’ facile fare un’analogia tra il blog e il diario. Ci sono delle differenze però: il diario è segreto, quasi per antonomasia; il blog è pubblico, quasi per definizione. Ci sono blog su tutti gli argomenti dello scibile umano: la pesca, il formaggio, il tennis e la matematica. Certo, il mondo e’ bello perché è vario.
 Anna Cerasoli presenta il suo secondo racconto di Metallica, una piccola ‘femme fatale’ per il povero protagonista, che in fondo preferirebbe darle un bacio, invece di studiare calcolo combinatorio con lei: quante parole ci vogliono per un timido! Il primo numero era dedicato al problema ‘cosa mi metto’. In questo episodio Metallica e il suo amico devono affrontare il ‘Modello quante parole’.
Anna Cerasoli presenta il suo secondo racconto di Metallica, una piccola ‘femme fatale’ per il povero protagonista, che in fondo preferirebbe darle un bacio, invece di studiare calcolo combinatorio con lei: quante parole ci vogliono per un timido! Il primo numero era dedicato al problema ‘cosa mi metto’. In questo episodio Metallica e il suo amico devono affrontare il ‘Modello quante parole’.
 Dopo aver riproposto la definizione di Coxeter di poligono stellato si mostra come, utilizzando questo concetto, si possano dimostrare “geometricamente” alcuni teoremi importanti della Teoria dei Numeri.
Dopo aver riproposto la definizione di Coxeter di poligono stellato si mostra come, utilizzando questo concetto, si possano dimostrare “geometricamente” alcuni teoremi importanti della Teoria dei Numeri.
 Wikipedia è una enciclopedia presente in rete in 250 lingue, che si distingue dalle enciclopedie tradizionali essenzialmente per due motivi: il suo contenuto è liberamente consultabile, riproducibile e riutilizzabile, perché rilasciato con una licenza libera; chiunque può partecipare alla scrittura delle pagine.
Wikipedia è una enciclopedia presente in rete in 250 lingue, che si distingue dalle enciclopedie tradizionali essenzialmente per due motivi: il suo contenuto è liberamente consultabile, riproducibile e riutilizzabile, perché rilasciato con una licenza libera; chiunque può partecipare alla scrittura delle pagine.
Tesina per la maturità, scuola navale militare
Questa è la tesina sui frattali che ha vinto il premio per la migliore tesina in ambito scientifico.
In questa tesina si parla di frattali, un argomento relativamente nuovo che sta affascinando molti studiosi e incuriosendo anche il pubblico meno esperto; dopo una breve premessa sulle geometrie non euclidee che sono alla base della geometria frattale si addentra nell’analisi delle caratteristiche di queste curiose figure. Alle analisi, accompagnate da esempi e dimostrazioni, segue una descrizione dei frattali e dei metodi di costruzione frattale più importanti e un’introduzione alla teoria del caos sia dal punto di vista fisico, attraverso gli attrattori e l’entropia, che da un punto di vista filosofico esplorando le possibili conseguenze nel pensiero umano. Dopo una breve ma significativa galleria sulla nuova arte frattale, la tesina si conclude con la motivazione del suo titolo. Per quanto concerne la bibliografia e la sitografia sono stati segnalati tutti i testi e i siti consultati, anche se utilizzati solo per semplici spunti nello sviluppo dei molti argomenti trattati.
Indice
• Introduzione pag. 2
• Premessa pag. 2
• La geometria di Reimann pag. 3
• Cos’è un frattale? pag. 4
• Autosimilarità pag. 5
• Perimetro illimitato pag. 6
• Perimetro nullo pag. 7
• L’insieme di Cantor pag. 7
• Area finita pag. 9
• Dimostrazione col fiocco di neve di Von Koch pag. 9
• Area nulla pag. 12
• Il triangolo di Sierpinski pag. 12
• Dimensione non intera pag. 14
• Struttura complessa a tutte le scale di riproduzione pag. 16
• Dinamica caotica pag. 17
• Il problema delle tangenti alle curve frattali pag. 19
• Il metodo IFS sviluppato da Michael E. Barnsley pag. 20
• Un esempio: la costruzione della felce pag. 21
• Frattali creati con la tecnica L-System pag. 22
• L’insieme di Benoit Mandelbrot pag. 24
• Benoit Mandelbrot (biografia in lingua inglese) pag. 27
• Benoit Mandelbrot (biografia in lingua italiana) pag. 29
• Gli insiemi di Gaston Julia pag. 30
• Come costruire un frattale pag. 33
• Metodo dell’autosomiglianza pag. 33
• Metodo del gioco del caos pag. 34
• Metodo del triangolo di Tartaglia pag. 35
• Entropia ed attrattori pag. 36
• I frattali e l’Universo pag. 37
• La teoria del caos pag. 42
• Arte frattale pag. 47
• Eadem mutata resurgo pag. 49
• Bibliografia pag. 50
• Sitografia pag. 51
• Ringraziamenti pag. 52
Scarica la tesina sui frattali completa
Tesina vincitrice "Premio maturità 2007": miglior tesina in Ambito Scientifico
Commento della giuria
Lavoro molto lungo e laborioso. Spesso il candidato tratta argomenti molto tecnici e difficili, come il concetto di dimensione di un insieme frattale. Si trovano errori matematici anche nella parte introduttiva, poco chiara la connessione tra frattale e geometria non euclidea, gli errori tuttavia sono trascurabili rispetto alla complessità dell’argomento e tollerabili quando si cerca di spiegare la matematica a parole. Complessivamente il lavoro e’ eccellente.
 Matematico, regista, critico d’arte, dal 1997 organizza a Venezia il convegno internazionale ”Matematica e cultura” che ha lo scopo di approfondire le connessioni tra matematica e altri aspetti del sapere. Ha vinto il premio Galileo nel 1998 ed ha realizzato 18 film sul tema matematica e arte. Ultima sua creatura il libro ”Visibili armonie” (ed. Boringhieri, 2006) un racconto molto personale alla ricerca di alcuni ”fili d’Arianna” per cercare di rendere visibile il legame tra matematica, arte e cultura. Un viaggio alla ricerca di segni e numeri lasciati da artisti e scienziati durante il quale lei afferma che ”la matematica apre nuove strade alla creatività”.
Matematico, regista, critico d’arte, dal 1997 organizza a Venezia il convegno internazionale ”Matematica e cultura” che ha lo scopo di approfondire le connessioni tra matematica e altri aspetti del sapere. Ha vinto il premio Galileo nel 1998 ed ha realizzato 18 film sul tema matematica e arte. Ultima sua creatura il libro ”Visibili armonie” (ed. Boringhieri, 2006) un racconto molto personale alla ricerca di alcuni ”fili d’Arianna” per cercare di rendere visibile il legame tra matematica, arte e cultura. Un viaggio alla ricerca di segni e numeri lasciati da artisti e scienziati durante il quale lei afferma che ”la matematica apre nuove strade alla creatività”.
 Se osservassimo il cielo stellato durante tutta la nostra esistenza difficilmente noteremmo sostanziali modifiche. Al più può capitare che qualche cometa di passaggio decida di farci visita o che una stella nova faccia la sua apparizione in cielo. La forma delle costellazioni così come la conosciamo resterebbe però sostanzialmente immutata. Le stelle sembrano indifferenti al tempo che scorre, come destinate ad una sorta di vita eterna. In realtà si tratta di una illusione dovuta all’estrema brevità della vita media di un essere umano se confrontata con quella tipica delle stelle.
Se osservassimo il cielo stellato durante tutta la nostra esistenza difficilmente noteremmo sostanziali modifiche. Al più può capitare che qualche cometa di passaggio decida di farci visita o che una stella nova faccia la sua apparizione in cielo. La forma delle costellazioni così come la conosciamo resterebbe però sostanzialmente immutata. Le stelle sembrano indifferenti al tempo che scorre, come destinate ad una sorta di vita eterna. In realtà si tratta di una illusione dovuta all’estrema brevità della vita media di un essere umano se confrontata con quella tipica delle stelle.
La soluzione del crucinumero del n° 2

|
|
|
Marcus du Sautoy, L’enigma dei numeri primi , Rizzoli, 2005
“Quello che Riemann aveva fatto era stato prendere ciascuno dei punti situati a livello del mare sulla mappa del mondo immaginario. Da ciascun punto aveva creato un’onda, una nota emessa da un qualche strumento matematico. Combinando tutte queste onde, ottenne un’orchestra che suonava la musica dei numeri primi. La coordinata nord-sud di ogni punto a livello del mare controllava la frequenza dell’onda, ovvero l’altezza della nota corrispondente. Al contrario, la coordinata est-ovest controllava, come aveva compreso Eulero, l’intensità alla quale ciascuna nota sarebbe stata suonata. Tanto maggiore era l’intensità della nota, quanto più grandi erano le fluttuazioni del suo grafico ondulato. A Riemann interessava capire se qualcuno degli zeri suonasse con un’intensità significativamente maggiore rispetto agli altri. Un tale zero avrebbe prodotto un’onda il cui grafico avrebbe oscillato più delle altre onde e quindi avrebbe avuto un ruolo maggiore nel conteggio dei numeri primi. Dopo tutto, sono le altezze di queste onde che controllano la differenza fra la stima di Gauss e il vero numero di numeri primi ”. Il problema era dunque conoscere la distribuzione degli zeri della funzione zeta e vedere quanto a est nel paesaggio zeta si presentassero. Per vederci più chiaro, Riemann decise di calcolare alcuni dei punti a ‘livello del mare’ per vedere con precisione dove si trovassero. “Quando cominciò ad analizzare l’esatta collocazione di questi punti, ebbe una grossa sorpresa. Invece di essere sparpagliati qua e là su tutta la mappa, di modo che alcune note sarebbero risultate più intense di altre, gli zeri che calcolava sembravano disporsi come per miracolo su una linea retta che attraversa il paesaggio nella direzione nord-sud. Era come se ogni punto situato a livello del mare avesse la stessa coordinata est-ovest, uguale a ½”.
|
 Il confine tra matematica e filosofia non è sempre ben netto e definito; a volte le due discipline tendono a fondersi, soprattutto quando gli oggetti di studio sono temi riguardanti l’essenza di ciò che non è tangibile dall’uomo, cose la cui natura non può essere appurata osservando con gli occhi o toccando con mano, ma che possono essere solo percepite, spesso neanche appieno, dalla mente umana. Non è un caso che molti grandi pensatori della storia siano ricordati come pietre miliari ed esempi da seguire sia dai matematici che dai filosofi. Tutto ciò non deve stupire, dato che entrambe le discipline sono naturali evoluzioni del pensiero umano, sono manifestazioni della volontà dell’uomo di capire ciò che accade attorno a sé. Più ci si spinge oltre e più questa comprensione risulta difficile, poiché diminuiscono le capacità umane di verificare l’ortodossia delle proprie idee; addirittura, la possibilità di trovare risposte certe viene meno quando si cerca di comprendere la natura di ciò che non è contabile o misurabile, non ha inizio né fine, insomma è infinito… come i numeri… come Dio!
Il confine tra matematica e filosofia non è sempre ben netto e definito; a volte le due discipline tendono a fondersi, soprattutto quando gli oggetti di studio sono temi riguardanti l’essenza di ciò che non è tangibile dall’uomo, cose la cui natura non può essere appurata osservando con gli occhi o toccando con mano, ma che possono essere solo percepite, spesso neanche appieno, dalla mente umana. Non è un caso che molti grandi pensatori della storia siano ricordati come pietre miliari ed esempi da seguire sia dai matematici che dai filosofi. Tutto ciò non deve stupire, dato che entrambe le discipline sono naturali evoluzioni del pensiero umano, sono manifestazioni della volontà dell’uomo di capire ciò che accade attorno a sé. Più ci si spinge oltre e più questa comprensione risulta difficile, poiché diminuiscono le capacità umane di verificare l’ortodossia delle proprie idee; addirittura, la possibilità di trovare risposte certe viene meno quando si cerca di comprendere la natura di ciò che non è contabile o misurabile, non ha inizio né fine, insomma è infinito… come i numeri… come Dio!
Ecco perché la ricerca dell’Infinito in tutte le sue forme è stata terreno di battaglie sia per matematici che teologi, dai grandi pensatori greci ai mistici ebraici, dai filosofi del Seicento alla florida generazione matematica ottocentesca. “Il mistero dell’alef” è un’accurata ricostruzione storica di questa ricerca, che ha affascinato, ma al contempo turbato, chiunque si sia avvicinato ad essa; ha fatto intravedere la luce a qualcuno e ha fatto impazzire altri, ma soprattutto ha dimostrato che, nonostante le grandi energie profuse, quando cerca di toccare l’Infinito, l’uomo cade immancabilmente vittima di paradossi e contraddizioni, quasi come se all’essere umano fosse proibito cercare di capire qualcosa che è al di fuori della sua stessa natura finita. Stando a quanto ci racconta il libro, il primo incontro degli uomini con l’Infinito è stata la scoperta da parte dei Pitagorici dei numeri irrazionali, numeri con espansione decimale infinita non periodica; l’avvenimento turbò la comunità e causò perfino la morte di uno dei suoi membri. Anche gli Ebrei si interessarono all’Infinito, a partire dal periodo immediatamente successivo alla Diaspora: essi elaborarono una filosofia basata sulla meditazione e sulla contemplazione di Dio che aveva come fine ultimo la percezione dell’En Sof, ovvero l’Infinità di Dio. Un impulso fortissimo lo diedero Galileo Galilei e Bernhard Bolzano, i quali prepararono la strada all’uomo che meglio di ogni altro simboleggia la ricerca dell’Infinito: Georg Cantor. Gran parte del libro è dedicata alla vita e al lavoro di questo grande matematico, che, avvalendosi dei potenti strumenti della sua nuova creazione, la teoria degli insiemi, ha ipotizzato una struttura armonica e ordinata nel caos e nel mistero che avvolge il concetto di Infinito. Cantor dimostrò, con una tecnica ingegnosa nota come “argomento diagonale”, che l’insieme dei numeri razionali è numerabile, ovvero ha la stessa cardinalità dell’insieme dei numeri naturali: sembra paradossale, anche Cantor stentava a crederci nonostante lo avesse dimostrato, ma i numeri razionali sono esattamente tanti quanti i numeri naturali. Dimostrò inoltre che i numeri reali non sono numerabili, ma sono infinitamente più numerosi dei razionali; ecco come il generico concetto di Infinito veniva esteso a vari livelli. Ma esistono solo questi due tipi di Infinito? Cantor ipotizzò l’esistenza di un numero più grande di ogni altro numero finito e lo indicò con la lettera greca $omega$. Poi ipotizzò l’esistenza di altri numeri di questo tipo, dunque numeri “infiniti”, a cui diede il nome di numeri transfiniti; teorizzò anche un’aritmetica per effettuare operazioni con questo genere di numeri. Per Cantor i numeri transfiniti sono a loro volta in quantità infinita e in seguito utilizzò la lettera ebraica $aleph$ (si pronuncia alef) per indicare ogni elemento della loro successione. Ecco dunque il susseguirsi infinito di questi numeri così grandi da superare qualunque quantità finita che la mente umana possa immaginare: $aleph_0, aleph_1, aleph_2, aleph_3, ldots$. La grandiosità dell’idea di Cantor non risiede, però, solo nell’aver ipotizzato l’esistenza di questi numeri. Cantor andò oltre: riteneva che $aleph_0$, il più piccolo dei numeri transfiniti, fosse pari alla cardinalità dell’insieme dei numeri naturali (quindi anche a quella dei razionali); sosteneva inoltre che la potenza dell’insieme dei numeri reali fosse $aleph_1$… in sostanza, per Cantor, i tipi di Infinito con cui aveva a che fare maggiormente l’uomo non erano altro che i due tipi più “piccoli” di Infinito! Come è noto, l’insieme dei reali costituisce un insieme continuo (contrapposto a quello dei razionali che è un insieme discreto). Ciò premesso, Cantor congetturò che il nesso tra i due tipi di Infinito più noti fosse tutt’altro che complesso: $2^{aleph_0} = aleph_1$. Questa equazione è tuttora nota come “l’ipotesi del continuo”; colui che la formulò tentò con tutti i propri mezzi di dimostrarla, ma non vi riuscì. In seguito, numerosi matematici, Gödel su tutti, hanno continuato a costruire sulle basi gettate da Cantor. Grazie al lavoro di Gödel e di Cohen fu dimostrato che l’ipotesi del continuo non può essere dimostrata all’interno del nostro sistema matematico, dunque non possiamo sapere se l’idea di Cantor fosse giusta o meno. La malattia mentale che tormentò Cantor, Gödel e altri che come loro si sono addentrati molto in profondità lungo quella via potrebbe essere intesa come un monito divino a non sfidare entità più grandi di noi; di contro, potrebbe essere un effetto dell’estasi di aver visto uno spiraglio di luce proveniente da un mondo le cui porte nessuno ha mai varcato. Probabilmente all’uomo non è dato di conoscere l’Infinito, ma solo a pochi eletti è concesso di percepirlo, di avvertirlo, di intravederlo. Forse, come ha sempre sostenuto lo stesso Cantor, l’Infinito nella sua essenza (egli soleva definirlo l’Assoluto) è Dio stesso, ecco spiegato perché per il genere umano è del tutto impossibile una comprensione dell’Infinito nella sua pienezza. Forse è così, ma anche questo probabilmente non ci è dato poter sapere. Come dicevano gli antichi, dunque, scire nefas? Soltanto Dio lo sa…
 Un’equazione matematica è la massima sintesi di un lungo lavoro di ricerca e di un faticoso avvicinamento alla conoscenza del mondo ma anche il punto di partenza per il dominio dell’uomo sulla natura.
Un’equazione matematica è la massima sintesi di un lungo lavoro di ricerca e di un faticoso avvicinamento alla conoscenza del mondo ma anche il punto di partenza per il dominio dell’uomo sulla natura.
Per arrivare alla formula definitiva, il percorso è tutt’altro che facile.
Lo scienziato, almeno secondo il punto di vista dell’autore di questo libro, deve avere forti motivazioni psicologiche, che lo spingono, sin dall’infanzia, a una ricerca continua della soluzione di un problema. Quando il problema sarà risolto e l’equazione sarà scritta definitivamente l’intera umanità ne resterà sconvolta.
Nel linguaggio della matematica, le equazioni sono come la poesia: dimostrano dati reali con ineguagliabile precisione, trasmettono quantità di informazioni in tempi relativamente brevi; e spesso la loro comprensione è inaccessibile ai profani. E come la poesia tradizionale ci aiuta a sondare in profondità dentro noi stessi, allo stesso modo la poesia matematica ci aiuta a vedere molto al di là di noi stessi: se non proprio a capire i misteri dell’invisibile, per lo meno a raggiungere i margini dell’universo visibile.
L’autore si propone di spiegarci, senza usare altre formule matematiche, il significato e la storia di cinque delle equazioni che hanno cambiato il nostro mostro modo di vivere e di concepire il mondo. Il libro si compone di cinque storie, ognuna delle quali dedicata a un’equazione. La struttura narrativa è simile per tutti e cinque le storie.
Ogni racconto è suddiviso in cinque capitoli. Nel prologo viene raccontato qualche episodio drammatico circa la vita del personaggio principale, episodio che sarà il motivo di fondo della storia e porterà il personaggio alla costruzione dell’equazione. Il capitolo "Veni " racconta il modo in cui lo scienziato viene a contatto con il problema scientifico. "Vidi " è il capitolo dedicato alla descrizione della complessità storica del problema. "Vici " è il racconto di come lo scienziato ha vinto il problema. Nell’Epilogo viene mostrato il modo in cui l’equazione ha segnato, anche dal punto di vista tecnologico, il nostro modo di vivere.
Ma vediamo come l’autore ha raccontato queste storie.
La prima equazione è la legge di gravitazione universale di Newton. Il tredicenne Isaac Newton è uno dei peggiori studenti della scuola superiore, deriso dai suoi compagni ed emarginato dalla classe. Il bulletto di turno, un certo Storer, lo prende a calci ma improvvisamente Isaac trova la forza di rispondere alle provocazioni e dopo tre pagine di rissa finalmente ne viene fuori vincitore. L’autore conclude: Nei decenni che seguirono, l’interesse di Newton si sarebbe spostato dai mulini a vento all’universo in generale. Ma una cosa in lui non sarebbe cambiata: avrebbe incontrato altri antagonisti – o supposti tali – e ogni volta il suo ossessivo desiderio di rivalsa e di approvazione lo avrebbe spinto a una comprensione del mondo naturale senza precedenti. … L’emozione procurataci dalla stupefacente scoperta di Newton ci avrebbe sopraffatti e alla fine le belle idee nutrite su Dio e sul paradiso sarebbero crollate proprio come quel gradasso di Storer.
Non è ben chiaro se l’autore abbia raccontato un fatto documentato o un fatto che accade a tutti i ragazzi di tredici anni. In ogni caso, il passaggio da una rissa tra ragazzini alla scoperta di una legge universale mi sembra piuttosto ardita.
Il libro di Guillen si presenta sin dalle prime pagine non come una storia delle equazioni ma come un romanzo sulla vita di alcuni scienziati. Un romanzo che è sicuramente avvincente, come dimostra la fortuna che ha avuto, ma che delude chi desidera capire i fatti storici e l’evoluzione delle teorie scientifiche. Le cinque pagine del prologo di questa storia sono infatti un racconto libero sull’infanzia di Newton e appena due righe sono dedicate al quadro scientifico-filosofico di riferimento: l’universo è suddiviso in due regni, ognuno dei quali obbedisce a una diversa serie di leggi scientifiche e queste leggi erano state sancite in modo definitivo da Aristotele duemila anni prima di Newton. Nel capitolo Veni si racconta della nascita di Newton, delle alterne fortune della madre, della salute cagionevole del piccolo Isaac, dei continui allontanamenti e ricongiungimenti dalla madre, della sua iscrizione al Trinity College, del fatto che la madre, nonostante fosse abbastanza ricca gli negasse il mantenimento agli studi, fino al famoso episodio della mela, descritto con toni mistici: Un giorno, il tempo era così bello e Newton così immerso nei suoi pensieri, che egli non si accorse che si stava facendo tardi. A poco a poco il giardino tutt’intorno cominciò a rosseggiare, inondato dalla soffice luce dorata che è prerogativa dei tramonti estivi. Improvvisamente il tonfo provocato da una mela caduta da un albero vicino fece sussultare il giovane, distogliendolo dalle sue profonde meditazioni. Nei pochi attimi che gli occorsero per tornare in sé, sull’orizzonte orientale apparve lentamente il bordo superiore di un’enorme Luna piena. L’aneddoto sulla mela l’abbiamo imparato tutti nei primi anni di scuola, Guillen non ci dice niente di scientificamente apprezzabile se non il desiderio di Newton di voler cercare una connessione tra i due fatti: la caduta della mela e la rotazione della Luna intorno alla Terra. Ma poiché "occorreranno vent’anni affinché Newton perfezionasse e rendesse pubblici i suoi risultati" il lettore aspetta paziente di leggere nelle ultime pagine del racconto cosa farà Newton nei venti anni che seguono questo famoso episodio. Sullo sfondo del racconto dei primi anni di vita di Newton viene abbozzata a grandi linee la storia dell’Inghilterra di quegli anni, con le guerre civili e religiose.
Guillen ci propone un ardito passaggio: Per buona parte del XVII secolo il mondo, nell’ambito politico come in quello scientifico, venne diviso in due regni nettamente separati. I comuni mortali abitavano il regno terrestre, e al di sopra di esso c’erano solo i sovrani; questi ultimi risiedevano in una specie di territorio elevato e celestiale, dispensati dal dovere di osservare il complesso di severe leggi e norme che loro stessi imponevano ai sudditi, e ai parlamenti. L’autore intende formulare una analogia che si potrebbe sintetizzare in una proporzione matematica: i sovrani stanno ai sudditi come la Luna sta alla mela. Di conseguenza, la ‘scoperta’ di Newton non sarà una semplice ‘rivoluzione’ scientifica ma anche una ‘rivoluzione’ politica: se le leggi che governano il mondo celeste, nel quale risiede la Luna, sono le stesse del mondo terrestre nel quale cadono le mele allora anche i sovrani e i sudditi devono sottostare alle stesse leggi.
Dopo numerose pagine di biografia, l’equazione della legge gravitazionale spunta fuori quasi improvvisamente preannunciata dalla solita passeggiata serale al sorgere della Luna. Interessante è invece il capitolo Vidi, nel quale viene descritta una breve ma chiara storia della cosmologia da Platone a Galileo.
La seconda equazione è la legge della pressione idrodinamica di Daniel Bernoulli. Anche qui, la storia dell’equazione è in realtà una biografia di Daniel Bernoulli e della sua famiglia di rissosi matematici. Il capitolo sugli antefatti scientifici di questa legge è piuttosto scarno e poco coerente. La scoperta di Daniel Bernoulli diviene una semplice modifica della legge di Leibniz sulla forza viva (energia cinetica) , la prima è la formula di Leibniz, la seconda quella di Bernoulli. Il significato dell’equazione di Bernoulli viene spiegato con un’analogia piuttosto discutibile: Potremo rappresentare la scoperta di Bernoulli come il tentativo di un lobbista di influenzare il voto del senato si qualche questione politica. Quanto più velocemente egli si dà da fare in giro – cioè suddivide il proprio tempo – tanto meno riesce a far pressione su ciascun politico.
La terza equazione è la legge dell’induzione elettromagnetica di Faraday. Il racconto di questa equazione è quasi tutto dedicata alla biografia di Michael Faraday. Ma l’equazione, come è stato giustamente messo in evidenza nel libro, non è opera di Faraday, scienziato autodidatta, poco propenso alla matematica e interessato esclusivamente all’aspetto sperimentale dell’elettromagnetismo. Faraday è autore degli esprimenti che hanno messo in luce lo stretto rapporto tra elettricità e magnetismo ed ha formulato la legge dell’induzione elettromagnetica in termini descrittivi. L’autore dell’equazione è invece J. C. Maxwell che in questa storia sulle equazioni che hanno cambiato il mondo occupa un posto marginale.
E’ strano che Guillen abbia preferito, in una storia sulle equazioni, trattare la figura di uno scienziato sperimentale come Faraday invece di un teorico come Maxwell, vero autore delle equazioni sull’elettromagnetismo.
La quarta equazione è il secondo principio della termodinamica di Clausius. Guillen sposta il piano del racconto dalla decadenza, e quindi dalla morte, di un sistema chiuso, come può essere l’universo, alla vita e le vicende personali di Rudolf Clausius; dai fatti scientifici e le loro implicazioni il lettore viene condotto a meditare sulla ‘morale’ che se ne può ricavare da un’equazione e dalla vita di un uomo. Nel racconto, Clausius si chiede continuamente "Ma, se solo avesse potuto, avrebbe rimesso l’orologio ancor più indietro, riportando il tempo a prima di …" E’ il modo scelto da Guillen di introdurre il tema dei fenomeni irreversibili.
Un’osservazione a margine: è evidente che si tratta di una disequazione e non di una equazione, l’autore non lo precisa nemmeno all’interno del testo: "… lo stupefacente risultato raggiunto si condensava nella seguente equazione: ". Forse è un cercare il pelo nell’uovo oppure l’autore ha perso l’occasione per spiegare la differenza tra l’equazione che stabilisce un legame di corrispondenza tra masse, distanze e forze (è il caso dell’equazione di Newton, per la quale disponendo due ben precise masse a una ben precisa distanza si può ricavare esattamente la forza che le lega le due masse) e una disequazione che stabilisce che una quantità è maggiore di un’altra ma non ci dice di quanto è maggiore.
La quinta equazione $E=Mc^2$ è detta ‘relatività ristretta’ di Einstein. Il lettore avrebbe meritato un chiarimento circa il fatto che le equazioni della relatività ristretta, quelle che regolano i cambiamenti da un sistema di riferimento a un altro, si chiamano trasformazioni di Lorentz, o al più Lorentz-Poincaré, e che il contributo di Einstein alla relatività ristretta è stato piuttosto marginale. Il racconto di Guillen sull’equazione "che ha spento la luce" è come al solito una racconto sulla vita di Einstein a partire dalla primavera del 1895, quando durante una passeggiata sulle Alpi il futuro scienziato ha rischiato di morire. Il sedicenne Einstein, trovandosi "d’improvviso faccia a faccia con la morte" ne deve aver ricavato una qualche filosofia di vita che Guillen fa fatica a descrivere. Più avanti Guillen ci regala una delle solite banalità e luoghi comuni: "il bambino fu tardo nel parlare, nel leggere, nell’apprendere. In breve, sembrava tutt’altro che destinato a grandi imprese." Più avanti avanti ancora il lettore si imbatte in una grande confusione su un misterioso fattore di contrazione: Il fattore di contrazione, graficamente (sic!, forse "simbolicamente"? ) rappresentato con 1-s, si riferisce a ogni processo in cui l’insieme di un fenomeno – un conto bancario, un serbatoio di gas, la reputazione, qualsiasi cosa – veniva contratto, ridotto di una piccola quantità s. Ad esempio, 1-0,01 significava che, diciamo, il contenuto di una boccetta di profumo era stato ridotto di un centesimo della sua quantità originale: insomma, di un leggere spruzzo. … Per qualsiasi matematico in erba, questa formula rappresentava un indispensabile trucco del mestiere. Per Einstein era il bastone da montagna che lo avrebbe aiutato nei saliscendi lungo un insidioso crinale delle sue idee rivoluzionarie sulla natura. L’episodio di Einstein mi sembra quello meno riuscito del libro ma soprattutto mi sembra dannoso far credere che uno ‘spruzzo’ di 1-s sia un trucco di mestiere per un matematico e un potente strumento per capire la relatività. Antonio Bernardo
|
Tanti di noi consoceranno la storiella dello scimpanzé rinchiuso in uno stanzino d’osservazione. Appesa fuori dalla sua portata c’è una banana. Un ricercatore volendo testare l’abilità mentale dell’animale entrò nello stanzino per disporre qua e là alcuni cassettoni, supponendo che lo scimpanzé ne avrebbe fatto una catasta per raggiungere la banana. La scimmia osservò tranquilla il ricercatore e nel momento in cui egli passò proprio sotto la banana fece uno scatto e, saltandogli sulla schiena, agguantò al volo l’ambito frutto. La morale di questa storia è: problemi reali non hanno mai solo soluzioni previste in anticipo e il contesto di un problema è importante quanto il problema stesso. pag. 18 |
Antonio Bernardo |
I nostri giochi di matemagica
Associare a ogni grafico a torta la frazione che ne rappresenta la parte di colore giallo.
|
|
 Il gioco consiste nello spostare il cavallo su una scacchiera secondo la regola del gioco degli scacchi, con un movimento a L, in modo da toccare tutte le caselle della scacchiera nel minor numero di mosse possibili. E’ possibile ritornare sulle caselle già toccate ma non è consigliabile, perché la soluzione minima si ottiene con 63 mosse, cioè senza mai ripassare due volte per la stessa casella. Ci vuole una strategia vincente! Un gioco non semplice. Da un punto di vista strettamente matematico il problema si risolve con grafi Euleriani ed Hamiltoniani. Le soluzioni possibili sono 122.802.512, non dovrebbe essere difficile trovarne qualcuna.
Il gioco consiste nello spostare il cavallo su una scacchiera secondo la regola del gioco degli scacchi, con un movimento a L, in modo da toccare tutte le caselle della scacchiera nel minor numero di mosse possibili. E’ possibile ritornare sulle caselle già toccate ma non è consigliabile, perché la soluzione minima si ottiene con 63 mosse, cioè senza mai ripassare due volte per la stessa casella. Ci vuole una strategia vincente! Un gioco non semplice. Da un punto di vista strettamente matematico il problema si risolve con grafi Euleriani ed Hamiltoniani. Le soluzioni possibili sono 122.802.512, non dovrebbe essere difficile trovarne qualcuna.
|
Il punto P in coordinate polari P(r,ß) Lemniscata Pera Cardioide Spirale di Archimede Cicloide La cicloide estesa presenta un paradosso: mentre la ruota avanza alcuni suoi punti tornano indietro in prossimità del cappio centrale.
|
.
L’autore si propone di percorrere la storia del pensiero matematico attraverso brevi descrizioni delle curve piane, che per vari motivi sono divenute famose. Per ciascuna curva è riportata la notazione matematica che permette di rappresentarla: a volte l’equazione cartesiana, altre le equazioni parametriche, altre ancora l’equazione polare. L’ equazione cartesiana è quella che lega l’ ascissa x con l’ ordinata y riferite ad un sistema di assi cartesiani . Per esempio, x2 +y2 =1 rappresenta un cerchio, x2 -y2 =1 un’iperbole, x2 +2y2 =1 un’ellisse, y=x2 una parabola. Le equazioni parametriche sono invece due per ciascuna curva del piano; hanno questo nome perché l’ascissa x e la ordinata y si ottengono per mezzo di un parametro variabile t. Per esempio, la lemniscata , una curva a forma di otto, ha equazioni x=sint·cost, y=cost; la pera ha equazioni x=1+cost, y=1/(1+sint); la cardioide ha equazioni x=2cost-cos2t, y=2sint-sin2t. Il bicorno , o cappello a due punte, ha equazioni x=cost, y=sin2 t/(2+sint). L’ equazione polare di una curva è una relazione che lega la distanza r, di un generico punto P (della curva) dall’origine O ( polo ), con l’angolo ß, formato dalla retta OP con una semiretta fissata (asse polare ). Solitamente si usano le lettere greche RO e TETA; per esigenze di caratteri ho usato r e ß. Un esempio è costituito dalla spirale di Archimede: r=ß. Tra le curve di particolare interesse non poteva mancare un’analisi storica della cicloide o roulette. La curva, studiata per primo da Pascal, è il percorso che fa nell’aria il punto di una ruota, quando questa compie una rotazione completa. Le sue equazioni parametriche sono x=r(t-sint), y=r(1-cost). Può essere estesa se il punto è posto all’esterno della circonferenza, contratta se il punto è all’esterno delle circonferenza. Da ricordare il paradosso della cicloide estesa. Le ruote del treno, per esempio, hanno una flangia che fuoriesce dalla ruota vera e propria e serve per non far uscire la ruota dal binario. Mentre la ruota rotola sul binario un punto della flangia esterna descrive una cicloide con un piccolo cappio. Proprio mentre descrive questo cappio, il punto è costretto a tornare indietro. Da qui il paradosso: come è possibile che i punti della flangia tornino indietro mentre il treno avanza? Un’altra curva particolarmente interessante è la catenaria , studiata da Huygens. E’ la curva formata da una catena, o anche dal cavo della luce, sospesa ai suoi estremi. L’equazione cartesiana è y=(a/2)·cosh(x/a), ricordando la definizione di coseno iperbolico y= (a/2)(ex/a +e-x/a ). Infine la famosa curva a campana di Gauss particolarmente importante nelle distribuzioni statistiche. Nel libro non mancano i riferimenti alle curve del secolo scorso: la curva di Peano, la polvere di Cantor, la curva di Kock, i frattali di Mandelbrot. Un libro che incuriosisce, unendo notizie storiche, equazioni e disegni piacevoli.
Antonio Bernardo |
|
|
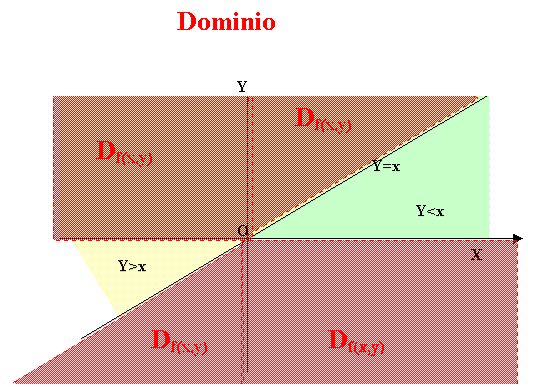
Assegnata la funzione $f(x,y) = frac{sqrt{y^2 – xy}}{2}$ determinare il dominio e le derivate parziali.
$f(x, y) = frac{1}{2} sqrt{y cdot (y – x)}$
Dominio: $y cdot (y – x) ge 0 Rightarrow {(y geq 0), (y – x geq 0):}$
Derivate parziali:
$f(x, y) = frac{1}{2}cdot sqrt{y^2-xy}$
$f_x = frac{1}{4} frac{-y}{sqrt{y^2 -xy}}$
$f_y = frac{1}{4} frac{2y – x}{sqrt{y^2-xy}}$
Si dimostri che tra tutti i cilindri inscritti in un cono circolare retto, ha volume massimo quello la cui altezza è la terza parte dell'altezza del cono.
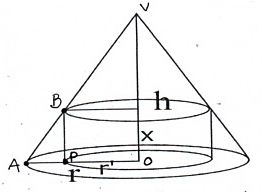
${(h = ext{altezza cono}), (r = ext{raggio cono}):}$
${(x = ext{altezza cilindro}),(r' = ext{raggio cilindro}),(0 < x <h):}$
$V = ext{volume cilindro}$
Dalla similitudine dei triangoli $APB$ e $AOV$ si ha
$r: h = (r- r') : x \\\\rightarrow r – r' = frac{r}{h} x \\\\rightarrow r' = r cdot (1 – frac{x}{h})$
$V = pi r^2 (1 – frac{x}{h})^2 cdot x = pi r^2 cdot (1 – frac{2x}{h} + frac{x^2}{h^2}) cdot x = pi cdot r^2 cdot (x – frac{2x^2}{h} + frac{x^3}{h^2})$
$V' = pi r^2 cdot (1 – frac{4}{h} x + frac{3}{h} x^2) = 0 \\rightarrow 3x^2 – 4hx + h = 0$
$x_{1,2} = frac{2h pm sqrt{4h^2 – 3h^2}}{3} = frac{2h pm h}{3} \rightarrow {(h ext{da scartare perché } x
e h),(frac{1}{3} h):}$
$x = frac{1}{3} h$ è punto di massimo per $V$, volume del cilindro.
Calcolare le seguenti derivate
$(\frac{a^2}{4a^2+4ab+b^2} – \frac{a-b}{6a+3b}):(\frac{a^3-b^3}{12a+6b])$
Soluzione
$\frac{a^2}{(2a+b)^2} – \frac{a-b}{3 (2a+b)}) : \frac{a^3-b^3}{6 (2a+b)}$
$\frac{3a^2-(a-b)(2a+b)}{3 (2a+b)^2}:\frac{a^3-b^3}{6 (2a+b)}$
$\frac{3a^2-(2a^2+ab-2ab-b^2)}{3 (2a+b)^2} \cdot \frac{6 (2a+b)}{a^3-b^3}$
$\frac{3a^2-2a^2-ab+2ab+b^2}{3 (2a+b)^2} \cdot \frac{6 (2a+b)}{a^3-b^3}$
$\frac{1}{(2a+b)} \cdot \frac{2}{(a-b)}$
$\frac{2}{(2a+b)(a-b)}$
$\frac{b+2}{b-2} – \frac{b+1}{b-1} – \frac{2}{b^2 – 3b +2}$
$\frac{b+2}{b-2} – \frac{b+1}{b-1} – \frac{2}{(b-1)(b-2)}$
$\frac{(b+2)(b-1)-(b+1)(b-2)-2}{(b-1)(b-2)}$
$\frac{b^2-b+2b-2-(b^2-2b+b-2)-2}{(b-1)(b-2)}$
$\frac{b^2-b+2b-2-b^2+2b-b+2-2}{(b-1)(b-2)}$
$\frac{2b-2}{(b-2)(b-1)}$
$\frac{2(b-1)}{(b-2)(b-1)}$
$\frac{2}{b-2}$
$[2a^4 – (a^2 + b + 1) (a^2 – b – 1)] [a^4 – (b + 1)^2] + (b + 1)^4$
I due fattori all'interno della prima coppia di parentesi quadre sono una differenza di quadrati.
$[2a^4 – (a^4 – (b + 1)^2] [a^4 – (b + 1)^2] + (b + 1)^4$
$[a^4 + (b + 1)^2] [a^4 – (b + 1)^2] + (b + 1)^4$
Le due parentesi quadre sono ancora una differenza di quadrati:
$a^8 – (b + 1)^4 + (b + 1)^4 = a^8$
$\frac{a – b}{a + b} – \frac{\ldots}{a^2 + 2ab + b^2} = \frac{a – 3b}{a+b}$
$\frac{(a – b) \cdot (a + b) – \ldots }{(a + b)^2} = \frac{a – 3b}{a + b}$
$\frac{(a-b)(a+b)-(a+b) \ldots}{(a+b)^2} = \frac{a – 3b}{a+b}$
$\frac{(a – b – \ldots )}{(a+b)} = \frac{a-3b}{(a+b)}
$a -b – ldots = a – 3b$
La quantità da cercare è quindi $2b (a+b)$.
Titolo completo: Progettazione degli impianti elettrici a servizio di uno stabilimento per la raccolta ed il trattamento in piattaforma di materie destinate al riciclo (CARTA, AL, CU, ELETTRONICA, LEGNO, VETRO).
Breve descrizione: Progettazione elettrica degli impianti dello stabilimento in oggetto.
Materie trattate: Impianti – Elettrotecnica – Tecnologia disegno e progettazione
Scarica la tesina:
https://www.matematicamente.it//tesine/Giuseppe_Gelsomino-Progettazione_degli_impianti_elettrici.pdf
.
|
Il libro è in parte il catalogo della mostra Matemilano , ideata e realizzata dal Dipartimento di Matematica dell'Università degli Studi di Milano con la collaborazione del Dipartimento di Matematica dell'Università di Trento, allestita per la prima volta nell'autunno 2003 presso il Museo Nazionale della Scienza e della Tecnologia "Leonardo da Vinci" di Milano. Se non potete andare a Milano potete accontentarvi di una visita virtuale http://matemilano.mat.unimi.it/presenta.htm Antonio Bernardo |
Analisi del sistema carcerario dagli studi classici a quelli moderni, al fine di comprendere se il carcere italiano sia ancora funzionale agli attuali bisogni della società.
Materie interessate: Filosofia, storia, scienze sociali, comunicazione, diritto, francese.
Scarica la tesina:
https://www.matematicamente.it//tesine/Fabrizio_Alberto-Il_carcere.zip
Un percorso sull'Etica che parte dalla distinzione tra questa e la Morale e arriva fino ai giorni nostri, toccando i punti salienti del suo sviluppo..
Materie trattate: Italiano, filosofia, fisica, storia, attualità, latino, inglese.
Scarica la tesina
https://www.matematicamente.it//tesine/Giulia_Manzi-L.utopia_dell.ethos.rar
La tesina si propone di ripercorrere le varie tappe del pensiero ateo, in accordo con la filosofia sartriana che ha come presupposto una posizione atea coerente..
Materie trattate: Greco,filosofia,latino,italiano,geografia astronomica.
Scarica la tesina
https://www.matematicamente.it//tesine/Rossella_Cavaliere-L.ateismo_A_un_umanismo_.zip
La tesina concerne una breve storia delle relazioni diplomatiche, con particolare attenzione all’atto della dichiarazione Balfour che portò alla nascita dello Stato di Israele, citando le strutture diplomatiche di ONU e NATO.
Materie trattate: storia – inglese
Analisi delle principali teorie cosmologiche dagli inizi del Novecento ad Oggi.
Materie interessate: Fisica, Geografia Astronomica, Letteratura Latina.
Scarica la tesina:
https://www.matematicamente.it/tesine/Antonio_Corsaro-Le_origini_dell_universo.rar
L’infinito non è solo un semplice concetto filosofico o matematico. Riguarda tutta la nostra vita, in ogni suo aspetto. Ed è questo che io ho cercato di dimostrare.
Materie interessate: Matematica, Geografia Astronomica, Italiano, Storia Dell’Arte, Filosofia, Letteratura Inglese
Italiano: Giacomo Leopardi, L’Infinito
Arte: Escher, rappresentare l’infinito
Filosofia: Friedrich Nietzsche, Così Parlò Zarathustra
Inglese: William Butler Yeats, Sailing To Byzantium
Chi prenderà in mano questa "tesina", se vogliamo chiamarla così, probabilmente si troverà a pensare che l’infinito, di per se, sia un argomento forse banale e già sfruttato. Che poi sarebbe la stessa cosa che ho pensato io da principio. La trattazione, tuttavia, può avvenire attraverso molteplici (infinite, direi) vie: si può dare un’impostazione umanistica, scientifica, linguistica, artistica al lavoro che si svolge, a seconda della personalità e delle peculiarità del singolo individuo. E ognuna di queste impostazioni, fintanto che il lavoro resterà originale, avrà differenti caratteristiche.
Quella scientifica è una delle più interessanti e, per certi versi, innovative. La "promessa", tuttavia, si è rivelata più difficile del previsto da mantenere, vuoi per il poco tempo a disposizione, vuoi per l’estrema complessità dell’argomento. E questo mi ha costretto a dirottare il mio lavoro su un’analisi forse più superficiale ma al contempo più allargata.
Divagazioni a parte, l’infinito è uno dei temi che quest’anno, indipendentemente dal lavoro scolastico, ho avuto modo di affrontare più volte, attraverso letture, riflessioni personali e con alcuni miei cari "compagni di pensiero", addirittura attraverso i miei hobby (cosa che mai mi sarei aspettato). La mia decisione non è quindi solo legata all’apparente semplicità (come in un primo momento mi era parso) di questa idea, ma anche al mio stupore nel notare come un qualcosa che io avevo sempre considerato puramente matematico (non dico anche filosofico perché, si sa, matematica e filosofia sono quasi la stessa cosa) potesse entrare in un modo o nell’altro in ogni campo dell’esistenza.
Alla stessa maniera, la scelta di iniziare la trattazione proprio dalla matematica è volta allo scopo di dimostrare un‘idea che mi ha praticamente "perseguitato" durante il periodo del liceo: all’interno della mia classe sono il solo a cui piace la matematica intesa come materia scolastica, e sono il solo che proseguirà gli studi iscrivendosi proprio in quella facoltà. Ogni volta che esprimo questo mio desiderio, la maggior parte degli ascoltatori mi guarda allibita quasi a chiedersi quale specie di bestia rara si ritrovi davanti. Più volte sento dire che la matematica non serve a niente, che è inutile, che in fondo basta saper fare le operazioni di base per procedere nella vita senza problemi. Ma io so che non è così. Innanzitutto, la nostra società, di stampo economico/capitalistico, si basa interamente sulla matematica: portando un esempio che potrebbe sembrare stupido, anche il prezzo della benzina che paghiamo settimanalmente quando facciamo il pieno è il risultato di una relazione matematica tra i fattori domanda – produzione – periodo. Il funzionamento dei computer è il risultato della scrittura di un codice "binario" proprio della matematica, i programmi, i videogiochi, persino i video e le immagini disponibili su internet sono il risultato di algoritmi complessi studiati allo scopo di raccogliere e sintetizzare i dati nella maniera più semplice e veloce possibile. Eppure la matematica non è solo questo.
Fonti internet:
• http://www.wikipedia.org , l’enciclopedia gratuita online
• http://www.vialattea.net , il sito per la divulgazione scientifica
• http://images.google.it , ricerca immagini Google
• http://www.deviantart.com , dove l’arte incontra l’applicazione
Fonti testuali:
• AA.VV., I Filosofi e le Idee, Mondadori
• AA.VV., Books and Bookmarks, Loescher
• Escher M. C., Grafica e Disegni, Taschen
• Lotman e Uspenskij, Tipologia della Cultura, Bompiani
• Nietzsche Friedrich, Così Parlò Zarathustra, Mursia
Scarica la tesina L’infinito
IL FILE CONTENENTE LA TESINA E’:TESINA UFFICIALE. LA TESINA è STATA SVILUPPATA IN POWER POINT, LE SLIDE SONO CONNESSE TRAMITE COLLEGAMENTI IPERTESTUALI (PAROLE SOTTOLINEATE)
Materie interessate: italiano,storia,inglese
Scarica la tesina:
https://www.matematicamente.it/tesine/Michela_Latorre-In_evoluzione_l_informatica.zip
La tesi tratta tutte le materie interessate alla maturità, riportando degli esempi reali nelle materie d'indirizzo. N.B. Per una visualizzazione ottimale bisogna impostare lo sfondo con una risoluzione di 1024*768; Estrarre la cartella Tesi di maturità presente nel file zip in "C:"; Successivamente bisogna aver installato il software Microsoft Web Matrix presente nel file .zip, poichè la tesi è stata realizzata tramite pagine .aspx e la tool Web Matrix simula l'architettura server side; Una volta installato è possibile aprire la pagina index.aspx tramite il software, e cliccare sul tasto play presente nella barra dei comandi. Nella materia Informatica ci sarà un link che aprirà un database e per effettuare alcune prove bisogna inserire user e pwd nella seconda e terza query (Es. User: "0885410001", PWD: "112233"). Se dovessero esserci ulteriori problemi di visualizzazione, come ultima procedura dovete disporre di Microsoft Office 2007 perché sono state effettuate delle opportune conversioni in html in alcune pagine. Buona visione.
Materie interessate: Italiano (Luigi Pirandello); Storia (Il Fascismo in Italia); Elettronica e Sistemi (Sistema di trasmissione telefonica analogica e digitale); Inglese (DBMS); Informatica (Database, più esempio); Matematica (Studio di funzione, più esempio); Calcolo (Analisi serie storiche, più esempio)
Scarica la tesina:
https://www.matematicamente.it//tesine/Alessandro_Pontrelli-Righi_telephon.zip
Scarica la tesina:
https://www.matematicamente.it/tesine/Janka_Spallino-I_mass_media.zip
Nella realizzazione della mia tesina, ho voluto approfondire un periodo molto particolare della storia economica americana e mondiale: la rivoluzione industriale di massa. Tale importante rivoluzione scoppia in America nei primi anni del Novecento, periodo di grande prosperità per tutta l economia americana. Siamo in corrispondenza dei cosiddetti Anni ruggenti , gli anni del Jazz e degli enormi grattacieli, dei primi movimenti femministi e delle leggi sul proibizionismo.
Scarica la tesina:
https://www.matematicamente.it/tesine/Silvia_Moraschi-Gli_anni_ruggenti.zip