Autore: stan
Cenni di probabilità
Lo spazio campionario per un esperimento è l’insieme di tutti i suoi possibili esiti. Per esempio, se l’esperimento è il lancio di due di dadi e si rappresentano le coppie di numeri che escono sulle facce superiori, {5, 2} è un possibile esito e appartiene allo spazio campionario, ma {1, 7}, {-4, 3}, {4, 4, 4}, {a, 1} e {3/4, 3/4} non sono esiti possibili.
Sia S uno * spazio campionario * di eventi. Siano A e B eventi in S.
Sia P(A) la probabilità dell’evento A. Allora:
Due eventi sono mutualmente esclusivi se essi non possono accadere contemporaneamente. Per esempio, gli eventi estrai una figura e estrai picche non sono mutualmente esclusivi, dal momento che possiamo estrarre il re di picche, ma gli eventi estrai una carta rossa e estrai picche sono mutualmente esclusivi.
Sia f la frequenza di un evento A e n sia la dimensione del campione. La probabilità dell’evento A è
In una scuola superiore, viene selezionato un campione di 500 studenti e 392 di questi studenti sanno usare il computer. Qual è la probabilità che uno studente scelto a caso dal campione sappia usare il computer
La probabilità è la frequenza relativa degli studenti nel campione che sanno usare il computer rispetto al numero degli studenti del campione :
Sono lanciate tre monete. Calcola la probabilità che esca testa esattamente una volta.
Calcola la probabilità di vincere una lotteria se la combinazione vincente è formata da sei numeri estratti a caso dai numeri da 1 a 49.
Lo spazio campionario degli esiti ugualmente probabili è il numero di combinazioni di 49 numeri presi 6 alla volta. Solamente una combinazione può essere quella vincente.
La dimensione dello spazio campionario si trova usando la formula per le combinazioni:
La probabilità di essere colpito da un fulmine è maggiore di quella di vincere tale lotteria.
Basandosi sui dati I.S.T.A.T 20 contribuenti scelti da un campione di 750, che hanno dichiarato un reddito inferiore a £ 20000000, subiscono una verifica ogni anno. Calcola la probabilità di una revisione se il reddito riportato è inferiore a £20000000.
P(A o B) = P(A) + P(B) – P(A e B)
Due eventi sono detti indipendenti se l’occorrenza di uno di essi non ha effetti sulla probabilità del verificarsi dell’altro.
Lancia due dadi. Qual è la probabilità di avere un 6 sul primo dado E un 6 sul secondo dado? Qual è la probabilità di ottenere un 6 sul primo dado O un 6 sul secondo dado?
Poiché gli esiti dei due dadi sono eventi indipendenti, la probabilità di avere un 6 sul primo dado e un 6 sul secondo dado, per la regola della moltiplicazione, è
la probabilità di ottenere un 6 sul primo dado o un 6 sul secondo dado, per la regola di addizione, è
Si estrae una carta da un mazzo di 52 carte da gioco. Qual è la probabilità che la carta sia di fiori OPPURE una figura?
Sia A l’evento di estrarre una carta di fiori e B sia l’evento di estrarre una figura.
Ci sono 13 fiori, così P(A) = .
Tre carte — fante, donna e re di fiori — sono contemporaneamente fiori e figure. Così P(A e B)= .
Per la regola dell’addizione, la probabilità di estrarre una carta di fiori o una figura è
Se la probabilità che nevichi il Martedì è 0.3 e la probabilità che nevichi il Venerdì è 0.9, qual è la probabilità che nevichi sia il Martedì che il Venerdì?
Se supponiamo che l’eventualità che nevichi in un dato giorno sia un evento indipendente, la probabilità che nevichi sia il Martedì che il Venerdì è il prodotto delle probabilità.
Siano A e B eventi in uno spazio di probabilità. La probabilità condizionata di A, dato che l’evento B è accaduto, è denotata con P(A|B) . Vale la relazione
Siano A 1 , A 2 … A n eventi mutualmente esclusivi la cui unione sia uno spazio campionario S. Sia E un evento arbitrario di S tale che . Allora
P(A 1 |E) = P(A 1 )*P(E|A 1 )/(P(A 1 )*P(E|A 1 ) + P(A 2 )*P(E|A 2 ) + … +P(A n )*P(E|A n ))
Lancia un dado rosso e un dado verde. Dato che la somma dei dadi è minore di 4, qual è la probabilità che il dado verde sia 1 ?
Rappresentiamo con (g, r) l’esito sul dado verde e sul dado rosso. La dimensione dello spazio campionario è 36. L’evento somma dei dadi minore di 4 è costituito da
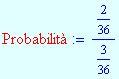
In una famiglia con due figli è noto che c’è almeno un maschio. Qual è la probabilità che entrambi i figli siano masch i ?
Lo spazio degli eventi è { MM, MF, FM, FF }. La probabilità che ci sia almeno un maschio . La probabilità che entrambi i figli siano maschi è
. La probabilità che entrambi i figli siano maschi sapendo che già uno sia almeno un maschio è :
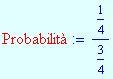
In una classe universitaria di matematica, il 5% degli uomini e il 2% delle donne hanno più di 22 anni. Il 70% degli studenti nella classe sono donne. Se uno studente scelto a caso ha più di 22 anni, qual è la probabilità che lo studente sia una donna ?
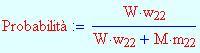
Proprietà delle soluzioni: innalzamento ebullioscopico
Proprietà delle soluzioni: abassamento crioscopico
Cruciverba – Novembre 2007
 Un cruciverba a sfondo matematico, molte delle definizioni riguardano la matematica. È per i più bravi. Si può fare on line oppure stampare il foglio e risolverlo con la penna.
Un cruciverba a sfondo matematico, molte delle definizioni riguardano la matematica. È per i più bravi. Si può fare on line oppure stampare il foglio e risolverlo con la penna.
Galleria di frattali di Marco Bono
{gallery}galleries/frattali/marco_bono{/gallery}
Galleria di frattali di Alessio Troni
 Una fotogallery di frattali
Una fotogallery di frattali
{gallery}galleries/frattali/alessio_troni{/gallery}
Equazioni parametriche con Derive
Le reti
Guida all’installazione e uso di Microsoft NetMeeting
Crucinumero: Misure da pin up
Compito in classe I liceo scientifico PNI
Compito in classe I liceo scientifico PNI
Compito in classe I liceo scientifico PNI
Compito, classe I, LS PNI: frazioni, percentuali, insiemi, sistema binario
Compito in classe IV liceo scientifico PNI
Compito in classe III liceo scientifico PNI
Compito in classe II liceo scientifico PNI
Compito in classe II liceo scientifico PNI
Compito in classe II liceo scientifico PNI
Compito in classe II liceo scientifico PNI
Compito in classe II liceo scientifico PNI
Compito in classe II liceo scientifico PNI
Compito in classe II liceo scientifico PNI
Recupero debiti classe II liceo scientifico PNI
Compito in classe II liceo scientifico
Compito in classe I liceo scientifico PNI
Compito, classe I, liceo scientifico PNI: equazione frazionaria, equazione letterale, geometria
Compito, classe I, liceo scientifico: calcolo letterale, geometria, informatica
Compito in classe I liceo scientifico
Compito in classe I liceo scientifico
Compito in classe I liceo scientifico
Giochino con i numeri binari
Il problema del quattro
 Una storia a fumetti liberamente tratta dal libro di E. Bencivenga, La filosofia in trentadue favole
Una storia a fumetti liberamente tratta dal libro di E. Bencivenga, La filosofia in trentadue favole

Angoli
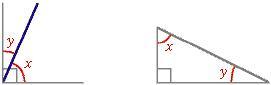

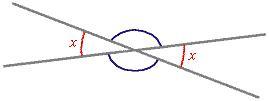
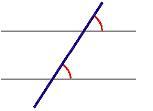
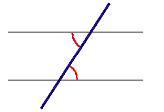

Angoli coniugati esterni
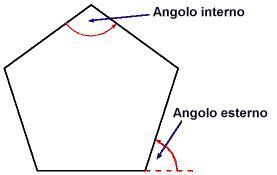
Trova la somma degli angoli interni di un esagono e di un poligono con 13 lati
n non appare in questa espressione, quindi la somma degli angoli esterni è indipendente dal numero di lati del poligono.
2,7182818284590, numero di Nepero o di Eulero?
2,7182818284590 … numero di Nepero o di Eulero? di Erman Di Rienzo (novembre 2000)
|
|
|
|
|
Napier o Neper John, latinizzato Neperus, italianizzato Nepero (1550-1617) |
Euler Leonhard, italianizzato Eulero |
Considerate la vostra semenza: fatti non foste a viver come bruti, ma per seguir virtute e canoscenza. (Dante: Inf.-XXVI-118) Introduzione
Il numero "e" è una delle più importanti costanti della Matematica.
Se andiamo con la memoria al primo incontro con questo numero, ci ricorderemo del nostro testo di algebra delle medie superiori, che dopo averci definito il logaritmo e le sue proprietà ci diceva all’ incirca:
" … I sistemi di logaritmi di uso comune sono due:
1) I logaritmi volgari, o decimali o di Briggs, a base 10, che sono quelli che si adoperano nelle applicazioni pratiche e che sono contenuti nelle Tavole;
2) I logaritmi naturali o neperiani, la cui base è un numero irrazionale, indicato con "e", uguale approssimativamente a 2,718… ".
In precedenza, il nostro manuale di algebra, ci aveva detto dell’ esistenza dei numeri irrazionali: quei numeri nella cui parte decimale le cifre si seguono quasi casualmente, senza nessuna regola se non quella che definisce il numero stesso. Al contrario, i razionali, dopo un certo numero di cifre decimali, hanno tutti zeri o sequenze di cifre che si ripetono periodicamente; possono essere messi sotto forma di frazione con numeratore e denominatore interi, da cui il nome dal latino ratio , nel significato di rapporto. Ma ratio significa anche ragione; come dire che razionali sono quei numeri sui quali si può ragionare, mentre irrazionali sono numeri non ragionevoli, stravaganti, quasi folli. Come un monito: attenzione a sbarcare su quel pianeta! Nulla vi è di predicibile.
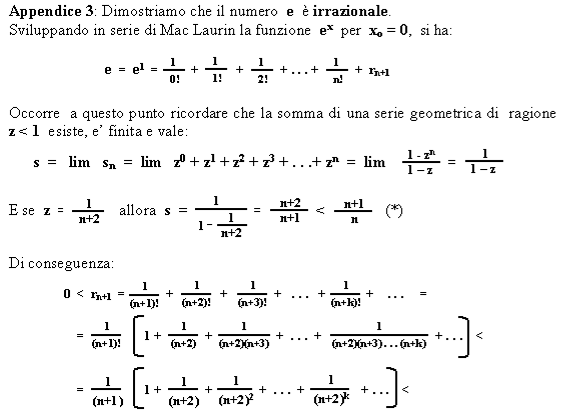
Il nostro numero per un istante ci dà la speranza della razionalità: dopo la prima cifra decimale si ripete la sequenza 1828 . La speranza è presto frustrata; dopo la prima ripetizione le cifre riprendono a seguirsi in modo apparentemente casuale: 2,7182818284590 … Anche di esso è stata dimostrata la natura irrazionale (appendice3).
Come se non bastasse, il numero viene detto anche trascendente perché non c’è un’equazione a coefficienti razionali che lo ammetta come soluzione: si sfiora la teologia.
Più avanti negli studi il nostro numero, indicato con e, viene introdotto come limite della successione:
(1 + 1/1)1 , (1 + 1/2)2 , (1 + 1/3)3 , …, (1 + 1/n)n , …
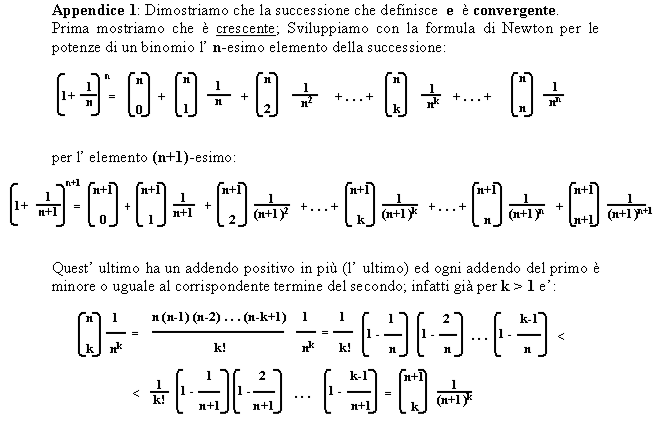
Ci viene dimostrato che essa è crescente essendo ogni termine maggiore del precedente, limitata superiormente essendo ogni termine minore di 3 e quindi, per un noto teorema sulle successioni, convergente cioè che esiste un numero al quale la successione tende ad avvicinarsi sempre di più. Più tecnicamente, in numero la cui differenza con un elemento della serie può essere reso minore di qualsivoglia quantità (una volta si diceva piccolo a piacere) scegliendo opportunamente n; questo numero è proprio il nostro (appendice1).
Un procedimento analogo si può applicare per definire pigreco: quattro volte l’ integrale tra 0 e 1 della funzione f(x) = 1 / (1 + x2 ). Proseguendo riusciremmo anche a dimostrare che incidentalmente esso è anche il rapporto tra la lunghezza della circonferenza e il diametro del cerchio. La definizione è certamente rigorosa, ma non tiene conto del profondo legame tra il numero e il problema della misurare della circonferenza.
Anche il numero "e" è profondamente legato a problemi reali; è continuamente sotto i nostri occhi, scritto nel meraviglioso libro della natura nel quale la matematica dovrebbe insegnarci a leggere. Esso infatti è presente ogni qual volta un fenomeno di crescita (o di decrescita) dipende dal tempo e dalla grandezza che cresce (o decresce). Facciamo qualche esempio: una popolazione di batteri in un terreno illimitato di cultura: più batteri sono presenti più velocemente cresce la popolazione. Più cresce la popolazione, più batteri hanno la possibilità di generare, più rapidamente di prima cresce la popolazione.
Più evidente è il caso di un conto in banca : supponiamo di avere un certo capitale A depositato al tasso di interesse (semplice) annuo di x per cento, cioè al tasso assoluto di r = x/100.
Dopo un anno il nostro capitale è diventato A1 = A×(1+r). Dopo un altro anno: A2 = A1 ×(1+r) = A×(1+r)2 , dopo tre anni A3 = A×(1+r)3 e dopo n anni An = A×(1+r)n . La crescita esponenziale è spiegata dal fatto che anche gli interessi maturati entrano nel capitale e fruttano altri interessi.
Ma dopo mezzo anno? Sembrerebbe, banalmente, che il capitale si sia rivalutato della metà di r, ma non è così perché se così fosse dopo n anni sarebbe: An =A×(1+nr) e non An = A×(1+r)n .
Supponiamo allora di aver concluso con la banca un accordo secondo il quale l’ interesse matura ogni sei mesi (1/2 di anno) con un tasso di r/2. Dopo un semestre il capitale sarà diventato A1/2 = A×(1+r/2) e dopo un anno A1 = A×(1+r/2)2 .
Se concordassi la maturazione ogni quadrimestre (1/3 di anno) al tasso di r/3 dopo un trimestre avrei A1/3 = A×(1+r/3) e dopo un anno A1 = A×(1+r/3)3 .
Se gli interessi maturassero ogni 1/n di anno al tasso di r/n dopo ogni m frazioni di anno avrei Am/n = A(1+r/n)m e dopo un anno A1 = A×(1+r/n)n .
Per una maturazione continua (interesse composto) basterebbe passare al limite per n tendente all’ infinito e dopo un anno avrei un capitale di: A1 =Alim(1+r/n)n
Se fosse r = 1 questo limite sarebbe proprio e . Se r è diverso da 1 con il cambio di variabile m = n/r si ha:
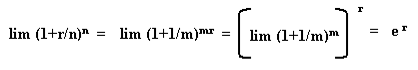
Quindi dopo un anno sarà A1 = Aer e dopo t anni (con t non necessariamente intero): At = Aet r .
Osserviamo che il numero e è emerso in un modo che direi "naturale", non è stato introdotto artificiosamente.
Presenze di e si riscontrano in ogni campo delle scienze. Propongo solo alcuni casi:.
In Termodinamica la legge di Stephan-Boltzmann: lo spettro di emissione (= poten-za per unità di lunghezza d’ onda in funzione della lunghezza d’ onda) del corpo nero per unità di superficie ad una certa temperatura assoluta T è dato da:
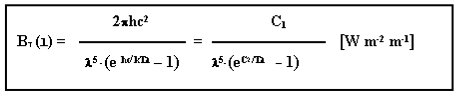
In Fisica Nucleare il decadimento radioattivo: Se al tempo t0 = 0 sono presenti N0 atomi instabili al tempo t ne rimarranno N, dato da:
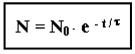
dove la lettera greca tau è una costante temporale caratteristica del tipo di atomo detta "vita media" o "emivalore" di quell’ atomo.
In Geometria Analitica : una "innocente" iperbole equilatera di equazione y = 1/x:
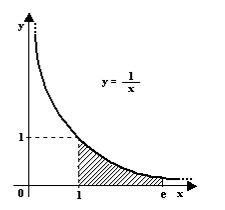
Sappiamo che passa per il punto (1, 1). Ma partendo da x = 1 quale base dobbiamo considerare perché l’ area sotto la curva (tratteggiata) abbia valore unitario?
Ebbene, manco a dirlo, proprio il tratto di ascissa tra 1 ed e.
In Analisi Combinatoria il numero di "dislocazioni": Sia dato un insieme di n oggetti distinti. E’ noto che il numero delle disposizioni (combinazioni ordinate senza ripetizione) degli n oggetti è dato da n!. Tra queste disposizioni molte hanno in comune almeno un oggetto nella stessa posizione; altre invece non ne hanno alcuno in comune.
Facciamo un esempio: dato un insieme di tre oggetti: a1, a2 e a3, le disposizioni possibili sono 3! = 6:
(a1, a2, a3), (a1, a3, a2), (a2, a1, a3), (a2, a3, a1), (a3, a1, a2) e (a3, a2, a1).
Di queste solo due: (a2, a3, a1) e (a3, a1, a2) non hanno alcun oggetto nella stessa posizione. Quindi avremo 2 disposizioni di questo tipo su 6; il rapporto disposizioni/dislocazioni è 6/2=3.
Se gli oggetti fossero quattro, avremmo 4! = 24 disposizioni, ma di queste solo 9 del nostro tipo; il rapporto disposizioni/dislocazioni è 24/9 = 2,666…. Per n = 5 questo rapporto vale 5! / 44 = 120 / 44 = 2,7676….
Nel caso di n oggetti ci viene in aiuto un teorema di Eulero che afferma che il numero di dislocazioni è:
Dn = n!×[ 1 – 1/1! + 1/2! – 1/3! + . . . + (-1)n×(1/n!)],
ed essendo n! il numero delle disposizioni si ha che il rapporto tra disposizioni e dislocazioni è:
R =1 / [1 – 1/1! + 1/2! – 1/3! + . . . + (-1)n × (1/n!)].
Ma quanto vale questo rapporto quando n tende all’ infinito? Ebbene, vale proprio e.
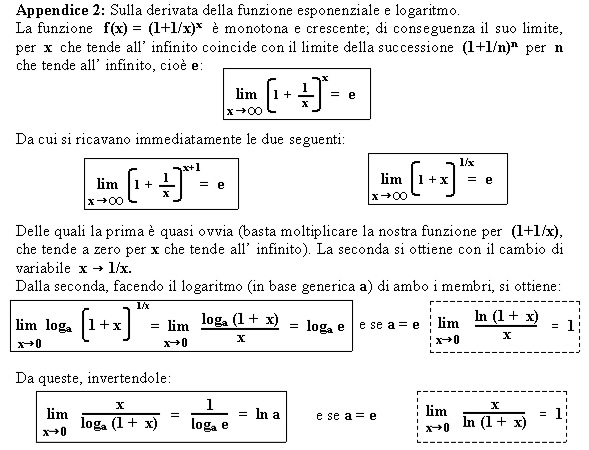
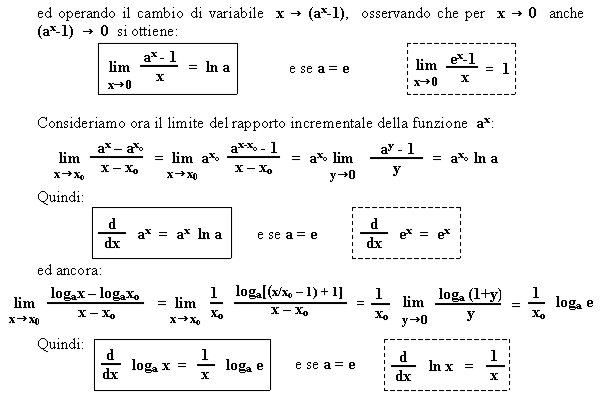
In Analisi matematica la funzione esponenziale ax : la sua derivata è ax × lna, dove con ln si è indicato il logaritmo naturale (quello con base e). Pertanto la derivata della funzione esponenziale ex è la funzione ex stessa, e questo è l’ unico caso in matematica di una funzione che ha per derivata se stessa.
Analogamente per la funzione logaritmo loga x: la derivata è la funzione ![]()
Ne segue che la derivata di ln x è semplicemente 1/x.
Per gli approfondimenti si rinvia all’ appendice 2.
In Teoria dei numeri : consideriamo i numeri naturali: 1, 2, 3, … , n, … Per ogni n consideriamo la media aritmetica An e quella geometrica Gn di tutti i numeri fino ad n:
An= (1+2+3+…+n) / n = (n+1)/2
Gn = (1*2*3*…*n)1/n = (n!) 1/n
Ebbene il rapporto tra queste due medie, quando n tende all’ infinito, tende proprio ad e.
Ed ancora, per ogni n consideriamo tutti i numeri primi minori o uguali ad n che indichiamo con pi ; la media geometrica di tutti questi np primi per ogni n, tende ad e quando n tende all’ infinito.
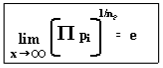
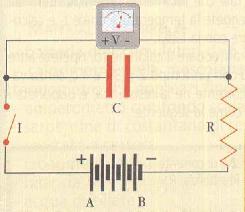
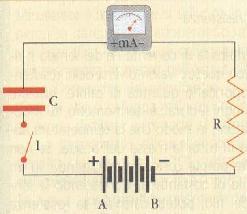
In Elettrotecnica : la scarica di un condensatore su una resistenza. Se un condensatore di capacità C, carico all’istante t = 0 alla tensione Vo , si scarica su una resistenza R, la sua tensione varia nel tempo nel modo descritto dalla funzione:
V(t) = V o × (1 – e-t /T ) con T = R/C
Come per il primo, in tutti gli esempi successivi riportati il numero e emerge per così dire spontaneamente, in modo "naturale".
Ma veniamo alla storia del numero attraverso i suoi principali protagonisti: Nepero ed Eulero.
John Napier
Altrimenti noto come Neper, o in italiano Nepero, non era un matematico di professione. Nacque in Scozia nel 1550 ed a soli 13 anni fu iscritto alla St. Andrews University dove si appassionò alla Teologia; ma completò gli studi all’estero forse a Parigi. Tornò in Scozia nel 1571 dove si dedicò alla cura delle proprietà della famiglia, in particolare all’agricoltura verso la quale ebbe un approccio scientifico sperimentando vari tipi di concimi.
Essendo un fervente religioso, assertore della chiesa anglicana, fu coinvolto nelle dispute di religione che infuriarono al suo tempo. In un suo "Plaine Discovery of the Whole Revelation of St. John" del 1593, interpretò l’Apocalisse in funzione antiromana, identificando nel Papa l’ Anticristo profetizzato da S.Giovanni. In quel tempo in Inghilterra era diffuso il timore di un’invasione da parte di nazioni cattoliche.
Ben presto però abbandonò la Teologia per dedicarsi a discipline scientifiche come la meccanica, in particolare la balistica, e l’ astronomia.
La matematica per lui fu solo un hobby, per il quale peraltro non aveva molto tempo; che sia questo il motivo per il quale si dedicò con tanto impegno a trovare un metodo per eseguire più velocemente i calcoli? Già da tempo erano note formule, che oggi chiamiamo di prostaferesi, che permettono di calcolare il prodotto di funzioni goniometriche (seno e coseno) attraverso la loro somma. Si chiese se fosse possibile estendere questa possibilità ad ogni tipo di moltiplicazione. Certo aveva notato che il prodotto di due potenze aventi la stessa base è uguale alla potenza con indice la somma degli indici [ab × ac = ab+c ]. Ipotizzò quindi che trasformando tutti i numeri in potenze con la stessa base si sarebbe potuto trasformare i prodotti tra i numeri in più facili somme tra gli indici. Aveva inventato il logaritmo , come egli stesso aveva battezzato.
Pubblicò i risultati della sua ricerca nel 1614 in un famoso "Mirifici logarithmorum canonis descriptio" in cui afferma di sperare che il suo metodo possa far risparmiare tempo a coloro che eseguono calcoli liberandoli dalla possibilità di fare "viscidi errori"; nella moltiplicazione, si sa, un piccolo errore in punti strategici, ad es. un errore di riporto sulle cifre più significative, può avere effetti catastrofici sull’esito finale del calcolo. Ed in effetti fu così; fino alla recente invenzione di calcolatori e calcolatrici elettroniche l’uso dei logaritmi ha costituito un vero sollievo per chi doveva eseguire calcoli. Chi ricorda il "regolo calcolatore" frutto immediato della teoria dei logaritmi? Lo stesso Laplace, parlando di Nepero, affermò, con riferimento all’ astronomia, che "… avendone ridotto il lavoro, egli aveva raddoppiato la vita degli astronomi".
Il suo lavoro fu, successivamente, perfezionato con l’ aiuto di Henry Briggs.
Morì nel 1617, ed anche per lui non mancarono le solite leggende che lo volevano in contatto col diavolo. Si diceva che fosse solito passeggiare in camicia e berretto da notte o andare in giro con un gallo ricoperto di fuliggine. D’altra parte non è sorprendente che un uomo di tale intelletto apparisse strano ai suoi contemporanei e che, considerando la superstizione di quei tempi, strane storie circolassero sul suo conto.
Nel suo libro per la prima volta viene citato il numero e, ma rimase poco più che una citazione; lo usò infatti solo per introdurre i logaritmi. A quel tempo l’ algebra non era sufficientemente sviluppata e Nepero per esplicitare la sua intuizione dovette ricorrere ad una interpretazione fisico-geometrica:
Si considerino un segmento AB ed una semiretta Ox; un punto P sul segmento ed uno P’ sulla semiretta partono contemporaneamente da A e da O rispettivamente, inizialmente con la stessa velocità proporzionale alla lunghezza del segmento AB, però mentre P’ prosegue a velocità costante, P rallenta continuamente di modo che la sua velocità è sempre proporzionale al resto del segmento che gli resta da percorrere. Il logaritmo dello spazio percorso da P è uguale allo spazio percorso da P’. Lo spazio percorso da P’ in pratica rappresenta il tempo t ed il punto P non raggiungerà mai l’ estremo B del segmento.
A quei tempi le equazioni differenziali non erano state neanche definite, men che mai risolte, ma oggi sappiamo che il moto del punto P è un esponenziale smorzato del tipo: s = so (1 – e-t / T ) in cui s è lo spazio che resta da percorrere, so è la lunghezza del segmento AB, e T la costante di tempo che dipende dalla proporzione della velocità con lo spazio che resta da percorrere.
Con facili passaggi si ottiene: e-t / T = (s – so ) / so , da cui si vede che il tempo è il logaritmo con base 1/e dello spazio.
Ma nel prosieguo non utilizzò questa come base dei suoi logaritmi, preferendogli una strana costante K = 1-10-7 , probabilmente perché meglio consentiva le interpolazioni.
Suo invece il nome di logaritmo dato a questa trasformazione, senza però darne giustificazione. Sono state fatte varie ipotesi; certamente il nome deriva da due vocaboli greci logos e aritmos. Sul secondo non dovrebbero esserci dubbi giacché significa esclusivamente "numero". Sul primo le cose si complicano; esso infatti ha molti significati a seconda del contesto di utilizzo: può significare "parola" o "discorso" (da cui il nostro "dialogo"), per arrivare fino a "pensiero" o "ragione" (da cui la nostra "logica"); in qualche caso anche "proporzione", in questo riconducibile al latino "ratio" nel senso di "rapporto". Probabilmente Nepero ha chiamato così i logaritmi perché danno una misura della "proporzione tra i numeri".
E’ improbabile, ma mi piace fantasticare che Nepero abbia voluto invece intendere con "logaritmo" il "ritmo del pensiero"; immaginiamo per un istante il numero 10 ed il numero 100; i due numeri ci appaiono distanti. Immaginiamo ora i numeri 100 e 1000; anche questi ci appaiono distanti ma della stessa quantità. Ed analogamente per 1000 e 10000, per 1 milione e 10 milioni e così via. Ebbene la differenza tra il logaritmo di 10 e quello di 100 è la stessa che c’è tra il logaritmo di 100 milioni e quello di 1 miliardo. In conclusione quando pensiamo a quantità misurabili il nostro pensiero diventa logaritmico.
Anche molti nostri sensi sono logaritmici. Un suono ad esempio ci appare di certa intensità; per ottenere un sensazione doppia del primo occorre produrre un altro suono quattro volte più potente del primo. In termini matematici la sensazione uditiva cresce col logaritmo della potenza sonora. Ed infatti per la misura dell’ intensità dei suoni si usa il decibel che è un’unità logaritmica.
Analogamente la sensazione visiva: per raddoppiare la sensazione visiva occorre una sorgente luminosa quattro volte più potente (22 = 4), per triplicarla una potenza otto volte maggiore (23 = 8) e così via. Anche l’occhio quindi ha una sensibilità per così dire logaritmica.
Leonhard Euler
Meglio conosciuto in italiano come Eulero. Non vi è dubbio che sia stato uno dei più grandi matematici di tutti i tempi, certamente il più grande del suo secolo, il Settecento, il "secolo dei lumi".
Il contributo di Eulero alla matematica è stato così importante ed esteso che espressioni come "la formula di Eulero", "il teorema di Eulero", "la congettura di Eulero" o " la costante di Eulero" possono avere significati diversi in diversi contesti.
La sua opera consta di quasi 90 opere in ogni settore dello scibile scientifico, molte delle quali prodotte negli ultimi anni della sua vita quando era ormai cieco.
Nacque il 15 aprile 1707 a Basilea, dove la famiglia si era rifugiata per sfuggire alle guerre di religione, e dove studiò alla scuola del grande matematico Johann Bernoulli, del quale fu l’ allievo preferito; il che già non era cosa facile per l’ indole sospettosa ed invidiosa del maestro; pare che gli dedicasse una lezione privata ogni sabato pomeriggio. Anche successivamente, quando Eulero si trasferì all’ estero, la corrispondenza fra il vecchio maestro e l’allievo fu sempre intensa e cordiale, fino al riconoscimento della superiorità dell’allievo ed alla sua definizione di "Principe dei matematici".
Nel 1727 si trasferì a San Pietroburgo alla corte di Caterina I, grande imperatrice di tutte le Russie, al seguito del figlio di Johann, Daniel Bernoulli che era stato nominato professore di matematica presso l’ Imperiale Accademia delle Scienze; nel 1733 assunse la cattedra di Bernoulli e la tenne fino al 1741, quando fu nominato professore di Matematica e Fisica all’ Accademia di Berlino. A Berlino rimase fino al 1766, quando ritornò alla sua San Pietroburgo dove rimase fino alla morte nel 1873. Così vasta fu la sua produzione che l’ Accademia delle Scienze continuò a pubblicarne le opere per più di trent’anni dopo la morte. La sua "Introductio in Analisyn Infinitorum" in due volumi del 1748 è considerata la base della moderna analisi matematica.
Leggendarie erano la sua memoria e capacità di concentrazione. Si narra che fosse capace di recitare l’ intera Eneide parola per parola, che avesse scritto la maggior parte dei suoi lavori in presenza dei figlioletti che giocavano e che fosse in grado di riprendere un discorso interrotto anche a distanza di tempo.
Se a Nepero può essere attribuita la scoperta del nostro numero, ad Eulero il merito di averlo approfondito e reso popolare.
Fu Eulero per primo ad indicarlo con la lettera "e". In verità Eulero ha dato un nome a molte costanti ed operatori matematici, nomi ancora oggi in uso; fu lui per primo a usare il simbolo "pi greco" (in onore di Pitagora), con "i" l’unità immaginaria /-1 , con f(x) l’ operatore "funzione", con sigma la sommatoria e tante altre ancora oggi in uso.
Ci si chiede spesso perché abbia scelto la lettera e per il nostro numero. Conoscendo il suo carattere schivo e la sua modestia è da escludere che lo abbia scelto perché iniziale del suo nome; né poteva autocelebrarsi uno che dimenticava perfino di pubblicare i suoi lavori, tanto che spesso qualche collega o qualche allievo successivamente se ne faceva merito. Più probabilmente e casualmente perché è la prima lettera dopo le abusate a, b, c e d dell’ algebra e prima di f e g che servivano per le funzioni, e lontano dai k, l, m ed n della teoria dei numeri (naturali ed interi), o forse perché è l’ iniziale di "esponenziale".
Ma considerando lo sviluppo che ha dato all’ indagine matematica, a tutti i matematici è sempre piaciuto pensare che "e" fosse proprio l’ iniziale del suo nome.
Circa il numero e, era già noto l’elevazione a potenza con base ed esponente reali; erano stati anche introdotti i numeri complessi, ma non era noto come estendere a questi numeri l’ operazione di elevazione a potenza.
Partiamo da una base reale a: per elevarlo a potenza con indice complesso z = x + iy per una nota proprietà delle potenze può porsi az = ax . aiy . Per il primo addendo non ci sono problemi; per il secondo occorre definire il significato di un numero reale elevato ad un numero immaginario. Eulero attraverso manipolazioni sulle serie infinite ottenne la formula che permette questa definizione. Egli aveva ottenuto per e la seguente espressione come somma di una serie:
e = 1/0! + 1/1! + 1/2! + 1/3! + . . . + 1/n! + . . .
e più in generale per la elevazione a potenza con base e ed esponente x la seguente:
ex = xo /0! + x1 /1! + x2 /2! + x3 /3! + . . . + xn /n! + . . .
della quale la prima è un caso particolare (x = 1), ed in cui sostituendo al reale x un immaginario iy si otterrebbe:
eiy = (iy)o /0! + (iy)1 /1! + (iy)2 /2! + (iy)3 /3! + . . . + (iy)n /n! + . . . =
= i0 * yo /0! + i1 * y1/1! + i2 * y2 /2! + i3 * y3 /3! + . . . + in * yn /n! + . . . =
= (yo /0! – y2 /2! + y4 /4! + …) + i * (y1 /1! – y3 /3! + y5 /5! + . . . )
in quest’ ultimo passaggio si attribuisce all’ unità immaginaria i la stessa proprietà della potenza dei numeri reali per la quale elevandola a 0 si ottiene l’ unità; inoltre si sono separate le potenze pari da quelle dispari sviluppando le potenze dell’ unità immaginaria:
i1 = i, i2 = -1, i3 = -i, i4 = 1, i5 = i, i6 = -1, . . .
Ma le due serie in parentesi sono lo sviluppo in serie delle funzioni cos y e sen y da cui la bellissima formula:
eiy =cosy+isiny
da lui individuata e che porta il suo nome. Essa resta uno dei più importanti e meno intuitivi risultati della matematica.
La formula fu il "cavallo di Troia" per portare la funzione potenza nel campo complesso. Con essa infatti è facile mostrare che ogni numero complesso z = x + iy di modulo r = (x2 + y2 )1/2 e di argomento q = arctg (y/x) può essere espresso come:
z = r eiq
che permette di definire il logaritmo naturale di un numero complesso:
ln z = ln (r . ei q ) = ln r + ln ei q = ln(r) + i q
da cui quindi è facile passare alla potenza con base complessa b ed esponente complesso z:
bz = ezln(b)
Se nella formula di Eulero si dà ad y il valore pigreco (PG), ricordando che cos(PG) = – 1 e che sen(PG) = 0 si ottiene la bellissima relazione:
e i PG = – 1 ovvero eiPG +1=0
dovuta ad Eulero stesso e che è un po’ una sintesi della matematica giacché mette in relazione tra loro i cinque numeri principali: 0, 1, e, i e Pigreco, i tre principali operatori: " + ", "×" e l’ elevazione a potenza, ed il simbolo "=" dell’eguaglianza.
Conclusioni
Non si ha la pretesa di aver risolto la disputa; per anni si parlerà ancora del numero di Nepero in omaggio alla grande intuizione dello Scozzese o di numero di Eulero in omaggio al grande contributo dato dallo Svizzero alla matematica. Scelga il lettore!

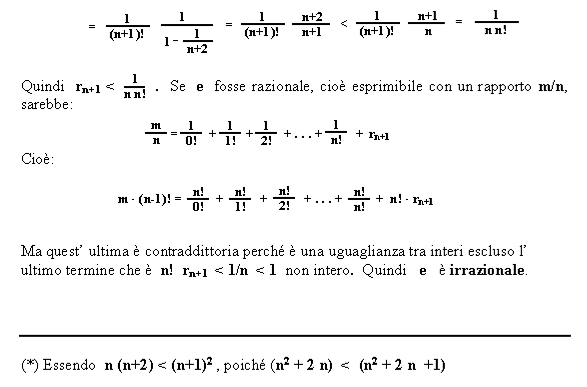
Archimede, sfera e cilindro
 Il problema del rapporto tra volume della sfera e volume del cilindro circoscritto alla sfera è ritornato di attualità da quando nell’esame di stato per la maturità scientifica PNI del 2001 è stato chiesto di "Provare che una sfera è equivalente ai 2/3 del cilindro circoscritto." Chi conosce un po’ di storia della matematica si ricorderà della famosa tomba di Archimede sulla quale lo scienziato siracusano aveva voluto che si scolpisse una sfera e un cilindro.
Il problema del rapporto tra volume della sfera e volume del cilindro circoscritto alla sfera è ritornato di attualità da quando nell’esame di stato per la maturità scientifica PNI del 2001 è stato chiesto di "Provare che una sfera è equivalente ai 2/3 del cilindro circoscritto." Chi conosce un po’ di storia della matematica si ricorderà della famosa tomba di Archimede sulla quale lo scienziato siracusano aveva voluto che si scolpisse una sfera e un cilindro.
Il problema del rapporto tra volume della sfera e volume del cilindro circoscritto alla sfera è ritornato di attualità da quando nell’esame di stato per la maturità scientifica PNI del 2001 è stato chiesto di "Provare che una sfera è equivalente ai 2/3 del cilindro circoscritto." Chi conosce un po’ di storia della matematica si ricorderà della famosa tomba di Archimede sulla quale lo scienziato siracusano aveva voluto che si scolpisse una sfera e un cilindro. 
Quando ero questore in Sicilia mi misi a cercare la sua tomba invasa dalle erbe e dagli sterpi, che i siracusani non conoscevano e anzi negavano che esistesse. Avevo infatti sentito parlare di alcuni versi incisi sulla tomba che spiegavano perché essa fosse sormontata da una sfera e da un cilindro. Fuori da Porta Agrigentina c’è un gran numero di sepolture, e a forza di cercare e di guardare notai finalmente una piccola colona che a pena superava la boscaglia di sterpi, e su di essa erano raffigurati una sfera e un cilindro. Marco Tullio Cicerone Tusculanae Disputationes, V, 23
Archimede ha scritto diversi trattati di geometria, dedicandosi in particolare allo studio dell’area e del volume di alcune forme geometriche. Una delle sue opere più celebri è appunto "Sulla sfera e sul cilindro". L’obiettivo del libro è quello di dimostrare che la sfera è equivalente ai 2/3 del cilindro ad essa circoscritto. Probabilmente, Archimede si era già fatta un’idea che il rapporto doveva essere proprio 2/3. Nella "Misura del cerchio" aveva già dimostrato che la superficie del cerchio è equivalente a quella del triangolo rettangolo avente come cateti la circonferenza rettificata e il raggio (in termini moderni, $C=1/2 *2* pi*r*r= pi*r^2$). Da ciò aveva probabilmente congetturato che il volume della sfera è equivalente a quella del cono avente per cerchio di base la superficie della sfera stessa e per altezza il raggio della sfera ($V_s = 1/3 *S_s*r=4/3 pi*r^3$).
L’intuizione è corretta ma da qui a dimostrarla occorre un notevole apparato di postulati e proposizioni: un intero libro. Vediamo i passaggi principali.
Nel cerchio si inscrive un poligono di 4n lati
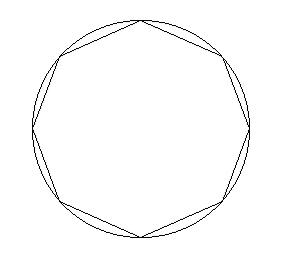
Ruotando la figura, il cerchio forma una sfera, il poligono forma un certo numero di coni e tronchi di cono. Aumentando il numero di lati, il poligono approssima il cerchio, i solidi approssimano la sfera.
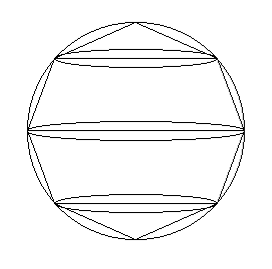
Per sommare coni e tronchi di cono (S1+S2+S3+… ) Archimede ha un’idea brillante. Tutti i solidi che compongono il solido approssimante sono equivalenti a coni aventi tutti la stessa altezza. Più precisamente, i coni hanno per superficie di base la superficie del solido e altezza ($h$ ) la distanza del lato ($l$ ) del poligono dal centro della sfera (Prop. XXIII , Prop. XXIV ) Il problema viene spostato al calcolo della somma delle superfici di $S1, S2, S3, …$ Archimede dimostra che ciascuna superficie Si è equivalente alla superficie di un cerchio il cui raggio è medio proporzionale tra il lato del poligono l e un segmento Li tale che la somma di tutti gli Li corrisponde alla somma delle corde $c1+c2+c3+…$ (Prop XXXII ). In un linguaggio algebrico più moderno e facendo uso del numero PIGRECO
$S1+S2+S3+… = pi*l*(L1+L2+L3+…) = pi*l*(c1+c2+c3+…)
Il problema di sommare le corde $c1+c2+c3+…$ viene risolto dimostrando che $l*(c1+c2+c3+…)=d*A$ dove $d$ è il diametro del cerchio e $A$ è la retta che sottende la metà meno uno dei lati del poligono.
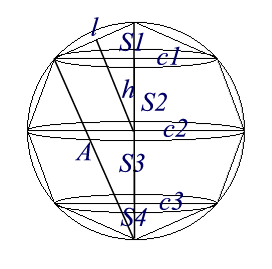
All’aumentare del numero dei lati del poligono, d ed A tendono a coincidere, la superficie del solido approssimante si avvicina sempre di più alla superficie della sfera:
$S1+S2+S3+… = pi*d*A = pi*d*d=4*pi*r^2$
Il volume della sfera è quindi equivalente al volume del cono avente per base la superficie della sfera e altezza il raggio della sfera (Prop. XXV):
$Vs=1/3 *Sc*r = 1/3 *4*pi*r^2*r=4/3 pir^3$
Per questo obiettivo manca ancora il risultato per il quale la superficie della sfera è uguale a quattro cerchi massimi (Prop. XI ). Dimostrato anche questo è facile concludere che la sfera è il doppio del cono avente avente per altezza il diametro della sfera e per base il cerchio massimo della sfera (Prop. XXVI ) e infine che la sfera è equivalente ai 2/3 del cilindro ad essa circoscritto. Lo storico C. Boyer ricostruisce una dimostrazione più immediata del teorema ricorrendo a una relaione di equilibrio scoperta dallo stesso Archimede.
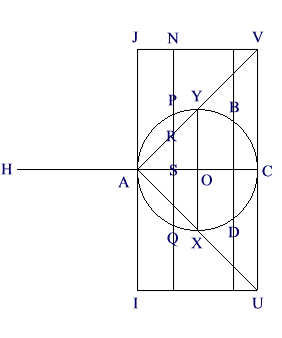 AQDCBP è la sezione trasversale di una sfera di centro O e diametro AC. AUV è la sezione di un cono circolare retto con asse AC, diametro di base UV (doppio del diametro XY della sfera). IJVU la sezione di un cilindro circolare retto con asse AC e diametro di base UV. Sia AH=AC. Si taglia la figura con un piano perpendicolare ad AC, in un punto S qualsiasi. Questo piano taglia sfera, cono e cilindro in cerchi i cui raggi sono SR (cono), SP (sfera), SN (cilindro). Si indicano con A1, A2, A3 le aree di questi cerchi. Archimede dimostra che A1 e A2, posti con i loro centri in H, si equilibrano esattamente con A3, lasciato dov’è, con fulcro in A. Indicati con V1, V2, V3 i volumi della sfera, del cono e del cilindro, si ha che V1+V2=1/2 V3: infatti, tutte le parti di V1 e V3 sono fisse in H, il centro di equilibrio del cilindro è posto in O, AO=1/2 AH. Inoltre poiché è noto che V2=1/3 V3 (il volume del cono è 1/3 del volume del cilindro con stessa base e stessa altezza), V1=1/6 V3. Tenendo conto che il diametro di base del cilindro nel disegno è il doppio del diametro di base del cilindro circoscritto alla sfera, la superficie di base del primo è il quadruplo del secondo. Quindi V1=4/6 V3 = 2/3 V3.
AQDCBP è la sezione trasversale di una sfera di centro O e diametro AC. AUV è la sezione di un cono circolare retto con asse AC, diametro di base UV (doppio del diametro XY della sfera). IJVU la sezione di un cilindro circolare retto con asse AC e diametro di base UV. Sia AH=AC. Si taglia la figura con un piano perpendicolare ad AC, in un punto S qualsiasi. Questo piano taglia sfera, cono e cilindro in cerchi i cui raggi sono SR (cono), SP (sfera), SN (cilindro). Si indicano con A1, A2, A3 le aree di questi cerchi. Archimede dimostra che A1 e A2, posti con i loro centri in H, si equilibrano esattamente con A3, lasciato dov’è, con fulcro in A. Indicati con V1, V2, V3 i volumi della sfera, del cono e del cilindro, si ha che V1+V2=1/2 V3: infatti, tutte le parti di V1 e V3 sono fisse in H, il centro di equilibrio del cilindro è posto in O, AO=1/2 AH. Inoltre poiché è noto che V2=1/3 V3 (il volume del cono è 1/3 del volume del cilindro con stessa base e stessa altezza), V1=1/6 V3. Tenendo conto che il diametro di base del cilindro nel disegno è il doppio del diametro di base del cilindro circoscritto alla sfera, la superficie di base del primo è il quadruplo del secondo. Quindi V1=4/6 V3 = 2/3 V3.
Kline M., Storia del pensiero matematico, Einaudi, Torino, 1992, vol. I, pp. 126-127.
C. B. Boyer, Storia della matematica, Mondadori, Milano,1980, pp. 162-163.
P. D. Napolitani, Archimede, Le scienze (2001), collana "I grandi della scienza", pp. 36-39
http://www.mcs.drexel.edu/%7Ecrorres/Archimedes/contents.html
http://www.thewalters.org/archimedes/frame.html
http://www.maurolico.unipi.it/edizioni/archimed/sphaera/spha-001.htm
http://www2.unife.it/tesi/A.Montanari/Archimed.htm
http://www-groups.dcs.st-and.ac.uk/~history/References/Archimedes.html
Primi elementi di trigonometria
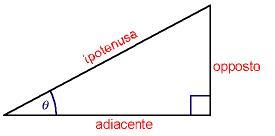
Le relazioni trigonometriche fondamentali sono definite come rapporto di 2 lati di un triangolo rettangolo
di q .
Dove q si riferisce all' angolo acuto del triangolo, il cui lato opposto è 6 e il lato adiacente 4.5. Nota che l'ipotenusa è sempre il lato opposto all'angolo retto ed è sempre il lato più lungo e nel nostro caso vale 7.5.
Che fare se sono date le lunghezze dei lati di un triangolo rettangolo e si vogliono trovare le misure dei suoi angoli acuti? Basta usare le funzioni trigonometriche inverse : asin , acos , e atan .
Sezioni coniche
>
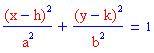
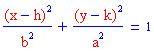
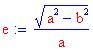
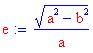
Parabola
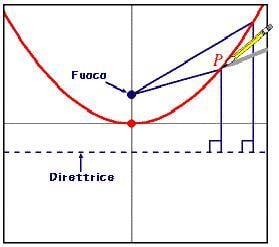
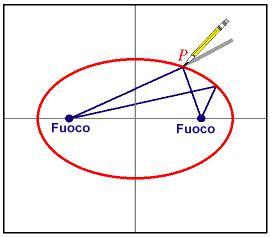
Una parabola è l'insieme dei punti del piano equidistanti da un punto fisso, detto fuoco , e da una retta, detta direttrice .
In altre parole, la distanza dalla punta della matita, P, al fuoco è uguale alla distanza dello stesso punto dalla direttrice, come viene mostrato nel disegno.
Qui sotto è stato disegnato il grafico di una parabola definita da un fuoco e da una direttrice. Prova a cambiare la posizione del fuoco e della direttrice oppure clicca sul grafico seguente.
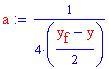
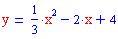

Una parabola è l'insieme dei punti del piano equidistanti da un punto fisso, detto fuoco , e da una retta, detta direttrice .
In altre parole, la distanza dalla punta della matita, P, al fuoco è uguale alla distanza dello stesso punto dalla direttrice, come viene mostrato nel disegno.
Qui sotto è stato disegnato il grafico di una parabola definita da un fuoco e da una direttrice. Prova a cambiare la posizione del fuoco e della direttrice oppure clicca sul grafico seguente.
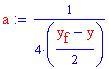
"118" height="39">
Iperbole
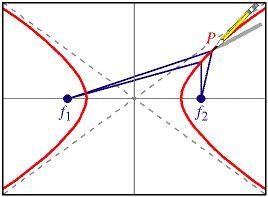
L'iperbole è l'insieme dei punti del piano tali che la differenza delle distanze da due punti fissi, detti fuochi, è costante.
In altre parole, la distanza del punto P sull'iperbole da f 1 meno la distanza di P da f 2 è una costante, s.
Poichè in un triangolo un lato è maggiore della differenza degli altri due la costante s (differenza tra Pf 1 e Pf 2 ) deve essere maggiore di zero, ma minore della distanza tra i due fuochi.
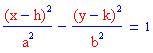
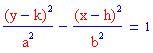
Qui sotto sono stati disegnati i grafici di un'iperbole orizzontale e di una verticale. Puoi provare a cambiare le costanti a e b oppure clicca sui grafici seguenti!
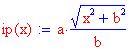
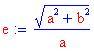
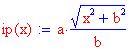
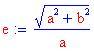
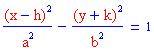
Avrai ormai familiarità con i metodi visti precedentemente per risolvere un problema come questo. Se non ci riesci clicca qui!
Poligoni regolari
Un poligono regolare è equilatero ed equiangolo. Quando i vertici di un poligono giacciono su un cerchio si dice che il poligono è inscritto, quando invece ogni lato del poligono è tangente alla circonferenza si dice che esso è circoscritto.

Per un poligono inscritto, il raggio del cerchio corrisponde alla lunghezza del segmento che va dal centro del poligono ad uno dei suoi vertici.
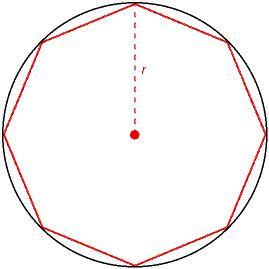
Per un poligono circoscritto il raggio del cerchio corrisponde alla distanza dal centro dei suoi lati
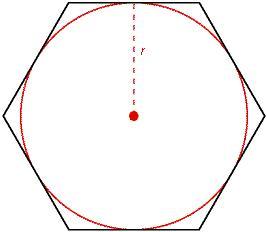
Confronta l'area di un cerchio con l'area del poligono di n-lati inscritto in esso e del poligono di n-lati circoscritto.
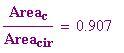
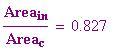
In questa sezione faremo vedere come, per disegnare un poligono regolare di N lati si possono sfruttare le radici complesse dell'unità ,che si distribuiscono simmetricamente rispetto all'origine degli assi cartesiani.
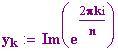
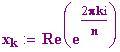

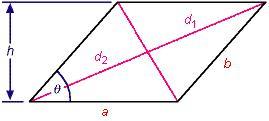
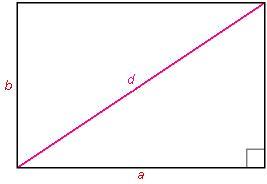
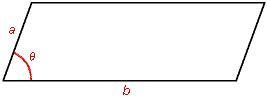
Parallelogramma


Triangolo
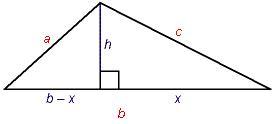
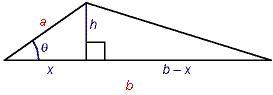
Il triangolo è una figura delimitata da tre segmenti che congiungono tre punti non allineati e che soddisfano la seguente proprietà: ognuno di essi è minore della somma degli altri due ed è maggiore della loro differenza. I segmenti sono chiamati lati del triangolo, i punti sono i vertici del triangolo. Rispetto agli angoli si possono definire tre tipi di triangoli: il triangolo acutangolo che ha tutti gli angoli minori di 90°, il triangolo ottusangolo che ha un angolo maggiore di 90°, il triangolo rettangolo che ha un angolo uguale a 90°.Il triangolo equilatero, che è anche equiangolo, è un particolare triangolo acutangolo.
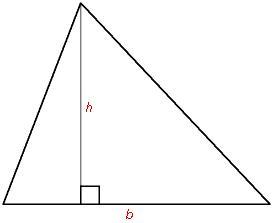
Se stai lavorando con un triangolo rettangolo, basta che tu conosca la lunghezza di due lati (o di un lato e di un angolo acuto) per trovare area e perimetro.
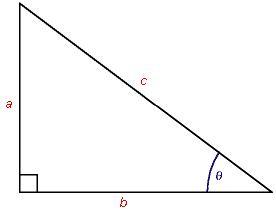
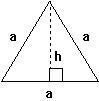
Tutti i triangoli equilateri sono simili (hanno la stessa forma ma no necessariamente le stesse misure per quanto riguarda i lati). Se sai la lunghezza di un lato del triangolo puoi calcolare area e perimetro.
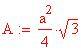
Esercizi sul trapezio
Un trapezio è un quadrilatero con due lati opposti paralleli che si chiamano basi e due lati obliqui. I lati obliqui di un trapezio isoscele hanno la medesima lunghezza.
Basi :
Prisma
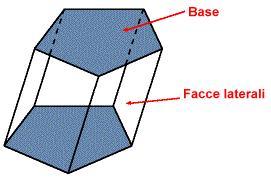
Il prisma è un solido costituito da due poligoni di n-lati congruenti, giacenti su piani paralleli (chiamati basi) e da n facce (chiamate facce laterali).
Le facce laterali di un prisma obliquo sono parallelogrammi, mentre le facce laterali di un prisma retto sono dei rettangoli.
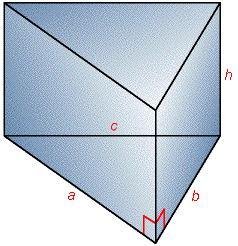
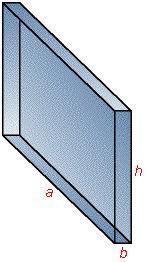
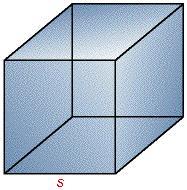
L'area della superficie di tutti i prismi è data dalla somma dell'area delle facce laterali più due volte l'area di base; il volume è uguale all'area di base per l'altezza.
Circonferenza tangenti secanti
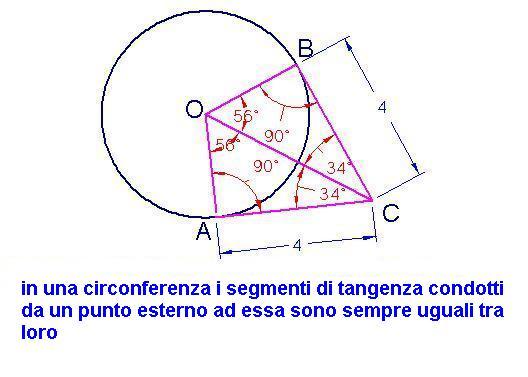
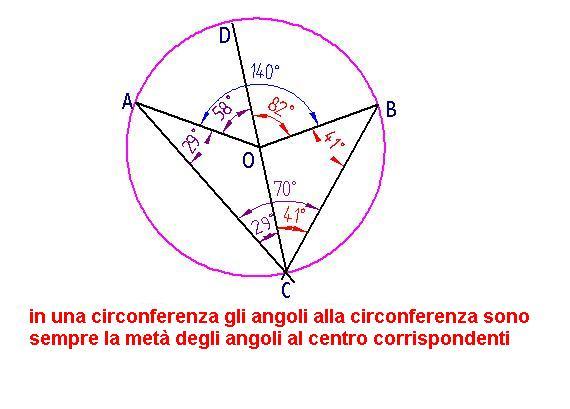
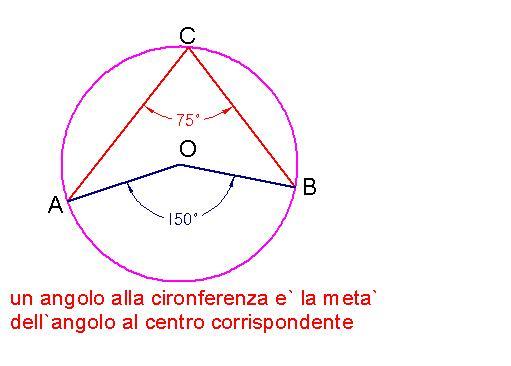
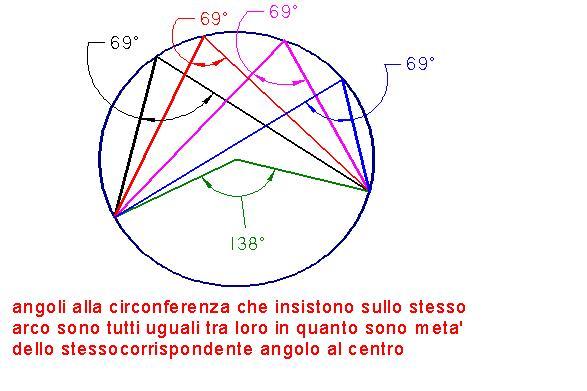
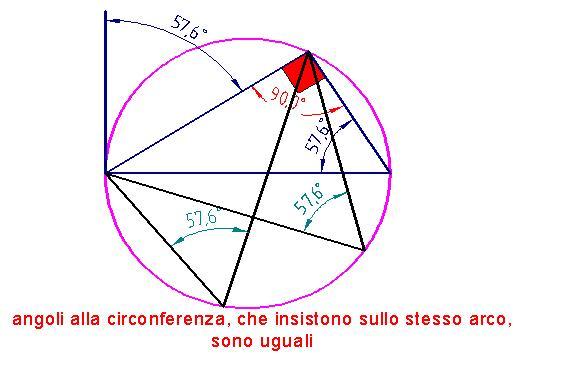
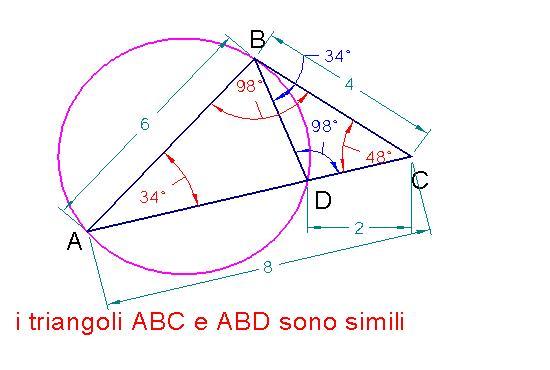
resta così verificato il famoso teorema della tangente e della secante : se da un punto esterno di una circonferenza si conduce una tangente ed una secante il segmento di tangenza è medio proporzionale tra l'intera secante e la sua parte esterna
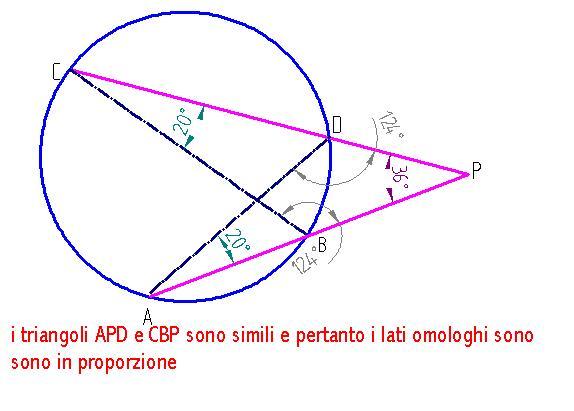
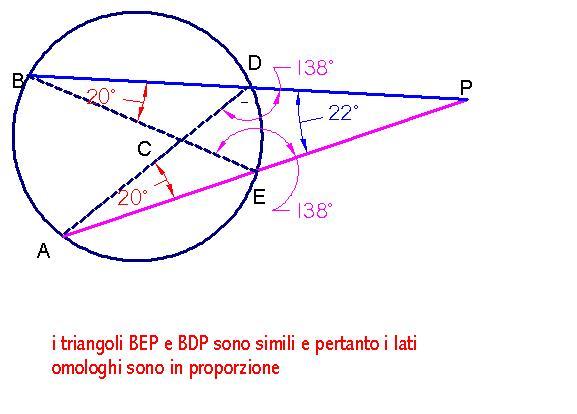
resta così verificato il famoso teorema delle due secanti: se da un punto esterno di una circonferenza si conducono due secanti i segmenti intercettati dalle intersezioni della circonferenza con le secanti sono proporzionali e più precisamente i segmenti intercettati su una secante possono essere considerati i medi e i segmenti intercettati sull'altra secante possono essere considerati gli estremi di una proporzione o anche
Rc circuiti
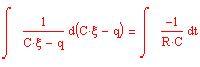
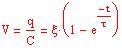
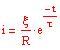
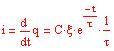
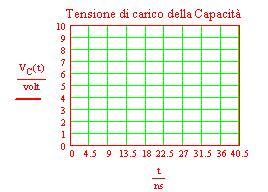
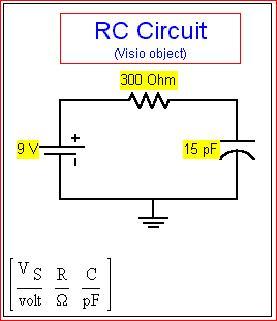
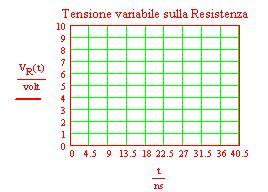
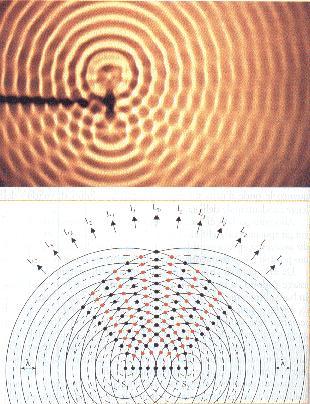
Esperimento di Young
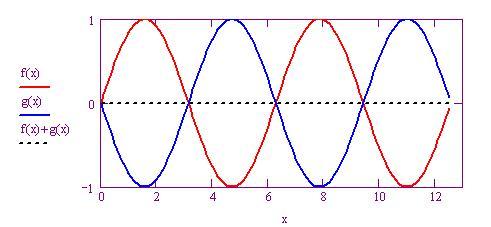
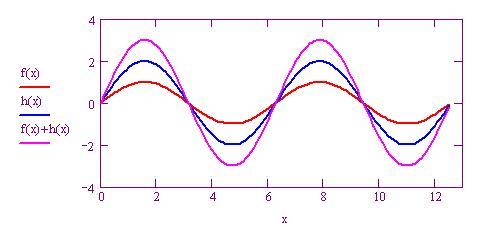
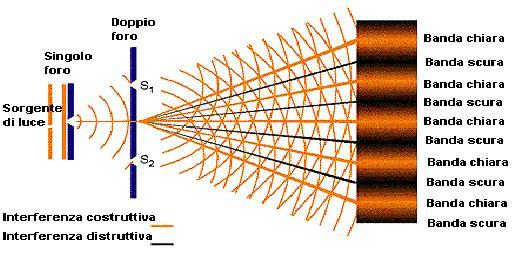
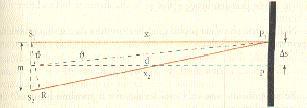
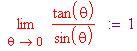
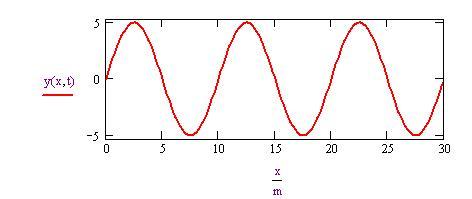
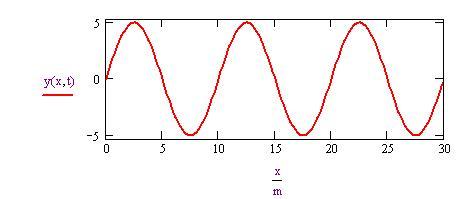
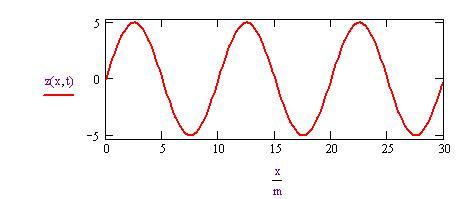
Equazione di un’onda sinusoidale
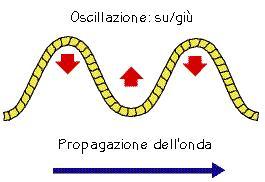
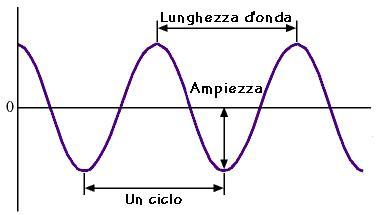
Costruiamo un'onda sinusoidale con i seguenti parametri:
Gli altri parametri possono essere calcolati usando l'equazione dell'onda: