Autore: Francesca Ricci

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I numeri quantici

Appunti: I semiconduttori

L’effetto fotoelettrico e l’ipotesi di Einstein

L’effetto fotoelettrico

L’effetto fotoelettrico, come già sappiamo, consiste nell’emissione di elettroni da parte di una superficie metallica, o da un conduttore, quando essa è colpita da radiazione elettromagnetica.

Ciò avviene perché l’onda elettromagnetica trasporta energia, e quando colpisce la superficie metallica, cede la sua energia alle particelle presenti in essa; se gli elettroni ricevono una quantità di energia maggiore del lavoro di estrazione (cioè il minimo lavoro necessario per far uscire un elettrone da un metallo), allora essi possono liberarsi dalla superficie metallica.

L’effetto fotoelettrico può anche essere utilizzato per spiegare il concetto di quanto del campo elettromagnetico proposto da Planck.

Esperimento del tubo a vuoto

Gli esperimenti furono condotti dal fisico tedesco Lenard, il quale scoprì che la corrente di elettroni emessa da un metallo colpito da radiazione elettromagnetica è direttamente proporzionale all’irradiamento del metallo.

L’esperimento è stato condotto prendendo un tubo a vuoto, all’interno del quale si trovano due lastre metalliche, di cui una funge da anodo, e l’altra da catodo, il tutto inserito in serie in un circuito dotato di amperometro.

La radiazione elettromagnetica, in questo caso una radiazione ultravioletta, colpisce il catodo, che emette una corrente di elettroni che poi colpiscono l’anodo.

effetto-fotoelettrico

Notiamo che l’emissione di elettroni da parte del catodo, e la successiva ricezione da parte dell’anodo dipende anche dalla differenza di potenziale presente tra di essi; in particolare, se l’anodo possiede una differenza di potenziale molto negativa rispetto al catodo, la corrente uscente da quest’ultimo tende a perdere energia cinetica, fino ad arrestarsi.

Di conseguenza, supponendo che il catodo abbia potenziale nullo, in prossimità di esso l’elettrone possiede solo energia cinetica, mentre quando giunge all’anodo, esso possiede solo energia potenziale.

Per la conservazione dell’energia, quindi, si ha la seguente relazione:

$ K_(CATODO) = e * ∆V_(ANODO)$

L’energia cinetica iniziale dell’elettrone è anche la sua energia cinetica massima, in quanto mano a mano che l’elettrone si avvicina all’anodo, la sua energia cinetica diminuisce sempre di più.

Il potenziale dell’anodo viene anche definito potenziale di arresto, perché con questo valore di potenziale, qualsiasi elettrone emesso dal catodo giunge all’anodo con velocità nulla.

Energia cinetica e frequenza della radiazione

Dagli studi più recenti, si evince che l’energia cinetica massima che possiedono gli elettroni emessi non dipendono dall’irradiamento della radiazione elettromagnetica, ma dalla frequenza con cui essa colpisce la lastra metallica.

Queste previsioni contraddicono le leggi di Maxwell, il quale riteneva che l’energia cinetica degli elettroni dipendesse proprio dall’energia da essi posseduta, e quindi dall’irradiamento ricevuto.

Grazie agli studi condotti da Planck, fu possibile per Einstein trovare una spiegazione dell’effetto fotoelettrico che si discosta da quella della fisica classica.

L’ipotesi di Einstein

Einstein propose, infatti, che la trasmissione di energia da parte di una radiazione elettromagnetica avvenisse proprio tramite pacchetti di energia, ai quali fu dato il nome di fotoni.

Ogni fotone trasporta un pacchetto di energia pari a $E = h * f$, dove h è la costante di Planck e f è la frequenza della radiazione elettromagnetica.

Nell’effetto fotoelettrico, ogni fotone interagisce con un singolo elettrone, il quale può liberarsi dalla superficie metallica solo se possiede un’energia maggiore al lavoro di estrazione.

Dato che l’energia dipende dalla frequenza della radiazione, possiamo individuare una frequenza minima che permette agli elettroni di lasciare il metallo:

$ f_(min) = frac(W_e)(h)$

Per mostrare che l’energia cinetica massima posseduta da un elettrone non dipende dall’irradiamento, ipotizziamo che l’elettrone riceva dal fotone con cui interagisce un’energia pari a E = h∙f; l’energia che permette all’elettrone di lasciare il metallo è pari al lavoro di estrazione; di conseguenza, per la conservazione dell’energia, l’energia cinetica che esso possiede all’uscita dal metallo è data da:

$K_(max) = h * f – W_e$

Possiamo quindi osservare che l’energia cinetica dipende solo dalla frequenza della radiazione elettromagnetica e, come era stato osservato sperimentalmente, non dipende dall’irradiamento.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto Compton

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I numeri quantici

Appunti: I semiconduttori

L’effetto Compton

Il fisico statunitense Arthur Compton mise in evidenza che la luce possiede, oltre alle caratteristiche ondulatorie della fisica classica, in determinate condizioni, anche proprietà corpuscolari. Egli, infatti, sosteneva che la luce fosse costituita da particelle dotate di energia.

In particolare, i suoi esperimenti mostrarono che quando un fotone proveniente da una radiazione elettromagnetica colpisce un elettrone della materia, l’urto che ne deriva comporta una perdita di energia del fotone, che in questo modo mette in movimento l’elettrone, come facendolo rimbalzare.

I suoi esperimenti si basavano sull’utilizzo dei raggi X; inviando un fascio monocromatico di raggi X di lunghezza d’onda λi contro un blocco di grafite, egli misurò l’intensità dei raggi in funzione della lunghezza d’onda, ad angoli diversi rispetto alla direzione iniziale.

I risultati mostrarono che, attraversando il blocco di grafite, i fotoni perdevano energia, cosicché la frequenza della radiazione uscente del blocco era assai minore di quella del fascio entrante.

Di conseguenza, la lunghezza d’onda delle onde elettromagnetiche uscenti dalla grafite era maggiore di quella iniziale; tra le radiazioni uscenti, quindi, si registrarono due picchi di lunghezze d’onda diverse: una di esse era uguale a quella iniziale, e dovuta all’oscillazione degli elettroni nella grafite, a causa della radiazione incidente; l’altra, invece, deve essere spiegata con la fisica quantistica, e con le ipotesi di Einstein.

Infatti, Compton ipotizzò che, l’urto tra un fotone e un elettrone, può essere immaginato alla pari dell’urto tra due palline da biliardo: quando il fotone urta l’elettrone, trasferisce ad esso parte della sua energia e quantità di moto, cambiando anche direzione di propagazione. L’elettrone, d’altra parte, viene messo in movimento grazia all’energia cinetica acquisita.

Quando il fotone uscirà dalla grafite, quindi, possederà un’energia minore di quella iniziale, e si propagherà anche con una frequenza minore; di conseguenza, la lunghezza d’onda della radiazione emessa sarà maggiore della precedente.

La differenza tra la lunghezza d’onda del fotone uscente e quella dell’elettrone dopo l’urto si definisce Spostamento Compton.

Grazie anche alla relatività ristretta, è stato possibile ricavare una relazione che fornisce la misura dello Spostamento Compton:

$∆λ = λ’ – λ = frac(h)(m_e * c) * (1 – cos φ )$

dove λ indica la lunghezza d’onda della radiazione iniziale, mentre λ’ la lunghezza d’onda di quella uscente; m indica la massa di un elettrone, mentre φ l’angolo di deviazione del raggio rispetto alla direzione iniziale.

Esercizio

Ipotizziamo di ripetere l’esperimento di Compton, utilizzando un fascio di raggi X diretto su di un blocco di grafite. Supponiamo che la radiazione sia diffusa con un angolo di deviazione di 60° rispetto alla direzione iniziale. Calcolare la variazione di lunghezza d’onda osservata, e la lunghezza d’onda a cui si misurano i massimi nella radiazione diffusa se i raggi iniziali hanno una lunghezza d’onda di $7,09 * 10^(-11) m$.

Per risolvere il problema, avendo tra i dati l’angolo di deviazione della direzione del fotone uscente, possiamo applicare la formula vista precedentemente:

$∆λ = λ’ – λ = frac(h)(m_e * c) * (1 – cos φ )$

Ricordiamo che i valori della costante di Planck, della massa dell’Eleonora e della velocità della luce sono noti, e valgono:

$ h = 6,63 * 10^(-34) J*s$

$m_e = 9,11 * 10^(-31) kg $

$ c = 3,00 * 10^8 m/s$

Sostituendo i valori numerici nella formula precedente otteniamo:

$∆λ = frac(6,63 * 10^(-34))(9,11 * 10^(-31) * 3,00 * 10^8) * (1 – cos 60° ) = 0,12 * 10^(-11) m$

Per risolvere il secondo quesito, poi, consideriamo che la differenza di lunghezze d’onda è data da quella finale meno quella iniziale; di conseguenza, la lunghezza d’onda della radiazione emessa sarà data da:

$λ’ =∆ λ + λ $

Sostituendo i valori numerici otteniamo:

$λ’ =∆ λ + λ = 0,12 * 10^(-11) + 7,09 * 10^(-11) = 7,21 * 10^(-11) m$

L’effetto Compton inverso

L’effetto Compton inverso si ha quando un fotone a bassa energia interagisce con un elettrone ad alta energia; in questo caso, infatti, è l’elettrone a cedere energia al fotone, e non viceversa.

Questo accade, solitamente, nel caso di elettroni ad alta energia emessi dai raggi cosmici (cioè particelle subatomiche provenienti dallo spazio), che vengono in contatto con fotoni a bassa energia provenienti dalla radiazione cosmica di fondo, ovvero la radiazione residua proveniente dal Big Bang e ancora presente nell’universo.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto fotoelettrico e l’ipotesi di Einstein

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I numeri quantici

Appunti: I semiconduttori

L’energia atomica e il modello di Bohr

Grazie a strumentazioni moderne e sofisticate è stato possibile analizzare anche il tipo di energia posseduta dagli atomi.

Gli esperimenti furono condotti dagli scienziati Franck e Hertz utilizzando una strumentazione di questo tipo: in un tubo riempito del gas oggetto di studio, si trovano una sorgente di elettroni (catodo), una griglia di accelerazione e un anodo.

Durante l’esperimento, gli elettroni venivano emessi dal catodo in modo da urtare le particelle di gas; si studia, quindi, l’energia posseduta dalle particelle.

Gli urti, come sappiano possono essere di due tipi: quelli elastici non alterano l’energia delle molecole, mentre quelli anelastici comportano perdita dell’energia degli elettroni, che viene trasferita alle molecole di gas.

Se gli urti sono elastici, gli elettroni emessi, dopo l’urto, sono in grado di raggiungere l’anodo, perché possiedono ancora energia sufficiente. In questi casi, quindi, si registrano alti picchi di corrente.

Se l’urto è anelastico, invece, parte dell’energia dell’elettrone viene ceduta agli atomi di gas, e di conseguenza gli elettroni non possiedono più energia a sufficienza per raggiungere l’anodo. Si registrano, quindi, dei notevoli abbassamenti di corrente.

Durante l’esperimento si verificano di continuo e contemporaneamente urti elastici e urti anelastici, ma le quantità di energia che possono essere scambiate durante un urto sono ben definite.

Anche in questo caso, quindi, lo scambio di energia è quantizzato.

Il modello di Bohr

Riguardo la quantizzazione dell’energia negli atomi, Bohr propose un nuovo modello atomico, fornendo anche precise condizioni per la quantizzazione dell’energia.

Secondo questo modello, gli atomi sono costituiti da un nucleo positivo, attorno al quale gli elettroni si muovono orbitando su delle orbite ben precise. Ciascuna orbita possiede un determinato livello energetico, e ogni orbita possiede un raggio dato da un determinato insieme di valori permessi.

Inoltre, se un elettrone percorre un orbita con un valore energetico permesso, l’elettrone non irraggia.

I raggi delle orbite permesse possono essere ricavati dalla seguente formula:

$2πr_np_n = nh$

dove p indica la quantità di moto dell’elettrone, h è la costante di Planck, mentre n indica il numero dell’orbita che si sta considerando, e viene definito numero quantico principale: per n = 1, ci troviamo sulla prima orbita.

E’ stato possibile dimostrare che l’energia di un elettrone che percorre l’orbita n-esima è inversamente proporzionale al quadrato di n, e dato dalla formula:

$ E(n) = – frac(13,6 eV)(n^2)$

Vediamo, quindi, che l’energia posseduta dall’elettrone dipende esclusivamente dall’orbita in cui si trova: mano a mano che il numero dell’orbita aumenta, l’energia diventa sempre più piccola in modulo, avvicinandosi sempre di più a valori prossimi allo zero.

Elettroni e livelli energetici

Sul modello della teoria di Bohr, quindi, possiamo spiegare anche il passaggio di energia tra un fotone e un atomo di gas quando i due interagiscono tra loro.

Nel caso di un urto anelastico, infatti, il fotone colpisce l’atomo di gas, cedendo ad esso parte della sua energia.

Come conseguenza, l’energia acquisita dall’atomo permette ad un elettrone di passare da un orbita permessa ad un orbita situata ad un livello energetico maggiore; in questa situazione, l’atomo si dice eccitato.

Quando, poi, l’atomo ritorna nel suo stato fondamentale, cioè l’elettrone ritorna nel livello energetico permesso, l’energia viene ceduta con l’emissione di un fotone da parte dell’atomo. L’effetto visibile è quello dell’emissione di luce.

Questo effetto può essere osservato, ad esempio, analizzando lo spettro a righe in emissione di un gas monoatomico attraversato da corrente.

Lo spettro dell’idrogeno

Nel caso dell’idrogeno, ad esempio, abbiamo uno spettro di questo tipo:

spettro-idrogeno — Lo spettro dell’idrogeno.

Le righe che si osservano si trovano a determinate lunghezze d’onda, e possiedono determinate frequenze, date dalla formula seguente, che prende il nome di serie di Balmer:

$f = c * R_H * (frac(1)(m^2) – frac(1)(n^2))$

dove R è una costante, mentre m e n sono due numeri interi.

Il fenomeno dello spettro di emissione può essere spiegato con la teoria di Bohr; quando il gas è attraversato da corrente, infatti, gli urti tra gli elettroni e gli atomi fanno di che questi ultimi passino allo stato eccitato.

Quando, poi, emettono energia sotto forma di fotoni, ogni fotone possiede una determinata frequenza, ottenibile dalla formula precedente, e rappresenta una precisa riga che compare sullo spettro.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto fotoelettrico e l’ipotesi di Einstein

Appunti: L’effetto Compton

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I numeri quantici

Appunti: I semiconduttori

Il principio di indeterminazione di Heisenberg

Il principio di indeterminazione di Heisenberg rappresenta la base della fisica quantistica.

Tale principio afferma che non è possibile conoscere con precisione e contemporaneamente la posizione di un elettrone e la velocità con cui esso si muove.

Sulla base di questo principio, non si può parlare più di traiettoria per il percorso dell’elettrone. Mentre prima si pensava che l’elettrone si muovesse su traiettorie circolari, gli orbitali, ora si parla di un’area in cui si ha probabilità maggiore di trovare l’elettrone.

In particolare, le probabilità di determinare posizione e velocità dell’elettrone possono essere espresse dalla seguente formula:

$∆x * ∆p ≅ h $

dove h indica un valore approssimativo, della grandezza di $10^(-34) Js $.

Come possiamo osservare, la posizione e la quantità di moto sono inversamente proporzionali: se la misura della posizione diventa più precisa, e quindi ∆x diventa più piccolo, il valore della differenza di quantità di moto, e quindi di velocità, diventa più grande, e quindi meno accurato.

La radiazione nella materia

Con le osservazioni fatte riguardo le radiazioni elettromagnetiche, si giunge alla conclusione che la luce, in quanto onda elettromagnetica, presenta una natura sia ondulatoria che corpuscolare.

Ciò che incuriosì alcuni studiosi è la riflessione sulla possibilità che anche la materia presenti un dualismo di questo tipo.

A questi studi si dedico il fisico francese de Broglie, che scopri che ad ogni particella di materia con quantità di moto p corrisponde una lunghezza d’onda pari a:

$ λ = h/p$

Nel caso di oggetti macroscopici, però, le lunghezze d’onda associate sono molto piccole, tanto da poter essere considerate trascurabili. Per questo non sono osservabili gli effetti prodotti da tali radiazioni.

La funzione d’onda

Dal punto di vista di de Broglie, quindi, anche la materia emette onde elettromagnetiche; uno dei principali quesiti che sorse in seguito a tale dichiarazione fu riguardo alla composizione delle onde di materia.

La risposta a questo quesito permette di definire una nuova grandezza, detta ampiezza di probabilità o funzione d’onda. Secondo la fisica quantistica, infatti, non è possibile definire con un’interpretazione classica cosa sia un’onda di materia.

Questa nuova grandezza, che dipende dai parametri spaziale e da quello temporale, permette di definire la probabilità che una particella si trovi un una regione di spazio considerato.

Una particella, quindi, si troverà nella zona in cui la funzione ψ oscilla, mentre dove la funzione è nulla, tale è anche la probabilità di trovarvi qualsiasi particella.

Questa nuova interpretazione dell’onda di materia fornisce anche una prova della validità del principio di indeterminazione di Heisenberg.

Infatti, sappiamo che all’interno di una regione di spazio di lunghezza ∆x dove oscilla la funzione ψ, e dove abbiamo una certa probabilità di trovare la particella, non possiamo determinare di preciso la posizione che essa occupa.

Se considerassimo un’onda che si estende a tutto lo spazio, potremo conoscere la sua quantità di moto, ma in questo caso ∆p sarebbe nullo, e di conseguenza ∆x raggiungerebbe un valore infinito: ciò significa che non potremo sapere dove si trova la particella.

Dualismo onda-corpuscolo

Possiamo concludere affermando che, in generale, una radiazione elettromagnetica ha una natura sia ondulatoria che corpuscolare, in base alle situazioni che si considerano.

Ad esempio, se l’onda elettromagnetica si propaga nello spazio, essa va considerata come un insieme di pacchetti d’onda (ovvero gruppi di oscillazione della funzione ψ) che possiedono ampiezze di probabilità di tutte le particelle del sistema.

Nel caso in cui, invece, l’onda elettromagnetica interagisse con qualche dispositivo, essa può essere considerata sia come onda che come corpuscolo, in base al tipo di misurazione che viene fatta su di essa.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto fotoelettrico e l’ipotesi di Einstein

Appunti: L’effetto Compton

Appunti: I numeri quantici

Appunti: I semiconduttori

I numeri quantici

Molto spesso, un atomo viene paragonato ad Sistema Solare, in quanto il nucleo può essere rappresentato dal Sole, e gli elettroni che gli orbitano attorno dai pianeti, che seguono traiettorie ellittiche.

Nelle teorie atomiche precedenti, però, le orbite percorse dagli elettroni sono sempre state considerate circolari; tuttavia, fu dimostrato da Sommerfeld che ad un certo numero principale n possono corrispondere n orbite ellittiche che hanno il semiasse maggiore uguale al raggio dell’orbita circolare prevista da Bohr; il semiasse minore, invece, dipende da un numero naturale l, che può variare da 0 a (n-1), e vale:

$ a_m = frac(l + 1)(n) * a_M$

Si può dimostrare che anche il momento angolare di un elettrone che percorre un’orbita ellittica è quantizzato, in quanto esso è un multiplo di una grandezza definita:

$ L = (l + 1) * h$

Il momento magnetico di un elettrone

Anche nel caso degli elettroni si può parlare di momento magnetico; infatti, poiché un elettrone si muove lungo un percorso chiuso, possiamo paragonare il suo moto ad una spira percorsa da corrente.

All’interno di un campo magnetico esterno, una spira percorsa da corrente tende a ruotare (come farebbe un ago magnetico) finché il suo vettore superficie non è parallelo al vettore campo magnetico.

Ricordiamo la definizione di momento torcente come prodotto vettoriale del momento magnetico per il vettore campo magnetico:

$ vec M = vec μ_m × vec B = i vec A × vec B$

il momento magnetico si può esprimere come prodotto dell’intensità di corrente per l’area racchiusa dal percorso della corrente.

Nel caso di una carica elettrica, l’intensità di corrente si può ottenere come rapporto della carica (quella dell’elettrone) per l’intervallo di tempo, in questo caso quello impiegato per compiere un giro completo, ipotizzando l’orbita circolare. Si ha quindi:

$μ_m = i * A = – frac(ev)(2πr) * πr^2$

Si può inoltre trovare una relazione tra il momento magnetico dell’elettrone e il suo momento angolare; si dimostra, quindi, che il vettore momento magnetico è dato da:

$ vecμ_m = – 1/2 * frac(e)(m_e) * vec L $

Dalla teoria della quantizzazione dell’energia per gli atomi, si evince che anche in questo caso, sono possibili solo determinati valori del momento magnetico e di quello angolare, così come solo alcune delle loro direzioni sono permesse.

Si dimostra che gli stati permessi solo quelli in cui le componenti di L sono parallele al vettore campo magnetico. Tali componenti dipendono da un numero intero m, detto numero quantico magnetico, che assume valori compresi tra -l e +l.

I numeri quantici

I numeri interi che comparivano nelle formule viste precedentemente, e che definiscono le caratteristiche degli orbitali, hanno nomi specifici, e ciascuno di essi determina caratteristiche specifiche.

Il numero n si definisce numero quantico principale, che determina le grandezze dell’orbitale (e il guscio) su cui si trova l’elettrone, ed in particolare la distanza media degli elettroni dal nucleo. Questo numero può assumere tutti i valori interi a partire da n = 1.

Il numero l si definisce numero quantico angolare, o azimutale, e definisce il momento magnetico orbitale; in base al suo valore, che varia da 0 a (n-1), gli orbitali vengono classificati nei tipi s, p, d, f; tale numero indica anche il numero dei sottogusci di ciascun livello n.

Il numero m, infine, si definisce numero quantico magnetico; esso determina l’energia dovuta all’allineamento del momento orbitale con un campo magnetico esterno.

Il quarto numero quantico viene definito numero quantico di spin, che quantizza il momento angolare dell’elettrone; questo numero può assumere solo i valori di 1/2 e -1/2, che determina il verso di rotazione dell’elettrone su se stesso.

La scoperta del quarto numero quantico deriva dal principio di esclusione di Pauli; questo afferma che due elettroni dello stesso atomo non possono avere numeri quantici uguali.

Dato che un guscio di numero principale n può contenere fino a n^2 elettroni, deve necessariamente esistere un altro numero quantico che possa assumere solo due valori.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto fotoelettrico e l’ipotesi di Einstein

Appunti: L’effetto Compton

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I semiconduttori

Legami chimici e bande di energia

I legami chimici

Gli atomi che compongono la materia sono legati tra loro da forze attrattive tra le particelle elementari, che costituiscono il legame chimico.

Ogni legame può essere rotto, e per farlo occorre vincere queste orze attrattive; occorre fornire, quindi, un’energia sufficiente a vincere tali forze. Questa energia prende il nome di energia di legame, ed è pari alla differenza tra l’energia complessiva degli atomi isolati e a quella complessiva dell’aggregato molecolare.

Tra i legami chimici più diffusi troviamo il legame covalente, che prevede la condivisione da parte di due atomi di una o sue coppie di elettroni.

Dal punto di vista della fisica quantistica, il legame covalente può essere descritto considerando la funzione d’onda ψ.

Nel caso più semplice, quello dell’idrogeno, la molecola di idrogeno H2 è composta da due atomi, ciascuno dei quali mette in condivisione un elettrone.

Legami chimici e funzione d’onda

Se osserviamo il fenomeno dal punto di vista della fisica quantistica, possiamo considerare la probabilità che si ha di trovare un elettrone in una determinata regione di spazio.

Sapendo che la probabilità di osservare la particella in quella determinata regione è proporzionale al quadrato di ψ, e considerando uguali le probabilità di trovare l’elettrone in una regione ∆V per entrambi gli atomi di H, possiamo stabilite che l’ampiezza di probabilità può essere di due tipi: nel caso in cui la funzione ψ sia pari, e nel caso in cui ψ dia dispari.

Il primo caso si ha quando ψ in due punti simmetrici ha lo stesso modulo e lo stesso segno, mentre nel secondo caso la funzione assume uguale modulo, ma segno opposto.

Dallo studio dei grafici delle funzioni ψ pari e dispari, emerge che nel caso della funzione dispari, l’elettrone ha una bassa probabilità di trovarsi nella regione di spazio centrale della molecola, compresa tra i due atomi; nel secondo caso, invece, per funzioni pari, l’elettrone ha alte probabilità di trovarsi in tale regione, in quanto sono presenti forze attrattive intense dovute alla presenza delle cariche positive.

La funzione pari, quindi, che è quella a più bassa energia per l’elettrone, mostra che la probabilità di trovare l’elettrone nella regione di spazio centrale è molto elevata; tale funzione, quindi, è quella che descrive un elettrone maggiormente attratto, e più coinvolto nel legame:

legami-chimici

Possiamo osservare che quando gli atomi sono nello stato fondamentale, isolati, gli elettroni sono descritti da una funzione d’onda che circonda il nucleo atomico.

Quando, però, gli atomi vengono avvicinati, si ha come uno sdoppiamento dei livelli di energia; si sovrappongono, infatti, due stati energetici differenti, uno a energia minore dato dalla funzione d’onda pari, e l’altro a energia maggiore dato dalla funzione d’onda dispari.

Caso del reticolo cristallino

Le considerazioni precedenti possono essere estese al caso di più atomi legati tra loro, come avviene per esempio in un reticolo cristallino.

Finché gli atomi (dello stesso tipo) si trovano lontani e separati, ciascuno di essi possiede lo stesso livello energetico; quando gli atomi vendono avvicinati, ogni livello energetico si scinde in un certo numero di livelli energetici differenti, se pur molto simili; il numero di livelli energetici che si forma è dato dal numero di atomi che vengono raggruppati.

Poiché un cristallo è formato da un numero grandissimo di atomi, i livelli energetici che si formano saranno talmente vicini tra loro da formare come una “banda” energetica continua.

In base alle bande energetiche possedute dai vari elementi, possiamo classificarli in conduttori o isolanti.

Infatti, negli elementi che possiedono delle bande energetiche piene non vi sono elettroni liberi di muoversi, in quanto tutti i livelli energetici sono occupati.

Nel caso in cui, invece, vi siano bande energetiche parzialmente piene, è più facile che gli elettroni passino a livelli energetici superiori, creando così una corrente elettrica.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto fotoelettrico e l’ipotesi di Einstein

Appunti: L’effetto Compton

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I numeri quantici

Appunti: I semiconduttori

I semiconduttori

I semiconduttori sono dei materiali solidi che presentano caratteristiche intermedie tra quelle dei conduttori e quelle degli isolanti.

Le caratteristiche dei semiconduttori dal punto di vista della fisica quantistica, mostrano una particolarità per quanto riguarda le bande di energia degli elementi.

Si nota che, nel caso di qualunque semiconduttore, la formazione di una banda riempita da elettroni (banda di valenza), e una banda vuota (banda di conduzione).

Il drogaggio dei semiconduttori

In molti casi è possibile aumentare la conducibilità elettrica di un semiconduttore introducendo in esso delle piccole impurezze atomiche. In questo caso si dice che il semiconduttore è drogato.

Ad esempio, consideriamo un semiconduttore di silicio; ogni atomo di silicio forma quattro legami covalenti con quattro atomi di silicio, formando così una struttura tetraedrica.

Il drogaggio di tale conduttore consiste nel sostituire un atomo di silicio presente nella struttura cristallina con un atomo di un altro elemento; quest’ultimo deve poter formare un numero di legami con gli altri atomi maggiore o minore di quelli che forma il silicio.

Drogaggio di tipo “n”

Ad esempio, si può sostituire l’atomo di silicio con un atomo di fosforo, che ha cinque elettroni nel guscio più esterno; quindi questo può formare cinque legami con gli atomi circostanti, un legame in più rispetto al silicio. Quindi, l’atomo di fosforo lega quattro atomi di silicio, mentre un elettrone rimane libero. Gli elettroni liberi in eccesso possono muoversi sulla superficie del reticolo, così da migliorare il passaggio di corrente.

Osserviamo cosa accade alle bande di energia; come abbiamo detto, nel caso di un conduttore normale si ha una banda completamente piena e una completamente vuota.

Drogando il silicio con atomi di arsenico, gli elettroni in eccesso andranno ad occupare parte della banda di conduzione; potendosi muovere liberamente all’interno di essa, favoriscono il passaggio della corrente. Un drogaggio di questo tipo viene detto drogaggio di tipo “n” ( n come negativo ).

Drogaggio di tipo “p”

Consideriamo, ora, il drogaggio del semiconduttore di silicio con un atomo che può legare un numero minore di atomi rispetto al silicio.

Ad esempio, si può sostituire un atomo di silicio con uno di boro, che possiede tre elettroni sul guscio esterno, e quindi può formare solo tre legami.

In questo caso, l’atomo di boro può legarsi solo con tre dei quattro atomi circostanti, cosicché si formano delle vacanze di elettroni, cioè delle buche. L’elettrone proveniente dall’atomo di silicio non legato, infatti, è libero di muoversi.

drogaggio-di-tipo-p — Drogaggio di tipo “p”.

Questa volta, però, si hanno delle buche anche nella banda di valenza.

All’interno del reticolo le buche possono essere considerate come delle cariche positive; gli elettroni liberi possono muoversi nel reticolo “saltando” dentro le buche, e quando lo fanno lasciano dietro di loro altre buche vuote. Questi movimenti degli elettroni rappresentano, quindi, il passaggio di corrente.

Un drogaggio di questo tipo viene definito di tipo “p”(p come positivo).

Notiamo le buche possono essere considerate come particelle positive in quanto il loro moto avviene nella stessa direzione del campo elettrico.

Infatti, gli elettroni tendono a muoversi in verso opposto al campo elettrico, ma quando lo fanno provocano lo spostamento di una lacuna nel senso opposto.

A partire dal valore delle velocità di deriva delle lacune e degli elettroni, si può dimostrare che esiste una relazione tra la resistività del semiconduttore e il numero degli elettroni di conduzione (n) e il numero delle lacune (p), e che essa è data dalla seguente formula:

$ 1/ρ = e * (n * frac(v_n)(E) + p * frac(v_p)(E))$

dove e indica la carica dell’elettrone, mentre E il campo elettrico applicato al semiconduttore.

In particolare, i rapporti tra le velocità di deriva i il modulo del campo elettrico costituiscono delle grandezze definite mobilità.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto fotoelettrico e l’ipotesi di Einstein

Appunti: L’effetto Compton

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I numeri quantici

Dispositivi a semiconduttori

Il diodo a semiconduttore

Un dispositivo di questo tipo è formato da due parti, delle quali una è un semiconduttore di tipo “n”, mentre l’altra è di tipo “p”.

A causa dell’agitazione termica, il movimento delle lacune e degli elettroni fa si che si crei una corrente di elettroni e di lacune che si muovono in sensi opposti.

Quando un elettrone di conduzione si sposta dal semiconduttore di tipo “p” per andare in quello di tipo “n”, occupando una lacuna, si ha nello stesso tempo lo spostamento di una lacuna dal conduttore di tipo “n” a quello di tipo “p”. Questo tipo di movimento è detto ricombinazione.

Questo continuo movimento fa si che tra le due zone si crei una parte definita “di svuotamento”, in cui non vi sono portatori di cariche; inoltre, lo spostamento delle lacune e degli elettroni in versi opposto crea una divisione di cariche all’interno del dispositivo, il che genera a sua volta un campo elettrico diretto dal semiconduttore di tipo “n” a quello di tipo “p”.

Schema diodo a semiconduttore

La separazione delle cariche, e la formazione del campo elettrico inoltre, generano una differenza di potenziale, che può essere sfruttata all’interno di un circuito.

Tuttavia, il diodo a semiconduttore funzione in maniera particolare se inserito in un circuito, in quanto permette il passaggio di corrente solo in un verso, e non nel verso opposto.

Polarizzazione diretta e inversa

In un diodo a semiconduttore si può applicare una polarizzazione diretta o inversa.

Nel caso in cui si collega alla regione “n” il polo positivo di un generatore, e alla regione “p” quello negativo, si ha una polarizzazione inversa.

In questo caso, tra le due zone può passare solo una corrente molto debole, perché la presenza del campo elettrico esterno fa si che vengano estratte delle lacune dalla regione “p” e elettroni dalla regione “n”.

Quando invece si collegano le due zone in modo opposto, cioè alla regione “n” si collega il polo negativo, mentre alla regione “p” quello positivo, si ha una polarizzazione diretta, con conseguente circolazione di corrente.

Il transistor

Il transistore è un dispositivo che permette di controllare l’intensità di corrente elettrica.

Esistono due tipi di transistori, che si differenziano per il modo in cui è suddivisa la regione centrale di cui è costituito il cristallo.

Tale regione, infatti, è costituita da tre zone, in cui possono alternarsi i semiconduttori di tipo “n” e “p”: in un caso, un semiconduttore di tipo “p” è inserito tra due di tipo “n”, mentre nell’altro un semiconduttore di tipo “n” è inserito tra due di tipo “p”.

Questo tipo di dispositivo viene utilizzato inserito in un circuito come quello in figura, in cui si utilizzano due generatori di tensione:

transistor

La parte centrale, detta base, deve avere un potenziale elettrico intermedio tra quello delle due regioni laterali, dette emettitore e collettore.

Se il potenziale della base fosse maggiore o minore di quello delle zone limitrofe, non circolerebbe corrente; infatti, gli elettroni dell’emettitore passerebbero alla base (oltrepassando la giuntura che è polarizzata direttamente), ma qui si fermerebbero, ricombinandosi con le lacune (e non oltrepassano la giunzione tra base e collettore, che è polarizzata inversamente).

Con una giusta differenza di potenziale tra le zone, invece, gli elettroni giunti nell’emettitore passerebbero nella base che, essendo costituita da una regione molto sottile, consente ad una frazione degli elettroni di passare al collettore; da qui, poi, gli elettroni possono fluire nel circuito esterno.

Abbiamo detto inizialmente che il transistore è un dispositivo che permette di controllare l’intensità di corrente; in effetti, è possibile modificare l’intensità di corrente variando la tensione tra la base e l’emettitore; quando il potenziale viene abbassato, la corrente tra base ed emettitore diventa più piccola; aumentando il potenziale, invece, anche la corrente aumenta.

Come nel caso del diodo a semiconduttore, anche per il transistore vi è un caso particolare in cui non fluisce corrente, e cioè quando anche la giunzione tra base ed emettitore è polarizzata inversamente; in questo caso si dice che il transistore si trova in regime di interdizione.

In questo stato, il dispositivo può fungere da interruttore, permettendo o meno il passaggio della corrente in base al valore della tensione tra base ed emettitore.

Potrebbero Interessarti

VideoLezioni: La meccanica quantistica

Appunti: La legge di Planck

Appunti: L’effetto fotoelettrico e l’ipotesi di Einstein

Appunti: L’effetto Compton

Appunti: Il principio di indeterminazione di Heisenberg

Appunti: I numeri quantici

Appunti: I semiconduttori

La velocità della luce

Come abbiamo già visto, le teorie che si presentarono nel corso degli anni sulla natura della luce furono diverse, e spesso contraddittorie tra loro. Alcune di esse non riguardano soltanto la natura della luce, ma anche la sua velocità e il modo in cui essa si propaga.

In questo caso, infatti, troviamo l’opposizione di due teorie, una formulata nell’ambito della meccanica, e l’altra nell’ambito dell’elettromagnetismo.

Le trasformazioni di Galileo

Nel primo caso, il sostenitore della teoria è Galileo Galilei, secondo il quale la velocità della luce dipende dal sistema di riferimento che stiamo considerando. Infatti, anche se in sistemi di riferimento diversi valgono le stesse leggi della meccanica, è possibile che il moto di un corpo possa essere descritto da leggi diverse nei due sistemi di riferimento.

Consideriamo due sistemi di riferimento S ed S’, quest’ultimo in moto rispetto ad S, entrambi sistemi di riferimento inerziali. Indichiamo con t il tempo misurato in S, con t’ il tempo misurato in S’. Dato che S’ si muove in S, supponiamo a velocità costante, indichiamo con V tale velocità.

Le trasformazioni di Galileo permettono di passare dalle grandezze misurate in S’ a quelle che si misurano in S, e viceversa:

${ (vec s = vec s’ + vec V * t’) , (t = t’ ):} , { (vec s’ = vec s – vec V * t’) , (t’ = t):}$

Come possiamo vedere, le equazioni sono equazioni vettoriali, e i vettori s e s’ indicano la posizione di un punto P rispetto alle origini dei due sistemi di riferimento.

Se il punto P è in movimento, è possibile determinare la sua velocità nei due sistemi di riferimento che stiamo considerando. Indichiamo con v la velocità di P in S e con v’ la sua velocità misurata in S’; è possibile dimostrare che tra le due velocità sussistono le seguenti relazioni:

$ vec v = vec v’ + vec V , vec v’ = vec v – vec V $

Dove V indica la velocità con cui si muove il sistema di riferimento S’ rispetto a S.

All’inizio, molti scienziati sostenevano l’idea che la luce non avesse velocità, e che potesse compiere qualsiasi distanza senza impiegare tempo.

Galileo, invece, sosteneva che la luce avesse una velocità propria, ed elaborò un esperimento per dimostrarlo.

L’esperimento di Galileo

L’esperimento consisteva nel posizionare due uomini, ognuno dei quali con una lanterna, sulla cima di due collinette, ad una certa distanza l’una dall’altra.

All’inizio le due lanterne erano coperte, poi uno dei due uomini avrebbe dovuto scoprire la sua lanterna; l’altro avrebbe fatto altrettanto nel momento in cui avrebbe notato la luce sulla collinetta opposta.

In questo modo, Galileo avrebbe misurato il tempo trascorso dall’emissione del fascio di luce dal primo uomo alla ricezione del secondo, e conoscendo la distanza tra essi, avrebbe determinato la velocità della luce.

esperimenti-galilei — L’esperimento di Galilei

L’esperimento, però, non ebbe i risultati sperati; oggi sappiamo, infatti, che la velocità della luce è una grandezza troppo elevata perché possa essere confrontata con grandezze terrestri; i tempi di reazione degli uomini nell’esperimento sono assai maggiori del tempo che la luce impiega a percorre la distanza tra essi.

Secondo Galileo, però, le leggi ricavate dalle trasformazioni erano valide anche per la velocità della luce; di conseguenza, se un raggio di luce (che si propaga a velocità c) viene emesso da una navicella che si muove a velocità v, secondo Galileo la luce avrebbe viaggiato ad una velocità pari a c + v.

La teoria di Maxwell

Le equazioni di Maxwell, che descrivono il comportamento dei fenomeni elettrici e magnetici, hanno permesso di determinare con precisione il valore della velocità di propagazione della luce, pari a 299 792 458 m/s.

Tali equazioni permisero anche di dimostrare che il valore di questa velocità è indipendente dal sistema di riferimento che si sta considerando; tale valore, quindi, è lo stesso in qualunque sistema.

Di conseguenza, se un raggio di luce viene emesso da una navicella in movimento, la velocità di propagazione della luce non è influenzata dalla velocità della navicella, ma vale sempre c.

Potrebbero Interessarti

Video Lezioni: Relatività

L’esperimento di Michelson-Morley

Come abbiamo già visto, l’ipotesi della natura ondulatoria della luce fu giustificata con diversi esperimenti a metà dell’ottocento; tuttavia, solo con le equazioni di Maxwell fu possibile affermare che le onde luminose sono onde elettromagnetiche.

Fino ad allora, quindi, non era ben chiaro di che tipo di onde fossero quelle luminose, e si ipotizzò che esse si propagassero in un mezzo materiale particolare, definito etere luminifero, presente in tutto l’universo. Il moto della Terra e dei pianeti causava lo spostamento di questo etere, dando luogo al cosiddetto “vento d’etere”.

Si ipotizzò, quindi, che le equazioni dell’elettromagnetismo fossero applicabili alle onde luminose solo nel caso in cui il sistema di riferimento considerato fosse quello in cui l’etere fosse in quiete.

Per studiare, quindi, il moto delle onde luminose e calcolare così la velocità della luce, era necessario tener conto anche del vento d’etere causato dal moto della Terra attraverso questo mezzo.

I primi esperimenti a riguardo furono condotti dai fisici Michelson e Morley.

Il primo esperimento

Il primo che essi condussero prevedeva lo studio dell’interferenza della luce, generata da un fascio di luce monocromatica diretta su uno specchio semiriflettente, cioè tale da riflettere una parte dei raggi che lo colpiscono, e farsi attraversare da altri.

Ai lati di tale specchio (H) sono disposti altri tre specchi (A, B e C), sui quali vengono riflessi i raggi giungenti dal primo.

In particolare, i raggi di luce che partono dalla sorgente colpiscono H e vengono riflessi e proiettati in A e in B; da qui tornano indietro allo specchio H e vengono proiettati in C.

Esperimento di Michelson-Morley: fig. 1 — Figura 1

Analizzando il moto della luce nei tratti AH e BH (che sono uguali come distanze), e considerando anche la presenza del vento d’etere e idem moto della Terra, è stato possibile risalire alla velocità della luce.

Vediamo in dettaglio i tratti considerati.

Il tratto A-H

Nell’esperimento si utilizza come sistema di riferimento quello solare, e si suppone che la velocità della Terra (v) sia diretta nel senso negativo dell’asse y.

In questo modo, quando la luce percorre il tratto HA, la sua velocità, per le leggi della meccanica, ha modulo pari a (c – v), perché ha verso opposto a quello della velocità della Terra; nel tratto AH, invece, la velocità della luce e quella della Terra hanno stessa direzione e stesso verso, quindi la velocità della luce ha modulo (c + v):

Esperimento di Michelson-Morley: Fig. 2 — Figura 2

Se osservassimo la situazione dal sistema di riferimento terrestre, potremmo dire che la Terra è ferma, mentre è presente un vento d’etere che, nel primo caso ha velocità (di modulo v) opposta a quella della luce, mentre nel secondo caso ha velocità parallela a quella della luce.

Se indichiamo con l la distanza AH, è possibile determinare il tempo impiegato dalla luce nel percorrere il tratto AH e tornare indietro:

$ ∆t_1 = frac(l)(c – v) + frac(l)(c + v) = frac(2lc)(c^2 – v^2)$

Il tratto H – B

Nel tratto HB, il moto della luce è perpendicolare allo spostamento della Terra, e quindi anche alla direzione della velocità del vento d’etere; in questo caso, quindi, il vettore velocità della luce deve essere espresso come composizione di due vettori: la velocità risultante (diretta da H a B all’andata, e da B a H al ritorno), e la velocità del vento d’etere, opposta in verso a quella terrestre.

Esperimento di Michelson-Morley: fig. 3

Figura 3

La velocità risultante può essere ottenuta come se fosse il cateto di un triangolo rettangolo, in cui l’ipotenusa è data dal vettore velocità della luce, e l’altro cateto dal vettore velocità del vento d’etere.

Per cui si ha:

$ v_(ris) = sqrt(c^2 – v^2)$

Anche in questo caso, considerando lo spazio percorso da H a B e da B a H, pari a 2l, possiamo ricavare il tempo impiegato:

$ ∆t_2 = frac(2l)(v_(ris)) = frac(2lc)(sqrt(c^2 – v^2)) $

Conclusioni

Come possiamo notare, nonostante i tratti AH e BH siano uguali, i tempi di percorrenza della luce sono differenti. Questa differenza temporale da luogo a dei fenomeni di interferenza, che si generano quando i due fasci di luce vengono in contatto, e dipende da tale differenza e dai valori delle velocità.

I due tempi sarebbero uguali solo nel caso in cui la Terra fosse ferma, e quindi fosse assente anche il vento d’etere.

L’esperimento fu riproposto ipotizzando che l’apparato sperimentale si trovasse immerso nel mercurio, in modo che nel tratto BH la velocità della luce fosse parallela al vento d’etere, e nel tratto AH vi fosse perpendicolare.
In questo caso, si ricavò che nel tratto HB-BH il tempo di percorrenza era pari a $∆t1$, e nel tratto HA-AH pari a $∆t_2$.

Poiché è presente una differenza temporale, è naturale aspettarsi che, quando i fasci di luce si combinano, danno luogo ad una figura di interferenza diversa da quella dell’esperimento precedente (in questo caso, infatti, la differenza temporale è -( $∆t_1$ – $∆t_2$)) ; tuttavia, in questo caso non si registrò alcuna variazione nella figura di interferenza rispetto all’esperimento precedente.

Si concluse, quindi, che la teoria del vento d’etere non poteva essere valida per spiegare il moto della luce.

Potrebbero Interessarti

Video Lezioni: Relatività

La relatività ristretta

Nei primi anni del ‘900 le teorie sulla luce portavano degli scontri di opinione; era chiaro ormai che la luce avesse la stessa velocità in tutti i sistemi di riferimento inerziali, in disaccordo con la legge di composizione delle velocità di Galileo, e ancora non si poteva estendere il concetto di luce alla teoria di Maxwell; infatti questo avrebbe significato mettere in discussione le trasformazioni di Galileo e le nozioni di spazio e tempo assoluti.

Per risolvere il problema, quindi, nel 1905 Einstein formulò due leggi, che furono definiti principi della relatività ristretta; con essi si propose una nuova visione dell’Universo.

Primo principio della relatività ristretta: le leggi della fisica hanno la stessa forma in tutti sistemi di riferimento inerziali;

Secondo principio della relatività ristretta: la velocità della luce nel vuoto è la stessa in tutti i sistemi di riferimento inerziali, e non dipende dalla direzione di propagazione, e quindi dal moto della sorgente da cui è emessa.

Il secondo principio, noto anche come principio di invariata di c, spiega come mai l’esperimento di Michelson-Morley abbia dato risultati negativi: infatti, poiché la velocità della luce è indipendente dal sistema di riferimento, il tempo di percorrenza dei due tratti (quello verticale e quello orizzontale) deve essere lo stesso, e per questo non si registrarono variazioni nelle figure di interferenza.

La simultaneità

Nella fisica classica, enunciata da Newton, era stata presentata l’idea del tempo e dello spazio visti come entità assolute.

Einstein, invece, smentì l’ipotesi che esistesse una grandezza tempo assoluta, cioè che il tempo fosse identico in tutti i sistemi di riferimento e scorresse immutabile.

I ragionamenti di Einstein cominciarono dall’esaminare il concetto di simultaneità di due eventi, cioè il significato dell’affermazione che due eventi avvengano nello stesso istante.

Consideriamo, ad esempio, il procedimento che si può utilizzare per sincronizzare due orologi che si trovano il luoghi diversi e in quiete rispetto allo stesso sistema di riferimento; si inviano contemporaneamente due raggi di luce da ciascuno di essi, nella direzione del loro punto di mezzo.

Per definite la simultaneità possiamo utilizzare lo stesso procedimento della sincronizzazione degli orologi, considerando al loro posto il verificarsi di determinati eventi; nel momento esatto in cui accade l’evento, da esso viene odiato un raggio di luce nella direzione del punto di mezzo tra essi; se i raggi di luce inviati dalle posizioni dei due eventi raggiungono il punto centrale nello stesso momento, i due eventi si dicono simultanei.

Il concetto di simultaneità non ha validità assoluta; ciò significa che se due eventi sono simultanei in un determinato sistema di riferimento, non è detto che lo siano anche in un altro.

Per dimostrare questo concetto, Einstein elaborò un semplice esperimento.

L’esperimento di Einstein

Egli prese in considerazione due sistemi di riferimento inerziali diversi; uno quello di un osservatore fermo sulla Terra ( $O_1$ ), e l’altro quello di un osservatore posto in un treno in movimento a velocità costante ( $O_2$ ).

Ipotizziamo che nei punti A e B, equidistanti dal primo osservatore, nel momento esatto in cui l’osservatore $O_2$ si trovi a metà strada da essi, vengano emessi due raggi di luce.

esperimento-di-Einstein

Il punto di emissione dei raggi luminosi, fa si che essi raggiungano l’osservatore $O_1$ nello stesso istante; di conseguenza, per il primo osservatore gli eventi che si verificano nei punti A e B sono simultanei.

esperimento-di-Einstein

Per l’osservatore che si trova sul treno, invece, gli eventi non avvengono nello stesso momento; infatti, poiché il treno è in movimento, supponiamo verso sinistra, l’osservatore $O_2$ vede prima il raggio di luce emesso dal punto A, e successivamente quello emesso dal punto B; egli conclude, quindi, che i due eventi non sono simultanei.

esperimento-di-Einstein

Potrebbero Interessarti

Video Lezioni: Relatività

La dilatazione del tempo

Dal dilatazione del tempo è un fenomeno che può essere visto come conseguenza dei principi della Relatività.

Vediamo di cosa si tratta con un pratico esempio; consideriamo lo spazio che viene precorso da un raggio di luce emesso da una sorgente A e diretto in un punto B nel caso in cui la situazione è osservata in due sistemi di riferimento diversi, che sono in moto l’uno rispetto all’altro con velocità relativa v*; noteremo che il tempo impiegato dal raggio di luce nei due casi risulta diverso.

Sistema di riferimento con sorgente e ricevitore fermi

Inizialmente consideriamo un sistema di riferimento S’, in cui la sorgente A e il ricevitore B siano fermi, e posti ad una distanza L’ l’uno dall’altro, in posizione verticale.

dilatazione-del-tempo

Se misuriamo il tempo impiegato dal raggio di luce a nel percorrere il tratto da A a B, tornare indietro (da B ad A), il tempo che misuriamo sarà pari a:

$ ∆t_1 = frac(2L’)(c)$

In questo caso, poiché l’apparato è fermo sen sistema S’, l’emissione del raggio di luce dalla sorgente, e la ricezione finale del raggio, dopo che esso ha percorso la distanza 2L’, avvengono nello stesso punto A.

In questo caso, il tempo che impiega la luce a percorre tale tratto viene definito tempo proprio, e può essere misurato utilizzando un solo orologio posto nel punto A.

Sistema di riferimento in moto

Vediamo ora il secondo caso, in cui, nel sistema di riferimento S’, l’apparato visto precedentemente si sta muovendo a velocità v*. Di conseguenza, rispetto a S’ tutti i punti si muovono a velocità v*, compresi la sorgente A e il primo rivelatore B.

Sebbene il raggio di luce emesso da A si muove in linea retta da A a B, per un osservatore posto in S il percorso del raggio di luce apparirà differente; in particolare, il punto in cui il raggio di luce viene emesso è differente dal punto in cui viene visto tornare dopo aver percorso il suo tragitto.

dilatazione-dei-tempi

Per un osservatore in S, quindi, è come se il raggio di luce descrivesse un tragitto che può essere visto come l’ipotenusa di un triangolo rettangolo i cui cateti sono la distanza A-B e la distanza B-B’; chiamiamo tale ipotenusa con l.

In questo caso, quindi, il tempo che si misura dalla partenza del raggi di luce in A, all’arrivo del raggio di luce in A’’ è sicuramente diverso da quello misurato nel primo caso, in quanto la luce percorre uno spazio maggiore.

Il coefficiente di dilatazione

Si può dimostrare che tra i due intervalli di tempo sussiste la seguente relazione:

$ ∆t_2 = γ * ∆t_1 = frac(1)(sqrt(1 – (frac(v*)(c))^2 )) * ∆t_1 $

Il fattore γ si definisce coefficiente di dilatazione, e mostra di quanto il tempo rilevato dall’osservatore in S varia rispetto a quello dell’osservatore in S’.

Questa relazione è un’ulteriore prova che la velocità della luce non può essere raggiunta ne superata da nessun corpo; infatti, se la velocità v* diventasse molto grande, fino a raggiungere il valore di c, avremmo al denominatore della frazione il valore 0, e ciò è impossibile.

Inoltre, se v* fosse maggiore di c, il rapporto v*/c sarebbe maggiore di 1, e ciò implicherebbe un valore negativo all’interno della radice quadrata, cosa che non può verificarsi per un valore temporale.

La dilatazione dei tempi, quindi, mostra che la durata di un fenomeno è minima se essa viene misurata nel sistema di riferimento solidale con il sistema dei corpi che stiamo considerando, e nel quale ha inizio il fenomeno.

Orologi in posizioni diverse

Ipotizziamo ora di voler misurare la durata del tempo da orologi posti in posizioni diverse.

Il primo orologio ( $O_1$ ) è posto sull’apparecchiatura che si muove a velocità v*, ed è quello che misura il tempo $∆t_1$ . Altri due orologi sono fermi nelle posizioni che verranno occupate dall’apparecchio durante il suo moto, e che abbiamo denotato con A’ (in cui si trova $O_2$ ) e A’’ (in cui si trova $O_3$ ).

Confrontando le rilevazioni effettuate dagli orologi fermi e dall’orologio in moto; possiamo affermare che quest’ultimo ritarda rispetto agli orologi fermi e sincronizzati in S.

Si può dire, quindi, che per un osservatore posto in S il tempo che si misura in S’ sembra scorrere più lentamente che in S’.

Potrebbero Interessarti

Video Lezioni: Relatività

La contrazione delle lunghezze

Quando la velocità di un corpo diventa molto elevata, e può essere approssimata alla velocità della luce, la dilatazione del tempo non è l’unico fenomeno che si può individuare; anche le lunghezze dei corpi vengono modificate.

Per capire le implicazioni di questa affermazione, dobbiamo definire due tipi di lunghezze riferite al corpo che stiamo considerando, la lunghezza propria e la lunghezza impropria del corpo.

Lunghezza propria e impropria

La lunghezza propria, indicata con $L_0$, è la lunghezza di un corpo a riposo, cioè a velocità nulla; si può anche definire come la distanza tra due punti misurata in un sistema di riferimento che è in quiete rispetto ad essi.

La lunghezza impropria di un corpo ( $L$ ), invece, è la lunghezza contratta, che si ha quando il corpo si sta muovendo a velocità v. La lunghezza di un segmento che si sta muovendo, quindi, può essere definita come il prodotto della velocità v a cui si sta spostando il segmento per l’intervallo di tempo necessario affinché i due estremi del segmento passino per uno stesso punto fisso.

Cerchiamo una formula generale che possa esprimere una relazione tra le due lunghezze attraverso un esempio.

Esempio

Consideriamo due osservatori posti in sistemi di riferimento differenti; il primo (A) è fermo sulla Terra, mentre il secondo (B) si sta muovendo a velocità v, prossima a quella della luce, verso una stella lontana; consideriamo il tempo impiegato dal secondo osservatore per approdare sulla stella.

Per l’osservatore in moto il tempo misurato è un tempo proprio, in quanto esso si trova in un sistema di riferimento solidale con la durata del fenomeno; di conseguenza esso misura un tempo $∆t_0$.

Per l’osservatore A, invece, il tempo misurato, ∆t, è un tempo improprio. Egli misurerà una lunghezza propria della distanza che B percorre, in quanto A è fermo rispetto alla navicella in moto; mentre la lunghezza misurata da B sarà una lunghezza contratta.

La distanza misurata dall’osservatore sulla Terra vale quindi $L_0 = v * ∆t$, mentre quella misurata dall’osservatore in moto vale $L = v * ∆t_0$. Poiché per entrambi gli osservatori la velocità è la stessa, possiamo uguagliare le due espressioni e ricavare così la relazione cercata:

$ v = frac(L_0)(∆t) , v = frac(L)(∆t_0) to L = frac(L_0)(∆t) * ∆t_0 = L_0 * frac(∆t_0)(∆t)$

Dalla formula della dilatazione del tempo, possiamo ricavar il rapporto tra il tempo proprio e quello improprio, e così la formula precedente diventa:

$L = L_0 * frac(∆t_0)(∆t) = L_0 * sqrt(1 – frac(v^2)(c^2))$

Esempio

Consideriamo due gemelli, dei quali uno, Luca, viaggia verso una stella lontana ad una certa velocità $v=0,990 c$, prossima a quella della luce; l’altro, Paolo, è fermo sulla Terra.

Conoscendo la distanza della stella dalla Terra, sappiamo che Luca percorre una distanza di 26,4 anni-luce; il tempo impiegato da Luca nel percorrere questa distanza è relativo, varia in base all’osservatore che lo misura.

Poiché Paolo misura la durata del fenomeno in un sistema di riferimento che non è solidale con esso (la partenza è sulla Terra, mentre l’arrivo è su una stella), il tempo misurato da Paolo è un tempo improprio $∆t$, mentre quello misurato da Luca è un tempo proprio $∆t_0$.

Per l’osservatore sulla Terra, il viaggio dura circa 26,4 anni:

$∆t_0 = frac(L)(v) = frac(26,4 al)(0,990 c) = 26,4 a$

Per l’osservatore in movimento, invece, il tempo si può ricavare con la formula della dilatazione dei tempi:

$ ∆t = ∆t_0 * sqrt(1 – frac(v^2)(c^2)) = 3,77 a$

Dato che la velocità relativa tra la stella e la Terra è quella a cui si sta muovendo Luca, cioè $0,990 c$, per l’osservatore in movimento la distanza tra i due corpi è minore rispetto a quella misurata da Paolo.

In questo caso, quindi, l’osservatore sulla Terra misura una distanza con l’osservatore in movimento che è una lunghezza propria, mentre quella misurata dall’osservatore in moto, è una lunghezza impropria e contratta; possiamo trovare il suo valore utilizzando la formula vista precedentemente:

$ L = L_0 * sqrt(1 – frac(v^2)(c^2)) = 26,4 al * sqrt(1 – frac((0,990 c)^2)(c^2)) = 3,73 al $

Potrebbero Interessarti

Video Lezioni: Relatività

Le trasformazioni di Lorentz

Come abbiamo visto nel caso della meccanica classica, esistono delle formule che permettono di descrivere il moto di un punto materiale relativamente a due sistemi di riferimento inerziali differenti; in particolare, i due sistemi di riferimento inerziali possono essere l’uno in moto rispetto all’altro.

Detto S il sistema di riferimento inerziale fermo, con origine in O e assi x e y, e S’ il sistema di riferimento inerziale, con origine in O’ e assi x’ e y’, in moto rispetto al primo con velocità v, le equazioni che descrivono il moto di un punto P nei due sistemi di riferimento sono dette trasformazioni di Galileo, e sono le seguenti:

${(vec s = vec s’ + vec v * t), (t = t’):} , {(vec s’ = vec s – vec v * t), (t’ = t):} $

Queste leggi, però, non possono essere utilizzate nell’ambito della relatività, in quanto come abbiamo visto, nel caso di velocità molto elevate e prossime a quelle della luce, si ha una dilatazione dei tempi e una contrazione delle lunghezze in base al sistema di riferimento considerato.

Per questo, le equazione di trasformazione che si utilizzano sono differenti, e sono state formulate dal fisico olandese Lorentz; egli suppose che tali trasformazioni fossero quelle per cui le equazioni dell’elettromagnetismo rimangano invariate nel passaggio da un sistema di riferimento ad un altro, in moto relativo rispetto al primo.

Le leggi a cui facciamo riferimento, quindi, vengono definite trasformazioni di Lorentz, e hanno la seguente forma:

${(x’ = frac(x – vt)(sqrt(1 – frac(v^2)(c^2))) = γ * (x – vt)), (t’ = frac(t – frac(vx)(c^2))(sqrt(1 – frac(v^2)(c^2))) = γ *(t – frac(vx)(c^2))):}$

In questo caso, x’ indica lo spostamento nel sistema di riferimento S’, cioè quello in moto rispetto ad S, e t’ indica il tempo misurato in tale sistema di riferimento.

Applicazioni delle trasformazioni di Lorentz

Vediamo ora alcune applicazioni della formula di trasformazione di Lorentz che mettano in evidenza il fenomeno della dilatazione dei tempi e della contrazione delle lunghezze.

Supponiamo che un determinato fenomeno A avvenga nel sistema di riferimento S all’istante di tempo $t = 0$ e alla posizione $x = 0$, mentre un altro fenomeno B avvenga in S in un tempo successivo, che chiamiamo $t_0$, sempre nell’origine.

Indichiamo l’intervallo di tempo che separa due fenomeni con $∆t=t_0$ .

Consideriamo ora il sistema di riferimento S’, in moto rispetto ad S; il primo fenomeno A avviene sempre nell’origine del sistema, cioè in $x’ = 0$ al tempo $t’ = 0$; la posizione in cui avviene il fenomeno B può essere calcolata con le formule di trasformazione di Lorentz:

$ x’ = γ * (x – vt) = γ * (0 – vt) = – γvt $

Allo stesso modo calcoliamo ora l’istante di tempo in cui avviene il fenomeno:

$ t’ = γ * (t_0 – frac(vx)(c^2)) = γ * (t_0 – 0) = γ * t_0$

Nel sistema di riferimento S’, quindi, l’intervallo di tempo ∆t’ che intercorre tra i due eventi è dato da:

$∆t’ = t’ = γ * t_0 = γ * ∆t$

Vediamo quindi che nel sistema di riferimento S’ l’intervallo di tempo che separa i due eventi è maggiore dell’intervallo che si ha nel sistema S, in accordo con la dilatazione del tempo previsto dalla teoria della relatività.

Vediamo ora il caso di una sbarretta di lunghezza ∆x nel sistema di riferimento S, ferma rispetto ad esso. Vogliamo conoscere la lunghezza della sbarretta nel sistema S’, che si muove a velocità v, verso destre, rispetto ad S.

Supponiamo che all’istante di tempo $t = 0$ e $t’ = 0$ le origini dei due sistemi di riferimento coincidano. Per determinare la lunghezza ∆x’ della sbarra nel sistema S’ dobbiamo determinare le posizioni che vengono assunte dall’estremo nell’istante iniziale e nell’istante finale, quando tale estremo si viene a trovare in O’ (infatti, nel sistema S’ si vede la sbarra muoversi con velocità v verso sinistra).

Utilizzando le trasformazioni di Lorentz, possiamo determinare la coordinata x’ dell’estremo destro e il tempo t’ corrispondente a tale posizione:

${(x’ = γ * (x – vt) = γ * (∆x – vt)), (t’ = γ * (t – frac(vx)(c^2)) = γ * (t – frac(v)(c^2) * ∆x)):}$

Possiamo determinare la lunghezza della sbarra considerano il momento in cui l’estremo destro di essa passa per l’origine O’; in questo caso si ha x’ = 0. Sostituendo questa espressione della prima equazione troviamo:

$ 0 = γ * (∆x – vt) to t = frac(∆x)(v)$

Sostituendo questa espressione nella seconda equazione otteniamo:

$ t’ = frac(∆x)(vγ)$

Nel sistema di riferimento S’, la sbarretta si sta spostando verso sinistra con velocità v; di conseguenza, il tempo t’ che l’estremo destro impiega per passare dalla posizione x’ alla posizione $x’ = 0$ è dato dal rapporto $∆x’/v$.

Confrontando questa espressione con l’espressione precedente per t’, troviamo una relazione tra le lunghezze della sbarretta misurate nel due sistemi di riferimento:

${(t’ = frac(∆x)(vγ)), (t’ = frac(∆x’)(v)):} to ∆x’ = frac(∆x)(γ) $

In accordo con la relatività ristretta, vediamo che la misura della lunghezza in S’ risulta minore di quella misurata in S.

Potrebbero Interessarti

Video Lezioni: Relatività

L’intervallo invariante

In fisica, molto spesso, per rappresentare un determinato fenomeno, si utilizza un sistema di riferimento con assi coordinati.

Ad esempio, si può utilizzare un sistema di riferimento spazio-tempo, che è quindi bidimensionale; altrimenti un sistema di riferimento con più coordinate, in base al numero di dati che si vogliono rappresentare.

Solitamente si utilizza un grafico tridimensionale $(x, y, z)$ per descrivere la posizione del corpo che si vuole studiare, e si aggiunge poi la variabile temporale t per descrivere l’istante di tempo in cui il corpo si trova in una certa posizione.

L’intera quaterna $(t, x, y, z)$ è quella che definisce l’intero evento.

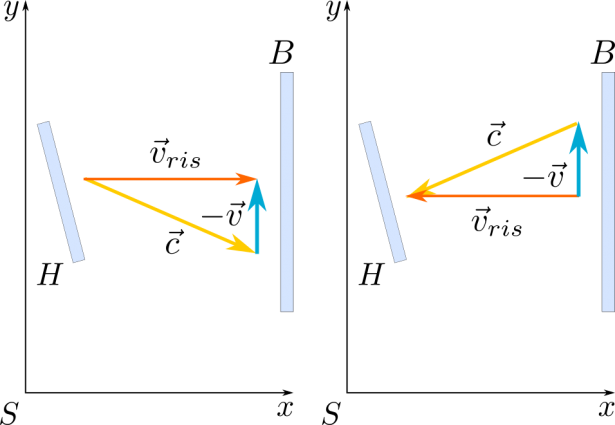
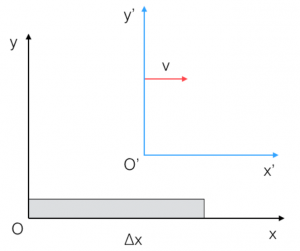
Per introdurre in concetto di intervallo invariante, consideriamo inizialmente due sistemi di riferimento bidimensionali, dei quali il primo è (x, y), il classico sistema di riferimento cartesiano, mentre il secondo $(X, Y)$ è un sistema di riferimento in cui gli assi sono ruotati di un angolo α rispetto al precedente.

Consideriamo sugli assi dei due sistemi di riferimento rispettivamente i vettori ∆x, ∆y, ∆X, ∆Y, che descrivono, nei propri sistemi, lo stesso vettore spostamento ∆s:

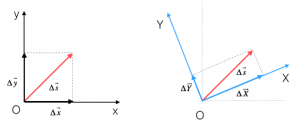
sistemi-di-riferimento

In entrambi i casi, il modulo del vettore spostamento può essere determinato utilizzando il teorema di Pitagora, a partire dai suoi vettori componenti; per il primo sistema di riferimento abbiamo quindi:

$ (∆x)^2 + (∆y)^2 = (∆s)^2$

e per il secondo sistema di riferimento abbiamo:

$ (∆X)^2 + (∆Y)^2 = (∆s)^2$

Poiché il modulo del vettore spostamento è lo stesso in entrambi i casi, possiamo uguagliare le due espressioni precedenti e otteniamo:

$ (∆x)^2 + (∆y)^2 = (∆X)^2 + (∆Y)^2$

Quindi, anche se cambiamo sistema di riferimento, e anche se cambiano i vettori componenti che descrivono uno stesso vettore ∆s, la somma dei quadrati dei moduli dei suoi vettori componenti nei vari sistemi è invariante, cioè è sempre uguale.

Possiamo estendere il ragionamento al caso di un sistema tridimensionale, in cui cioè compare un terzo asse; nel primo sistema di riferimento avremo l’asse z, su cui individuiamo il vettore componente ∆z, mentre sul secondo sistema di riferimento consideriamo l’asse Z con vettore componente ∆Z.

Nell’uguaglianza, quindi, dobbiamo aggiungere anche il quadrato della componente del vettore spostamento lungo il terzo asse:

$ (∆x)^2 + (∆y)^2 + (∆z)^2 = (∆X)^2 + (∆Y)^2 + (∆Z)^2$

Il concetto di intervallo invariante si utilizza nell’ambito della relatività ristretta, dove però si considera anche un’intervallo di tempo ∆t per descrivere un determinato fenomeno.

Si definisce, quindi, il quadrato dell’intervallo invariante per la relatività ristretta la seguente quantità:

$ (∆σ)^2 = (c * ∆t)^2 – (∆x)^2 – (∆y)^2 – (∆z)^2 $

Dove le quantità ∆x, ∆y, ∆z rappresentano gli incrementi di coordinate che separano due eventi distinti.

L’intervallo invariante, quindi, è dato dalla radice quadrata dell’espressione precedente:

$∆σ = sqrt((c * ∆t)^2 – (∆x)^2 – (∆y)^2 – (∆z)^2)$

Esaminiamo il caso particolare in cui il sistema di riferimento considerato è solidale con il fenomeno; di conseguenza, le coordinate che rappresentano l’inizio del fenomeno e la sua fine hanno le stesse coordinate spaziali, e quindi gli incrementi ∆x, ∆y e ∆z sono nulli. L’intervallo di tempo ∆t coincide proprio con il tempo proprio del fenomeno, e quindi la formula precedente assume una semplice espressione, e l’intervallo invariante è dato dal prodotto dell’intervallo di tempo per la velocità:

$∆σ = sqrt((c * ∆t)^2 – (∆x)^2 – (∆y)^2 – (∆z)^2) = sqrt((c * ∆t)^2 – (0)^2 – (0)^2 – (0)^2) = sqrt((c * ∆t)^2 ) = c * ∆t$

Esercizio

Consideriamo un’astronave che viaggia verso una stella distante 25 anni-luce dal Sole; sapendo che la durata del viaggio prevista è di circa 28 anni, calcolare la velocità a cui si muove l’astronave e la durata del viaggio misurata dall’astronave.

Conoscendo la distanza della stella dal Sole, e il tempo impiegato dall’astronave per raggiungerla, possiamo facilmente calcolare la velocità a cui viaggia l’astronave:

$ v = s/t = frac(25 al)(28 a) = 0,89 (al)/(a) = 0,89 c$

Per il secondo quesito, consideriamo il sistema di riferimento dell’astronave: rispetto ad esso, la partenza e l’arrivo avvengono nello stesso luogo, quindi la durata del viaggio rispetto all’astronave sarà uguale al tempo proprio.

Se consideriamo l’asse x quello su cui giace la retta che passa per il Sole e la stella, l’incremento ∆x corrisponde alla distanza della stella dal Sole.

Dall’equazione dell’intervallo invariante, sappiamo che nei sistemi di riferimento dell’astronave e della Terra, l’intervallo ∆s è lo stesso. Nel sistema di riferimento dell’astronave l’intervallo invariante è dato dalla formula:

$∆σ = c * ∆τ$

dove τ indica il tempo proprio;

mentre rispetto alla Terra si ha la seguente formula:

$∆σ = sqrt((c * ∆t)^2- (∆x)^2) $

dove ∆t indica il tempo in anni impiegato dalla navicella a compiere il tragitto, mentre ∆x è la distanza percorsa.

Uguagliando le due espressioni possiamo ricavare il valore del tempo proprio:

$ ∆τ = frac( sqrt((c * ∆t)^2- (∆x)^2))(c)$

Sostituiamo i valori numerici:

$ ∆τ = frac( sqrt((c * ∆t)^2- (∆x)^2))(c) = frac( sqrt((1 * 28)^2- (25)^2))(1) = 12,6 a $

Potrebbero Interessarti

Video Lezioni: Relatività

Lo spazio-tempo di Minkowski

I sistemi di riferimento a quattro dimensioni

Il concetto di spazio-tempo è strettamente legato a quello di intervallo invariante; come abbiamo già visto, mentre in fisica classica gli spazi utilizzati per descrivere i fenomeni hanno due o tre dimensioni, e servono generalmente per individuare la posizione di un determinato corpo, nel caso della relatività è necessario tenere in considerazione anche il fattore tempo.

Per questo, si utilizzano dei sistemi di riferimento che presentano sia delle coordinate spaziali, sia delle coordinate temporali, per individuare la posizione di un corpo in un certo istante di tempo.

I sistemi di riferimento di questo tipo descrivono uno spazio a quattro dimensioni, che viene definito spazio-tempo, o anche spazio di Minkowski.

Uno spazio a quattro dimensioni è un concetto puramente matematico, e non ha proprietà fisiche; ogni punto che appartiene a tale spazio rappresenta un evento, e viene definito quindi punto-evento.

Anche in questo caso, è valido il concetto di intervallo invariante; se consideriamo due eventi, sappiamo che la differenza di coordinate che li descrivono varia in base al sistema di riferimento scelto, ma l’intervallo invariante è lo stesso in tutti i sistemi di riferimento inerziali. Ricordiamo che l’espressione di intervallo invariante è la seguente:

$ (∆σ)^2 = (c * ∆t)^2 – (∆x)^2 – (∆y)^2 – (∆z)^2$

L’intervallo invariante può essere considerato, nello spazio-tempo, al pari di un vettore spostamento di un normale sistema di riferimento.

L’intervallo invariante nello spazio-tempo

L’intervallo invariante può essere positivo, negativo o nullo, e in base a questo si parla di intervallo di tipo tempo, di tipo spazio, o di tipo luce.

Nel primo caso, considerando due eventi A e B, esiste un sistema di riferimento in cui gli eventi avvengono nello stesso luogo con un certo intervallo di tempo che li separa; nel secondo caso, invece, esiste un sistema di riferimento in cui gli eventi A e B avvengono nello stesso istante, ma in luoghi diversi.

Infine, nel terzo caso gli eventi sono separati da un intervallo di tipo luce, cioè esiste un raggio di luce che collega l’evento A con l’evento B.

Le componenti del vettore sono quattro, una per ogni dimensione dello spazio-tempo. Avremo quindi tre componenti spaziali (quelle relative agli assi x, y e z) e una componente temporale (quella lungo t).

I vettori di questo tipo sono definiti quadrivettori, o tetravettori, in quanto sono costituiti da una quaterna ordinata. Tuttavia, poiché spazio e tempo non sono grandezze omogenee, e quindi non possono essere sommate tra loro, le coordinate di un punto appartenente allo spazio di Minkowski vengono rappresentate in questo modo: (x, y, z, ct), dove c è la velocità della luce.

Il modulo del vettore in questo caso, cioè il quadrato della sua lunghezza, è dato dal quadrato della componente temporale a cui vengono sottratti i quadrati delle componenti spaziali.

La linea d’universo

Per semplicità, consideriamo uno spazio-tempo bidimensionale, in cui compare la coordinate temporale e la coordinata spaziale x; costruiamo in grafico ponendo la coordinate x come ascissa, mentre la coordinata ct come ordinata.

In un grafico di questo tipo, il moto di una qualsiasi particella è una curva, che viene definita linea d’universo; l’asse spaziale, quindi, rappresenta la linea d’universo di un oggetto fermo, mentre l’asse temporale rappresenta l’insieme di tutti gli eventi che avvengono simultaneamente ad un evento dato, preso come riferimento.

Il cono di luce

Una retta inclinata di 45° rispetto l’asse delle ascisse, cioè una retta di equazione $ct = x$ , rappresenta la linea d’universo di una particella che si muove alla velocità della luce.

A partire da questa retta, e considerando uno spazio tridimensionale, possiamo costruire il cosiddetto cono di luce:

Cono-di-luce-costruito — Cono di luce costruito a partire da una linea d’universo.

Il moto di particelle dotate di massa è rappresentato da curve, ovvero linee d’universo, che sono contenute interamente all’interno del cono di luce, e non ne fuoriescono mai. Le linee d’universo, invece, che giacciono sulla superficie del cono sono quelle che rappresentano i raggi di luce.

Potrebbero Interessarti

Video Lezioni: Relatività

Equivalenza massa-energia

La fisica classica prevede che l’energia possa essere espressa in varie forme (cinetica, potenziale, …), ma che in generale essa si conserva; anche la massa di un sistema si conserva in seguito ad un certo fenomeno fisico per la legge di Lavoisier; tale legge prevede, infatti, che in una qualsiasi reazione chimica la massa dei reagenti deve essere uguale a quella dei prodotti.

Nella teoria della relatività, però, anche queste affermazioni perdono validità; Albert Einstein, infatti, affermò che la massa e l’energia sono quantità fisiche collegate tra loro, e in particolare il rapporto che c’è tra esse dipende dal quadrato della velocità della luce nel vuoto.

Questa relazione si traduce nella famosa formula:

$ E = m * c^2 $

dove E indica l’energia complessiva del corpo in questione (espressa in J), cioè la somma di tutte le energie che esso possiede; m indica la massa del corpo a riposo (espressa in kg); c è la velocità della luce nel vuoto (espressa in m/s).

Da questa relazione si può dedurre che la massa di un corpo non si conserva come prevedeva la fisica classica, ma varia in base alle variazioni di energia cui il corpo è sottoposto.

Di conseguenza, se il corpo assorbe energia si avrà un aumento della sua massa; se esso cede energia, invece, anche la massa subisce una diminuzione.

La massa di un corpo, quindi, è in ogni caso una forma di energia; qualsiasi corpo, quindi, che ha massa possiede una quantità di energia pari a $mc^2$.

Energia di un corpo a riposo

Si definisce l’energia di un corpo a riposo come il prodotto del quadrato della velocità per la massa a riposo del corpo:

$ E_0 = m_0 * c^2 $

In generale un corpo in movimento, possiede energia cinetica; quindi, l’energia totale del corpo sarà data dalla somma di tutte le energie che esso possiede:

$ E = m_0 * c^2 + 1/2 m_0 * v^2 = m_0 * c^2 (1 + 1/2 frac(v^2)(c^2))$

L’espressione tra parentesi può essere approssimata, ( nel caso in cui la velocità v è molto piccola rispetto a c), come coefficiente di dilatazione γ; l’equazione generale dell’energia, quindi, assume la seguente forma:

$ E = frac(m_0 c^2)(sqrt(1 – frac(v^2)(c^2))) = m_0 * c^2 γ $

Rappresentando il grafico dell’energia E in funzione della velocità v, notiamo che la curva presenta un asintoto verticale v = c;

grafico-energia-velocità

possiamo dedurre, quindi, che se la velocità del corpo si avvicina a quella della luce, la sua energia aumenta, fino a raggiungere un valore infinito.

Ciò significa che un corpo si può muovere alla velocità della luce solo se esso possiede una quantità infinita di energia; dato che ciò non è possibile nella realtà, otteniamo un’ulteriore conferma del fatto che velocità della luce non può essere raggiunta da nessun corpo che possiede massa, e rappresenta quindi una velocità limite.

L’energia cinetica relativistica

Conoscendo l’espressione generale dell’energia totale di un corpo, possiamo definire l’energia cinetica relativistica; essa corrisponde alla differenza tra l’energia totale e l’energia che il corpo possiede quando è fermo, cioè l’energia a riposo del corpo.

L’energia cinetica, quindi, assume la seguente espressione:

$ k = m_0 * c^2 γ – m_0 * c^2 = m_0 * c^2 ( γ – 1) $

A partire dall’energia totale, inoltre, possiamo anche definire la massa relativistica di un corpo; essa è data dal prodotto della massa a riposo del corpo per il coefficiente γ:

$ m = m_0 * γ $

Vediamo, quindi, che con il variare della velocità del corpo, non solo si modificano tempi e lunghezze, ma anche la massa subisce variazioni. Mano a mano che la velocità diminuisce, la massa del corpo diventa sempre più piccola; per v=0 si raggiunge il valore minimo, corrispondente a quello della massa a riposo.

Come sappiamo, per un corpo che ha massa e si muove a velocità v, possiamo definire la quantità di moto del corpo come prodotto della massa per la velocità. Avendo introdotto il concetto di massa relativistica, è naturale parlare anche di quantità di moto relativistica, che si esprime come:

$ p = mv = m_0 * γ * v = frac(m_0 * v)(sqrt(1 – frac(v^2)(c^2)))$

Potrebbero Interessarti

Video Lezioni: Relatività

L’effetto doppler relativistico

Come abbiamo visto nel caso delle onde sonore, se la sorgente che emette il suono e il rilevatore che lo riceve sono in moto relativo tra loro, la frequenza o la lunghezza d’onda del segnale che viene percepito dall’osservatore varia. In questo modo, l’osservatore può capire se la sorgente si sta allontanando o avvicinando in base al suono che percepisce.

Ricordiamo che vi sono delle relazioni tra le frequenze percepite e quelle emesse; in generale, se la sorgente e l’osservatore si muovono sulla stessa retta e si stanno avvicinando, la frequenza che l’osservatore percepisce è data dalla formula:

$v’ = v * frac(1 + frac(V_R)(V_o))(1 – frac(V_S)(V_o))$

dove v è la frequenza emessa dall’onda, mentre $Vr$, $V_s$ e $V_o$ sono, rispettivamente, le velocità del rilevatore, della sorgente e dell’onda.

Nel caso in cui il rilevatore e la sorgente si stiano allontanando, invece, la formula è la seguente:

$v’ = v * frac(1 – frac(V_R)(V_o))(1 + frac(V_S)(V_o))$

L’effetto doppler e le onde luminose

L’effetto doppler si manifesta anche nel caso di onde luminose; in astronomia, ad esempio, questo fenomeno è studiato per capire se le galassie sono in allontanamento o in avvicinamento.

Nel caso di onde luminose, però, le formule che permettono di determinare le nuove frequenze percepite dal rilevatore sono diverse. Per prima cosa, mentre per le onde sonore la velocità di propagazione dell’onda dipende dalla velocità della sorgente, nel caso della luce, non potendo applicare la legge di composizione delle velocità, da velocità dell’onda è sempre la stessa, indipendentemente dal fatto che la sorgente sia ferma o in moto.

Inoltre, poiché la luce si propaga nel vuoto, e non in un mezzo, non è possibile capire se a muoversi sia la sorgente o l’osservatore, e quindi si parla di velocità relativa osservatore-sorgente.

Si può dimostrare che la frequenza v’ del segnale che viene percepita dall’osservatore nel caso in cui osservatore e sorgente si allontanano è data dalla seguente formula:

$ v’ = v * frac(sqrt(1 – frac(V_r)(c)))(sqrt(1 + frac(V_r)(c))) = frac(sqrt(1 – β))(sqrt(1 + β))$

con Vr = velocità relativa osservatore-sorgente. In questo caso, quindi, la frequenza rilevata è minore di quella emessa.

Nel caso in cui, invece, l’osservatore e la sorgente siano in avvicinamento, la formula vale con i segni invertiti:

$ v’ = v * frac(sqrt(1 + frac(V_r)(c)))(sqrt(1 – frac(V_r)(c))) = frac(sqrt(1 + β))(sqrt(1 – β))$

In questo caso, invece, la frequenza rilevata è maggiore di quella emessa.

L’effetto doppler e le galassie

Come accennato precedentemente, lo studio dell’effetto doppler nel caso di onde luminose è particolarmente utilizzato in astrofisica, in quanto esso rappresenta uno dei pochi modi che si hanno per studiare le galassie, e per capire se esse sono in avvicinamento o in allontanamento rispetto alla Via Lattea, e determinare la velocità a cui si spostano.

Questo studio si basa sul fatto che lo spettro emesso dalle stelle è uno spettro a righe di assorbimento; l’effetto doppler si manifesta quando, esaminando lo spettro emesso da una stella, si notano righe di assorbimento che si trovano in posizioni diverse rispetto rispetto allo stesso spettro misurato in laboratorio.

Si deduce, quindi, che vi è una variazione della lunghezza d’onda, e quindi della frequenza che vengono percepite; in particolare, poiché lo spettro del visibile presenta come colori marginali il blu e il rosso, si parla di “spostamento verso il rosso”, o redshift se lo spettro presenta righe spostate verso lunghezze d’onda maggiori:

redshift

altrimenti si parla di “spostamento verso il blu”, o blueshift nel caso di spostamento verso lunghezze d’onda minori.

blueshift

Si definisce, quindi, il numero puro z, dato da:

$ z = frac(v)(v’) – 1 $

Tale numero permette di capire, a partire dalle frequenze emessa e percepita, se la sorgente si sta avvicinando o allontanando dall’osservatore: in caso di redshift si hanno valori positivi di z, mentre in caso di blueshift si hanno valori negativi.

Nel caso in cui z = 0, la frequenza percepita è uguale alla frequenza emessa, e quindi l’osservatore e la sorgente sono in quiete.

Potrebbero Interessarti

Video Lezioni: Relatività

La relatività generale

La teoria della relatività generale estende le nozioni della relatività ristretta ai sistemi di riferimento non inerziali, cioè quei sistemi che, rispetto ad un sistema di riferimento inerziale, sono sottoposti ad un’accelerazione.

La relatività generale si basa su alcuni principi, alcuni dei quali ottenuti sulla base di esperimenti ideali.

Il primo principio della relatività generale, definito principio di equivalenza, venne formulato in due versioni successive, una versione “debole” e una versione “forte”; la prima formulazione asserisce che:

la massa inerziale di un corpo e la massa gravitazionale sono numericamente uguali, dove per massa inerziale si intende la proprietà del corpo di opporsi alla variazione di moto, mentre per massa gravitazionale la sua proprietà di subire l’influsso del campo gravitazionale.

La seconda formulazione, invece, è la seguente:

in un campo gravitazionale è sempre possibile scegliere un sistema di riferimento che sia localmente inerziale, cioè in cui esiste un intorno sufficientemente piccolo del punto in cui è possibile eliminare l’effetto di una forza di gravità costante. In quell’intorno, quindi, si possono utilizzare le stesse leggi del moto che si utilizzano in assenza di gravità.

Questa seconda formulazione assume un rilievo particolare, ed è stata ottenuta a partire da un’esperimento ideale noto come ascensore di Einstein.

L’ascensore di Einstein

Per questo esperimento si considera un’osservatore chiuso all’interno di una cabina, senza possibilità di veder l’ambiente circostante.

Esaminiamo due situazioni possibili:

ascensore-di-einstein — L’ascensore di Einstein: nel primo caso l’ascensore è in quiete sulla Terra; nel secondo subisce un’accelerazione verso l’alto.

Nel primo caso la cabina si trova in quiete in un sistema di riferimento inerziale, supponiamo quello terrestre, in cui è presente un’accelerazione di gravità g.

Se l’osservatore lascia cadere un’oggetto, nota che esso cade sul fondo della cabina con un’accelerazione di $g = 9,8 m/s^2$ dovuta al campo gravitazionale.

Nel secondo caso, invece, la cabina è posta all’interno di una navicella che si muove con accelerazione costante pari a g; anche in questo caso, se l’osservatore lascia cadere una pallina, questa raggiungerà il fondo della navicella con la stessa accelerazione con cui essa si muove, spinta dalla forza apparente dovuta all’accelerazione.

Di conseguenza, in entrambi i casi la pallina cade con la stessa accelerazione; nel primo caso ci troviamo in un sistema di riferimento inerziale (quello terrestre), nel secondo in un sistema di riferimento non inerziale, perché accelerato (quello della navicella).

Il secondo principio della relatività generale

Da questo esempio possiamo ricavare anche un altro importante principio, definito secondo principio della relatività generale.

Tale principio può essere considerato una generalizzazione del primo assioma della relatività, che affermava che le leggi della fisica sono le stesse in tutti i sistemi di riferimento inerziali.

Il principio, infatti, asserisce che le leggi della fisica hanno la stessa forma in tutti i sistemi di riferimento, inerziali e non.

Abbiamo visto, con l’ascensore di Einstein, che si presenta la stessa situazione sia nel caso della cabina posta nel sistema di riferimento inerziale della Terra, sia nella cabina in accelerazione costante.

Ciò significa che gli effetti che sono provocati da un’accelerazione costante du un determinato corpo sono gli stessi che sullo stesso corpo (fermo) sono provocati da un campo gravitazionale uniforme. Di conseguenza, in entrambi i casi possono essere applicate lei fisiche con la stessa forma.

I raggi di luce in sistemi di riferimento accelerati

Inoltre, con tale principio viene a cadere anche l’assioma sulla costanza della velocità della luce; i raggi di luce che vengono emessi in un sistema di riferimento accelerato che viene osservato da un sistema di riferimento fisso, non si propagano in traiettoria rettilinea, ma appaiono curvati.

esperimento-navicella

Di conseguenza, il modulo della velocità rimane costante, ma la direzione e il verso del vettore velocità cambia in ogni punto della traiettoria.

Potrebbero Interessarti

Video Lezioni: Relatività

La curvatura dello spazio-tempo

Con la teoria della relatività generale furono impiegati dei nuovi modelli geometrici, scoperti a partire dai primi anni dell’ottocento, definiti geometrie non euclidee. In base a queste nuove geometrie fu possibile introdurre il concetto di spazio curvo, e in particolare di geometrie sferiche, ellittiche, iperboliche, ecc.

Sulla base di questi concetti matematici, fu possibile per Einstein formulare altri due concetti di grande importanza.

La presenza di masse incurva lo spazio-tempo

Il primo concetto consiste nell’affermare che la presenza di masse incurva lo spazio-tempo, ed è responsabile, in determinate situazioni, del moto dei corpi. Ad esempio, questa formulazione rappresenta un nuovo modo di considerare l’attrazione tra due corpi che era stata spiegata con la forma di attrazione gravitazionale.

Come sappiamo dalla fisica classica, due corpi che possiedono una massa sono attratti tra loro da una forza direttamente proporzionale alle masse e inversamente proporzionale al quadrato della distanza. Secondo la relatività generale, invece, tale forza non esiste.

Einstein affermò che la presenza di una massa incurva lo spazio in cui essa si trova, e tale deformazione è responsabile dell’avvicinamento delle due masse. Lo spazio-tempo presenta deformazioni più accentuate nelle zone più vicine alle masse, rispetto a quelle più lontane.

Esempio del telo elastico

Questo concetto può essere facilmente rappresentato per mezzo di un esempio classico; consideriamo una massa che viene posta al centro di un telo elastico; notiamo che la massa, a causa del suo peso, crea una deformazione del telo.

Supponiamo, ora, di posizionare una massa molto più piccola sul bordo del telo; anche la seconda massa è responsabile di una piccola deformazione del telo nella zona circostante, ma questa risulta trascurabile rispetto a quella della massa più grande.

Inoltre, la massa piccola tende a scivolare verso quella più grande, come se fosse attratta da essa.

curvatura-spazio-tempo

Possiamo immaginare una situazione analoga per i pianeti che su muovono attorno al sole, e per la luna che orbita attorno alla Terra.

I corpi soggetti alla forza di gravità si muovono nello spazio curvo come particelle libere

Il secondo concetto che fu introdotto da Einstein è che i corpi soggetti alla forza di gravità si muovono nello spazio curvo come particelle libere, seguendo linee di minima lunghezza che congiungono due punti distinti; tali linee vengono definite geodetiche.

In uno spazio piano, le curve geodetiche sono costituite da segmenti di retta, perché come sappiamo, il cammino più breve che congiunge due punti in un piano è il segmento che li unisce.

In uno spazio curvo, però, tali curve assumono un significato differente. Per prima cosa, dobbiamo definire il concetto di retta in uno spazio curvo: si definisce una retta passante per due punti una linea rappresentata dalla circonferenza massima , cioè l’intersezione della sfera con un piano passante per il centro di essa.

In questo modo, un segmento di tale curva rappresenta il cammino minimo che congiunge i due punti.

Quando due masse si attraggono per effetto della curvatura dello spazio, esse si muovono l’una verso l’altra come se seguissero tali segmenti di retta, cioè percorrendo le geodetiche.

Esempio della superficie sferica

Consideriamo, ad esempio, due masse di uguali dimensione, che generano nello spazio-tempo la stessa deformazione; supponiamo che nello stesso spazio sia presente anche una terza massa, molto più grande delle precedenti, che genera quindi una deformazione dello spazio-tempo molto più rilevante. Le due masse piccole, quindi, sono attratte in modo uguale verso la massa più grande, per effetto della deformazione creata da quest’ultima.

Rappresentiamo la stessa situazione in un contesto diverso, in cui può essere messo bene in evidenza il percorso seguito dalle masse.

Ipotizziamo che la massa più grande si trovi sulla sommità di una sfera, e le due masse più piccole sulla sua superficie;

curvatura-spazio-tempo

La deformazione dello spazio fa si che le masse minori si avvicinino a quella più grande seguendo due archi di circonferenza massima; questi si ottengono a partire da due circonferenze massime passanti per la posizione iniziale delle singole masse piccole, e per la sommità della sfera.

Potrebbero Interessarti

Video Lezioni: Relatività

La deflessione gravitazionale della luce

Come abbiamo già visto, una delle conseguenze del principio di relatività generale, secondo il quale le leggi della fisica hanno la stessa forma in tutti i sistemi di riferimento, è il fatto che non è più valido l’assioma sulla costanza della luce; infatti, se osserviamo un raggio di luce emesso da un sistema di riferimento accelerato, e quindi non inerziale, notiamo che il raggio non si propaga in linea retta, ma subisce una deviazione.

Secondo il principio di equivalenza, inoltre, sappiamo che gli stessi effetti prodotti dalle forze presenti in un campo gravitazionale possono essere riscontrati in un sistema accelerato; viene, quindi, spontaneo chiedersi se anche in un campo gravitazionale possa essere presente il fenomeno della deviazione della luce.

La deflessione della luce

La deflessione della luce è un fenomeno particolarmente difficile da osservare, e presenta effetti maggiori nel caso di un campo gravitazionale particolarmente intenso; nel nostro caso, gli effetti della deviazione dei raggi luminosi sono studiati in presenza del campo gravitazionale generato dal Sole.

In presenza di una grande massa, infatti, i raggi di luce proveniente dalle stelle possono subire delle deflessioni rispetto ai raggi che si propagano in linea retta; di conseguenza, se dalla Terra si osserva una stella la cui luce è stata deflessa dalla presenza del Sole, tale stella apparirà in una posizione leggermente diversa rispetto a quella reale.

deflessione della luce: posizione apparente di una stella

Fenomeno delle lenti gravitazionali

Uno degli effetti più rilevanti della deflessione della luce è il fenomeno delle lenti gravitazionali. Tale fenomeno si manifesta quando tra una sorgente luminosa, ad esempio un quasar (cioè una galassia lontanissima dalla Terra, dalla quale proviene un’intensa emissione radio), e la Terra si interpone una galassia.

La galassia che si trova sulla congiungente Terra-quasar funge come da lente per i raggi che vengono emessi dal quasar, che quindi risultano leggermente deviati. La deviazione di tali radiazioni fa si che dalla Terra non si osservi semplicemente un oggetto, ma risultano visibili due immagini dell’oggetto che si trovano in punti speculari rispetto alla posizione originale.

Lente gravitazionale

La presenza di un forte campo gravitazionale, inoltre, è responsabile anche di altri fenomeni; abbiamo visto in precedenza che, per l’effetto doppler relativistico, le onde emesse da una sorgente luminosa vengono percepite da un’osservatore sulla Terra con una frequenza minore di quella con cui vengono emesse.

Si parla quindi di redshift gravitazionale, o spostamento verso il rosso, in quanto le lunghezze d’onda delle onde emesse risultano spostate nello spettro verso l’estremo di colore rosso.

Il campo gravitazionale e il tempo

Se considerassimo un’onda elettromagnetica come un orologio, potremmo dire che, a causa del campo gravitazionale, il tempo rilevato da un osservatore sulla Terra è differente da quello misurato dall’orologio.

In particolare, si può affermare che gli orologi che si trovano in presenza di un campo gravitazionale maggiore risultano procedere più lentamente rispetto a quelli che si trovano in zone dello spazio-tempo in cui la curvatura è meno accentuata (in queste zone il campo gravitazionale è minore).

Possiamo descrivere questo fenomeno anche affermando che per orologi che si trovano vicini a corpi particolarmente massivi il tempo scorre più lentamente rispetto ad orologi che invece ne sono lontani. Il fenomeno prende il nome di dilatazione gravitazionale dei tempi.

E’ proprio su questi fenomeni che si basa una delle verifiche moderne della teoria della relatività generale; tale verifica consiste nel calcolare il tempo di percorrenza del viaggio di andata e ritorno di un fotone, passando da un pianeta ad un altro, quando la sua traiettoria passa in prossimità del Sole (quando i due pianeti in questione sono eclissati dal Sole).

A causa della curvatura del percorso del fotone, e della dilatazione gravitazionale dei tempi, si misura un tempo di percorrenza differente rispetto a un cammino rettilineo della particella.

Potrebbero Interessarti

Video Lezioni: Relatività

La carica elettrica e l’elettrizzazione per strofinio

La carica elettrica

La carica elettrica è una grandezza fisica che misura la capacità dei corpi di di elettrizzarsi, cioè di acquisire la capacità di attrarre a sé altri oggetti.

Nel corso dei primi studi che vennero effettuati sulle cariche elettriche, si notò che era possibile elettrizzare un corpo mediante strofinio; si individuarono, così, due tipi di cariche elettriche:

venne definita carica elettrica positiva quella dei corpi che si comportavano come il vetro;

si definì, invece, carica elettrica negativa quella dei corpi che avevano lo stesso comportamento della plastica.

Tramite esperimenti pratici, quindi, si notò che le cariche elettriche che possiedono lo stesso segno, una volta elettrizzate, si respingono, mentre cariche elettriche di segno opposto si attraggono.

Elettrizzazione di un corpo

Infatti, elettrizzando due barrette di plastica e avvicinandole tra loro, si può notare che queste tendono ad allontanarsi; invece avvicinando una barretta di plastica ad una di vetro, entrambe elettrizzate, si nota che esse tendono ad unirsi.

elettrizzazione

Questo fenomeno può essere spiegato attraverso un modello microscopico, cioè considerando le cariche positive e negative dei corpi che interagiscono tra loro.

Come sappiamo, la materia è costituita da molecole, che a loro volta sono formate da atomi, costituiti da elettroni, neutroni e protoni. Gli elettroni hanno carica negativa, i protoni carica positiva e i neutroni sono privi di carica elettrica.

All’interno di un atomo il numero di elettroni è uguale al numero di protoni, e quindi l’atomo, in condizioni normali, è neutro.

Un corpo elettricamente carico, quindi, è un corpo che presenta uno squilibrio tra il numero di elettroni e il numero di protoni; tale squilibrio di carica è dovuto allo spostamento di elettroni da un corpo ad un altro.

Infatti, in un atomo, i protoni sono legati tra loro e insieme ai neutroni; questa aggregazione forma un complesso che viene definito nucleo. Gli elettroni, invece, possono orbitare attorno al nucleo, e sono quindi liberi di muoversi.

Un corpo carico positivamente, quindi, è un corpo che presenta un eccesso di protoni, e che quindi ha perso degli elettroni; al contrario, un corpo carico negativamente è un corpo che ha un numero di elettroni in eccesso, e che quindi ha acquistato elettroni da un altro corpo.

Elettrizzazione per strofinio

L’elettrizzazione per strofinio comporta il passaggio di elettroni da un corpo ad un altro, cosicché uno di essi si caricherà positivamente, mentre l’altro negativamente.

E’ proprio l’energia cinetica che si genera quando due corpi vengono strofinati velocemente induce il passaggio degli elettroni.

Ad esempio, se strofiniamo con un panno di lana una barretta di vetro, vi sarà un passaggio di elettroni dal vetro alla lana, e quindi la barretta di vetro, che ha perso elettroni, acquisterà carica positiva.

Il numero totale di cariche della sbarretta e del panno fa si che, nel complesso, i due corpi risultino neutri; cioè, il numero di elettroni persi dalla sbarretta di vetro è esattamente uguale al numero di elettroni acquistati dal panno.

L’elettrizzazione per strofinio avviene solo per determinati oggetti, fra cui appunto quelli in vetro e i materiali plastici. Questi oggetti, infatti, hanno la caratteristica di poter trattenere le cariche nella zona in cui sono state trasferite; le cariche, quindi, non sono libere di muoversi all’interno del corpo.

Gli oggetti metallici, invece, non possono essere elettrizzati per strofinio; se provassimo, infatti, a strofinare con un panno di lana una barretta di metallo, vi sarebbe anche in questo caso un passaggio di cariche dovuto all’energia cinetica dello sfregamento.

Tuttavia i metalli godono di una particolare caratteristica: in essi gli elettroni sono liberi di muoversi sulla superficie del corpo, e possono passare nella nostra mano, e all’interno del nostro corpo, fino a scaricarsi a terra. La barretta, quindi, ritornerebbe ad essere neutra.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: L’elettrizzazione per induzione

Appunti: L’elettrizzazione per contatto

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

L’elettrizzazione per contatto

Conduttori e isolanti

Abbiamo visto precedentemente che uno dei modi per elettrizzare un corpo è quello di strofinarlo con un panno di lana; in questo modo si genera un passaggio di cariche tra un corpo e l’altro, e essi risultano elettricamente carichi.

Tuttavia, questo metodo non funziona con tutti i corpi, ma solo quelli fatti con determinati materiali.

Nel caso di metalli, infatti, l’elettrizzazione per contatto non è efficace, perché nei metalli gli elettroni sono liberi di muoversi sulla superficie del corpo; essi, quindi, possono quindi passare nella nostra mano, e attraverso il nostro corpo scaricarsi a terra.

Potremmo elettrizzare un metallo per strofinio solo nel caso in cui il corpo avesse un manico di plastica; in questo caso, la plastica impedirebbe alle cariche elettriche di passare nel nostro corpo, e quindi esse rimarrebbero sulla superficie del metallo.

Questa particolare proprietà permette di classificare i materiali in due importanti categorie:

i conduttori sono sostanze come i metalli, o il corpo umano, tali per cui gli elettroni possono muoversi liberamente all’interno di essi;

gli isolanti sono materiali come la plastica e il vetro; la loro caratteristica sta nel fatto che possono essere elettrizzati per strofinio, in quanto le cariche elettriche tendono a rimanere nella posizione originale, e non sono libere di muoversi sulla superficie del corpo.

Elettrizzazione per contatto

Come abbiamo visto, gli isolanti possono facilmente essere elettrizzati per strofinio, mentre questo metodo non funziona con i conduttori.

Anche i conduttori, però, possono essere elettrizzati, e il tipo di elettrizzazione efficace nel loro caso è quella per contatto.

Questo metodo consiste nell’avvicinare un conduttore carico elettricamente (con un eccesso di elettroni) ad uno neutro; quando i due conduttori vengono portati a contatto, una parte della carica presente sul primo viene trasferita al secondo, cosicché anch’esso risulti carico. In questo modo, entrambi i conduttori risulteranno elettricamente carichi.

elettrizzazione-per-contatto

In particolare, la carica si distribuisce equamente tra i due conduttori, in modo che essi abbiano lo stesso numero di particelle negative. L’elettrizzazione per contatto fa si che i corpi continuino a rimanere carichi anche dopo l’allontanamento; la carica presente su di essi, quindi, è permanente.

L’elettroscopio

L’elettrizzazione per contatto viene adoperata in un particolare strumento, detto elettroscopio, per misurare operativamente la carica elettrica.

Questo strumento è costituito da un recipiente di vetro che presenta sulla sommità un pomello metallico; da tale pomello parte un’attinica metallica contenuta all’interno del contenitore, che presenta all’estremità due lamine conduttrici molto sottili chiamate “foglie”.

La misurazione della carica elettrica avviene avvicinando un corpo elettricamente carico (ad esempio una sbarretta metallica elettrizzata) al pomello metallico; quando si raggiunge il contatto tra il pomello e la sbarretta, la carica elettrica si distribuisce uniformemente all’interno dei due conduttori, e dal pomello può scorrere lungo l’asta verticale fino a raggiungere le foglie.

Le foglioline, che risultano cariche dello stesso segno, tendono a respingersi, e quindi ad allargarsi; misurando il grado di aperture delle foglioline, è possibile ottenere una misura operativa della carica elettrica presente sulla sbarretta metallica.

elettroscopio-a-foglie — Elettroscopio a foglie.

Con questo metodo è possibile anche confrontare due oggetti elettrizzati per stabilire quali di essi possiede una carica maggiore.

Si può procedere misurando l’aperture delle foglie relative a ciascun corpo; se la misura risulta essere la stessa in entrambi i casi, si conclude che i due corpi possiedono la stessa carica; in caso contrario quello che determina un’aperture maggiore delle foglioline è quello che ha carica maggiore.

Notiamo che, una volta avvenuto il contatto tra il primo corpo e il pomello, la carica presente sul corpo si distribuisce uniformemente tra i due oggetti.

La carica, quindi, rimane sul pomello e si diffonde sull’asta verticale fino a raggiungere le foglioline, e tende a rimanerci anche dopo il contatto. Se avvicinassimo al pomello il secondo corpo, non otterremmo una corretta misura della sua carica; infatti sul pomello era rimasta anche la carica proveniente dal primo.

E’ necessario, quindi, scaricare il pomello, cioè farlo tornare neutro, prima di procedere con la seconda misurazione.

Per farlo è sufficiente toccare il pomello con la mano, cosicché le cariche elettriche, passando attraverso il nostro corpo, si scarichino a terra.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: L’elettrizzazione per strofinio

Appunti: L’elettrizzazione per induzione

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

La legge di Coulomb

la definizione di Coulomb

Come abbiamo visto precedentemente, è possibile dare una misura operativa della carica elettrica di un corpo attraverso uno strumento chiamato elettroscopio.

Tale misurazione dipende dall’aperture delle foglioline metalliche dello strumento in seguito al contatto del pomello conduttore con una barretta metallica.

Per misurare la carica, quindi, è necessario scegliere una carica come unità di misura, e poi porre una scala graduata al di sotto delle foglioline per misurare la loro apertura.

Nel Sistema Internazionale, si misura la carica elettrica di un corpo in Coulomb, dal nome del fisico francese Charles Augustin Coulomb. La definizione di questa unità di misura parte dalla carica elettrica più piccola che si trova in natura, cioè quella dell’elettrone.

La carica dell’elettrone, indicata con e, vale:

$ e = 1,6022 * 10^(-19) C $

Poiché l’elettrone è la carica elettrica più piccola mai misurata, essa vien definita carica elementare, e tutte le altre particelle e cariche elettriche presenti in natura possiedono una carica che è multiplo di quella dell’elettrone.

Per la carica elettrica esiste una legge analoga a quella della conservazione dell’energia e della materia; abbiamo visto, infatti, che quando elettrizziamo un corpo per strofinio, vi è un passaggio di cariche da un corpo ad un altro, ma gli elettroni acquistati dal corpo negativo sono, in numero, pari a quelli persi dal corpo positivo.

In generale, quindi, possiamo affermare che anche la carica elettrica si conserva, e la quantità di carica elettrica totale rimane invariata nel tempo, anche in seguito a scambi di cariche per elettrizzazione.

La legge di Coulomb

Quando un corpo elettricamente carico viene avvicinato ad un corpo carico dello stesso segno, i due corpi tendono a respingersi; quando, invece, i corpi sono carichi con segni opposti, essi si attraggono.

Anche fra i corpi carichi, quindi, esiste una forza a distanza responsabile dell’attrazione o della repulsione tra essi.

Tale forza prende il nome di forza di Coulomb è una grandezza vettoriale; nella sua definizione, quindi, dobbiamo includere informazioni riguardanti direzione, verso e modulo.

La direzione della forza è data dalla retta congiungente le cariche elettriche, mentre il suo verso dipende dal loro segno: la forza sarà attrattiva se le cariche hanno segno opposto, mentre sarà repulsiva se le cariche hanno lo stesso segno.

legge-di-coulomb — Le cariche opposte si attraggono, mentre quelle dello stesso segno si respingono.

Il modulo di questa forza è direttamente proporzionale alle cariche dei corpi, e inversamente proporzionale al quadrato della loro distanza:

$ F = k_0 * frac(Q_1 * Q_2)(r^2) $

La costante k, determinata sperimentalmente, vale:

$k_0 = 8,99 * 10^9 frac(N * m^2)(C^2) $

Questa costante può anche essere espressa come:

$k = frac(1)(4πε_0)$

dove la costante che compare al denominatore prende il nome di costante dielettrica assoluta del vuoto, e vale:

$ ε_0 = 8,854 * 10^(-12) frac(C^2)(N * m^2) $

In funzione di tale costante, quindi, possiamo esprimere la forza di Coulomb nel vuoto con la seguente formula:

$ F = frac(1)(4πε_0) * frac(Q_1 * Q_2)(r^2) $

Se, però, due oggetti elettricamente carichi sono posti all’interno di un mezzo, ad esempio in acqua, la forza di Coulomb con cui le cariche si attraggono o respingono sarebbe minore di quella che agisce nel vuoto.

L’espressione del modulo della nuova forza è dato da:

$ F = frac(F)(ε_r) = frac(k_0)(ε_r) * frac(Q_1 * Q_2)(r^2) $

La costante dielettrica relativa dipende dal mezzo che stiamo considerando, ed è un numero puro.

Analogie con la forza gravitazionale

Possiamo notare molte analogie della forza di Coulomb con la forza gravitazionale, sia per la somiglianza della formula che esprime il suo modulo, sia per la tipologia di forza.

Entrambe le forze, infatti, sono forze a distanza, e il loro modulo è direttamente proporzionale alla proprietà caratteristica dei corpi (cioè ,alle masse in un caso, e alle cariche nell’altro), e inversamente proporzionale al quadrato della loro distanza; inoltre, in entrambi i casi il modulo dipende anche da una costante.

Tuttavia, tra le due forze sussistono anche importanti differenze.

Mentre la forza elettrica è sia attrattiva che repulsiva, quella gravitazionale è solo attrattiva; inoltre, la forza elettrica è molto più intensa di quella gravitazionale, anche per il fatto che la costante k0 presenta un fattore $10^9$, mentre la costante di Cavendish un fattore $10^(-11)$ .

Mentre, però, la forza gravitazionale agisce tra qualunque corpo sia dotato di massa, la forza elettrica agisce solamente tra corpi carichi elettricamente.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: L’elettrizzazione per strofinio

Appunti: L’elettrizzazione per contatto

Appunti: L’elettrizzazione per induzione

Appunti: Il campo elettrico

Appunti: Le linee di campo

L’elettrizzazione per induzione

L’elettrizzazione per induzione consiste nell’avvicinare un corpo elettricamente carico ad un corpo neutro, se quest’ultimo è un conduttore.

Ad esempio, se proviamo ad avvicinare una bacchetta elettricamente carica ad una sfera metallica neutra, notiamo che la sfera verrà attratta verso la barretta, anche se la sfera inizialmente è neutra.

elettrizzazione-per-induzione

Questo fenomeno può essere spiegato considerando il fatto che la sferetta che viene attratta è un corpo metallico, e quindi conduttore. In questo caso, infatti, sappiamo che le particelle sono libere di muoversi sulla superficie della sfera.

Mentre inizialmente la sfera è neutra, e quindi le particelle positive e negative si trovano sparse uniformemente su di essa, quando avviciniamo la barretta, che supponiamo essere carica negativamente, si ha una redistribuzione di cariche sulla superficie della sfera.

Poiché le cariche dello stesso segno si attraggono, mentre quelle di segno opposto i respingono, sulla parte della sfera più vicina alla bacchetta si concentreranno le cariche positive, mentre quelle negative si posizioneranno più lontano possibile da essa.

In questo modo nella sfera metallica, nonostante essa sia nel complesso ancora neutra, si ha una nuova distribuzione di carica.

L’induzione elettrostatica, però, permette un’elettrizzazione solo temporanea di un corpo; infatti, quando allontaniamo la bacchetta dalla sfera, non essendoci più l’influsso delle cariche negative ad alterare l’equilibrio elettrostatico del corpo, nella sfera le cariche positive tornano a mescolarsi con quelle negative, e la sfera torna ad essere neutra come in partenza, con una distribuzione uniforme di cariche.

E’ possibile, però, rendere l’induzione elettrostatica permanente; per farlo, occorre eliminare le cariche elettriche negative che sono localizzate nella semisfera lontana dalla bacchetta; possiamo, ad esempio, toccare con un dito la sfera, cosicché le cariche negative vengano scaricate a terra.

elettrizzazione-per-induzione

L’elettroforo di Volta

L’elettroforo di Volta rappresenta uno strumento che, attraverso l’induzione elettrostatica, è in grado di accumulare e separare cariche elettriche.

Lo strumento è composto da uno strato di resina (o un materiale isolante) e da un disco metallico dotato di manico isolante.

Il suo funzionamento prevede l’elettrizzazione tramite strofinio dello strato di resina, che si carica così negativamente. Poi si pone il disco metallico a contatto con lo strato di resina: in questo modo la parte del disco a contatto con la resina si carica di segno positivo, mentre quella più distante di segno negativo.

Successivamente, toccando con un dito il disco metallico si scaricano a terra le cariche negative, e il disco rimane positivamente carico.

elettroforo-di-volta — Elettrizzazione permanente con l’elettroforo di Volta.

La polarizzazione

Anche nel caso degli isolanti la vicinanza di un corpo carico elettricamente ad un corpo neutro influisce nella disposizione delle cariche.

Sappiamo, però, che nel caso degli isolanti gli elettroni non sono liberi di muoversi all’interno del corpo; tutte le particelle, quindi, rimangono nella loro posizione.

Tuttavia, gli elettroni possono comunque spostarsi all’interno delle molecole, che così si orientano dando luogo ad una piccola ridistribuzione di cariche.

Questo fatto spiega, ad esempio, come mai se elettrizziamo una bacchetta di plastica strofinandola con un panno di lana, sia poi possibile attrarre con essa dei leggeri pezzetti di carta.

La bacchetta di plastica, infatti, si carica negativamente, e le molecole che costituiscono ogni frammento di carta subiscono una redistribuzione di carica.

In questo modo in ognuna di esse le cariche positive si verranno a trovare nella zona della molecola più vicina alla bacchetta; quelle negative, invece, si spostano dalla parte opposta, perché vengono respinte.

La polarizzazione avviene anche quando le cariche elettriche si trovano all’interno di un mezzo. Abbiamo visto che in questo caso la forza attrattiva fra due cariche è minore rispetto a quella che si avrebbe nel vuoto.

Infatti, all’interno di un mezzo la presenza di una carica elettrica fa si che le molecole di tale mezzo si polarizzino, circondando la carica in questione.

La carica, quindi, risulta schermata dalle molecole circostanti, e la forza con cui essa può interagire con altre cariche elettriche risulta assai diminuita.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: L’elettrizzazione per strofinio

Appunti: L’elettrizzazione per contatto

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

Il campo elettrico

Una spiegazione alternativa per l’attrazione tra corpi carichi

Come abbiamo visto in precedenza, esiste una forza, detta forza di Coulomb, responsabile dell’attrazione tra cariche elettriche di segni opposti; tale forza è una forza a distanza, come la forza di attrazione gravitazionale.

In un primo momento, quindi, si pensava l’interazione tra corpi carichi solo come effetto della forza di Coulomb.

Intorno alla metà dell’ottocento, però, fu introdotto un nuovo punto di vista sul fenomeno, ad opera dello scienziato inglese Michael Faraday. Egli spiegò il fenomeno dell’interazione tra corpi carichi con il concetto di campo elettrostatico.

Egli affermò che anche una singola carica elettrica è in grado di generare un campo elettrico, indipendentemente dal fatto che sia presente o meno una seconda carica con cui essa interagisca.

Anche in questa nuova interpretazione, pero, la forza di Coulomb continua ad agire.

Consideriamo una carica $Q_1$ ; la sua presenza nello spazio modifica lo spazio circostante, cosicché le proprietà di ogni punto di esso vengono modificate.

Se in tale spazio è presente una carica $Q_2$ , essa risente ella modifica dello spazio in cui si trova avvertendo una forza elettrica, quella di Coulomb.

Campo elettrico e telo elastico

Per capire meglio il concetto di campo elettrico, ipotizziamo che lo spazio possa essere rappresentato con un telo elastico, e la carica con una sfera.

Supponiamo che una carica Q si trovi nello spazio; nel nostro modello, se poniamo una sfera sopra un telo elastico, notiamo che esso si piega e si deforma sotto il suo peso; possiamo dire che la carica ha modificato lo stato di tensione dello spazio.

Prendiamo, ora, una seconda carica q, molto più piccola della precedente, detta carica esploratrice, in quanto il modo in cui essa modifica lo spazio è trascurabile rispetto all’altra.

Se poniamo la carica q all’interno dello spazio che era già stato modificato da Q, essa risente di tale deformazione, e viene attratta verso la carica generatrice.

Possiamo immaginare questo fatto osservando cosa accade se poniamo una sfera di piccole dimensioni ai lati del telo deformato: la pallina tende a scivolare nella direzione della massa più grande.

La carica di prova q è attratta dalla carica generatrice Q perché sottoposta alla forza di Coulomb.

Definizione del vettore campo elettrico

Ricordiamo che la forza che lega le due cariche è una grandezza vettoriale, ed è data dalla seguente espressione:

$vec F = k_0 * frac(Q*q)(r^2) * vec u$

Dove il vettore $ vec u$ è un vettore unitario, che giace sulla retta congiungente le due cariche, e verso che dipende dal segno di esse.

Come detto in precedenza, dalle supposizioni di Faraday il campo elettrico sussiste anche in assenza della seconda carica, quella di prova; di conseguenza, possiamo definire il vettore campo elettrico in questo modo:

$vec E = frac(vec F)(q) = k_0 * frac(Q)(r^2) * vec u $

Il vettore campo elettrico ha stessa direzione del vettore forza; il suo verso, invece, dipende dal segno della carica di prova: se la carica q ha segno positivo, allora il vettore campo elettrico e il vettore forza hanno lo stesso verso, altrimenti hanno verso opposto.

Come sappiamo, all’interno di un mezzo, come l’acqua per esempio, il valore della forza elettrica è minore di quello che si avrebbe nel vuoto, in quanto le particelle del mezzo tendono a schermare la carica in questione.

Anche il modulo del campo elettrico, quindi, varia, e rispetto a quello nel vuoto risulta diviso per un fattore 4πε:

$ E_m = frac(F_m)(q) =frac(k_0)(ε_r) * frac(Q)(r^2) $

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: La legge di Coulomb

Appunti: Le linee di campo

Le linee di campo

Rappresentazione del campo elettrico mediante le linee di campo

Il campo elettrico, come abbiamo visto, è una grandezza vettoriale; in quanto tale, le caratteristiche che la descrivono sono modulo, direzione e verso.

Nell’espressione del vettore campo elettrico non compare la carica di prova; di conseguenza il campo elettrico rappresenta una grandezza vettoriale che non dipende dalla carica di prova, ma solo dalla carica generatrice.

I vettori campo elettrico hanno direzione radiale rispetto alla carica generatrice. Il verso del vettore dipende dal segno della carica; se questa è positiva il verso è uscente; se, invece, Q è negativa i vettori campo elettrico hanno verso entrante.

Il campo elettrico, quindi, può essere facilmente considerato attraverso questa rappresentazione; poiché la direzione dei vettori campo elettrico è radiale rispetto alla carica generatrice, si visualizza il campo elettrico proprio attraverso delle linee che seguono la direzione di tali vettori; le linee prendono il nome di linee di campo.

Nel caso di una carica puntiforme che genera il campo elettrico, le linee di campo sono costituite da semirette originate nel punto in cui si trova la carica generatrice.

Nel caso di una carica positiva, le linee di campo escono da essa, e i vettori campo elettrico hanno verso uscente.

Altrimenti, le linee di campo entrano nella carica negativa, e i vettori campo elettrico hanno verso anch’essi entrante.

Rappresentazione delle linee di campo: un caso pratico

Nella realtà queste linee non esistono; però, per avere un’idea del campo elettrico generato da una carica, possiamo immaginare una situazione analoga considerando il campo magnetico: se prendiamo un foglio di carta, lo cospargiamo con della limatura di ferro, e poniamo sotto di esso una calamita, vedremo una situazione come questa:

La stessa situazione si verifica nel caso di una carica puntiforme, che da luogo ad un campo ad andamento radiale; le linee di forza, infatti, sono disposte a raggiera intorno alla carica.

Notiamo che le linee di campo sono più fitte in vicinanza della carica elettrica, e la loro densità diventa minore mano a mano che ci si allontana da essa.

Il campo elettrico, infatti, è più intenso in prossimità della carica generatrice, in quanto il suo modulo è inversamente proporzionale al quadrato della distanza tra essa e un ipotetica carica di prova.

Possiamo dire, quindi, che la densità delle linee di campo è direttamente proporzionale all’intensità del campo elettrico.

Linee di campo elettrico generato da due cariche

Possiamo visualizzare le linee di campo anche nel caso in cui siano presenti non una ma due cariche, che creano un campo elettrico.

Esaminiamo il caso in cui le cariche abbiano segni opposti; in questo caso, le cariche si attraggono, quindi nello spazio che separa le due cariche, i campi generati da esse si rafforzano. Se ponessimo una carica di prova positiva in quello spazio, essa verrebbe respinta dalla carica $Q_1$ positiva, e attratta dalla carica $Q_2$ negativa.

Possiamo rappresentare, quindi, le linee di campo in questo modo:

Nel caso in cui, invece, le cariche abbiano lo stesso segno, nella zona che le separa, i campi elettrici tendono ad annullarsi; se ponessimo una carica q positiva all’interno di tale spazio, infatti, essa verrebbe respinta da entrambe le cariche generatrici.

La rappresentazione delle linee di campo in questa situazione è la seguente:

Notiamo che ai lati delle cariche, in entrambe le situazioni, le linee di campo sono simili a quelle che si hanno nel caso di una sola carica puntiforme; infatti in quelle zone l’influsso dell’altra carica è talmente piccolo che può essere trascurato.

Linee di campo elettrico in un condensatore

Un’ ulteriore configurazione di campo elettrico è quella data dal campo elettrico uniforme, cioè un campo elettrico il cui modulo è uguale in ogni punto.

Per generare un campo elettrico di questo tipo, si utilizzano delle piastre cariche di segno opposto (condensatore); in questo caso, il campo elettrico presenta linee di campo che sono parallele tra loro, e hanno densità costante. Il verso dei vettori campo elettrico va dalla piastra positiva a quella negativa:

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Il flusso del campo elettrico

Per capire il concetto di campo elettrico dobbiamo introdurre quello di campo vettoriale.

Un campo vettoriale è una legge matematica che associa ad ogni punto del piano, o dello spazio, un vettore.

Sappiamo che la presenza di una carica elettrica nello spazio genera un campo elettrico; ciò significa che in ogni punto dello spazio è possibile individuare un vettore campo elettrico che esprima l’intensità del campo in quel punto.

Se nello spazio fossero presenti un numero n di cariche elettriche, il campo elettrico risultante sarà quello generato dalla somma dei campi elettrici generati da ciascuna carica. Supponiamo che tale campo elettrico sia uniforme, cioè che il vettore campo elettrico sia lo stesso in ogni punto per modulo, direzione e verso.

Il flusso del campo elettrico attraverso una superficie

Se consideriamo una superficie piana di area S, possiamo introdurre una nuova grandezza scalare, il flusso del campo elettrico attraverso la superficie S:

$Φ_(vec S) (vecE) = vec E * vec S $

Il vettore S è un vettore superficie: la sua direzione è perpendicolare alla superficie considerata, il suo verso è, per convenzione, uscente dalla superficie (nel caso di una superficie chiusa), mentre il suo modulo è pari all’area della superficie stessa.

Dalla definizione, essendo il flusso del campo vettoriale un prodotto scalare, possiamo individuare situazioni particolari in cui il flusso è massimo o minimo.

Svolgendo il prodotto scalare, otteniamo la seguente formula:

$Φ_(vec S) (vecE) = vec E * vec S = E * S * cos α $

dove α indica l’angolo formato dal vettore campo elettrico e il vettore superficie.

flusso-del-campo-magnetico — Il vettore normale della superficie considerata può formare un angolo nullo con il campo magnetico o un angolo $\alpha$

Di conseguenza, possiamo affermare che il flusso del campo elettrico è massimo quando l’angolo è di 0° o di 180°; in questo caso il vettore campo elettrico e il vettore superficie sono paralleli (in questo caso, la superficie è perpendicolare alle linee di campo).

Il flusso del campo, invece, è nullo quando il vettore campo elettrico è perpendicolare alle linee di campo; in questo caso, le linee di campo sono parallele e radenti alla superficie.

Possiamo estendere il concetto di flusso del campo elettrico anche a superfici che non sono piane; si procede suddividendo la superficie in n parti, costruendo un reticolo, in modo che ciascun quadratino del reticolo rappresenti una piccola superficie piana, che rispetti le condizioni della definizione di flusso.

Su ognuna di esse si calcola il flusso del campo elettrico, e la somma dei flussi calcolati su ciascuna superficie fornisce il valore del flusso sull’intera distribuzione.

Se indichiamo con $E_i$ il campo elettrico relativo alla superficie i-esima $∆S_i$ , il flusso complessivo del campo elettrico attraverso la superficie S è dato dalla seguente formula:

$Φ_(vec S) (vecE) = \sum_{i=1}^n Φ_i (vecE) = \sum_{i=1}^n (vec E_i * ∆vec S_i) $

Il teorema di Gauss

Il teorema di Gauss per il campo elettrico afferma che il flusso del campo elettrico su una superficie chiusa è direttamente proporzionale alla carica totale che si trova all’interno della superficie.

In questo caso, il flusso del campo elettrico è descritto dalla seguente relazione:

$ Φ_Ω (vec E) = frac(Q_(Tot))(ε) $

Dove Ω indica la superficie chiusa, mentre ε e una costante, la costante dielettrica del mezzo.

Notiamo che il flusso del campo elettrico attraverso una superficie chiusa è indipendente dalla grandezza e dalla forma della superficie, e dal numero delle cariche presenti all’interno di essa.

La dimostrazione di questo teorema prevede alcune considerazioni particolari; si suppone che la superficie considerata sia sferica, di raggio r, e che la carica generatrice sia una sola, posizionate nel centro della sfera.

Si suddivide la sfera in un reticolo, e si indica ciascuna superficie individuata con $∆S_i$ ; tutti i vettori superficie sono uscenti dalla sfera, e hanno direzione radiale; in ogni punto della sfera il vettore campo elettrico è uscente dalla sfera, e ha anch’esso direzione radiale.

teorema-di-Gauss — Dimostrazione del teorema di Gauss utilizzando una sfera come superficie chiusa.

Si procede determinando il flusso del campo vettoriale in ogni superficie infinitesima, che sappiamo essere:

$Φ_i (vecE) = vec E_i * ∆vec S_i = E_i * ∆S_i $

Sappiamo anche che il modulo del vettore campo elettrico è dato dal rapporto della forza elettrica sulla carica di prova; esso, quindi, può essere scritto come:

$ E_i = frac(1)(4πε) * frac(Q)(r^2) $

dove ε è la costante dielettrica del mezzo. I vettori campo elettrico, quindi, hanno tutti lo stesso modulo, in quanto la superficie è equidistante in ogni punto dalla carica generatrice.

Possiamo quindi determinare il flusso del campo elettrico totale come somma dei flussi nelle singole superfici:

$ Φ_Ω (vec E) = E_1 * ∆S_1 + …. + E_n * ∆S_n = $

$E * (∆S_1 + ….. + ∆S_n) = E * S_Ω$

La somma di tutte le superfici che costituiscono il reticolo da la superficie totale della sfera, che sappiamo essere $4πr^2$.

La formula del teorema di Gauss è quindi dimostrata:

$ Φ_Ω (vec E) =E * S_Ω = frac(1)(4πε) * frac(Q)(r^2) * 4πr^2 = frac(Q)(ε)$

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

Campi elettrici con particolari simmetrie

Vediamo alcuni esempi di particolari campi elettrici che presentano delle simmetrie.

La distribuzione piana infinita di carica

Ipotizziamo di poter creare un piano infinito, che presenti una carica uniforme in ogni suo punto; se il piano è immerso in un mezzo con costante dielettrica ε, possiamo dimostrare che il modulo del campo elettrico è dato dalla seguente formula:

$ E = frac(σ)(2ε)$

dove σ è la densità superficiale di carica, data dal rapporto tra la carica ∆Q e l’area ∆S sella superficie.

La direzione del vettore è perpendicolare al piano, mentre il verso dipende dal segno della carica: sarà entrante nel piano in caso di carica negativa, e uscente nel caso di carica positiva.

In tutti i punti esterni al piano ci carica, quindi, il vettore campo elettrico è perpendicolare al piano, ed è lo stesso in tutti i punti che hanno stessa distanza dal piano.

Notiamo, inoltre, che il verso del vettore cambia in base alla parte in cui ci troviamo rispetto al piano; possiamo dire, quindi, che se due punti si trovano alla stessa distanza dal piano, ma in parti opposte rispetto ad esso, i vettori campo elettrico in quei punti hanno stesso modulo e stessa direzione, ma versi opposti.

Anche le linee di campo hanno direzione ortogonale al piano, parallele tra loro ed equidistanziate; in questo caso, quindi, la densità delle linee di campo è costante, a conferma del fatto che il modulo del campo elettrico non varia.

Dimostrazione

La dimostrazione della formula che descrive il modulo del campo elettrico può essere effettuata considerando un piano infinito di carica attraversato da una superficie chiusa cilindrica.

La superficie cilindrica è una superficie chiusa, quindi il flusso del campo vettoriale attraverso essa è dato dal teorema di Gauss, e vale:

$Φ_Ω (vec E) = frac(Q_(Tot))(ε)$

Possiamo calcolare il flusso totale anche considerando i singoli flussi sulla superficie laterale del cilindro e sulle due basi. Nel primo caso abbiamo un flusso nullo, in quanto il vettore superficie e il vettore campo elettrico sono perpendicolari; nel secondo caso, invece, il flusso è dato dal prodotto E ∙ ∆S, dove ∆S indica l’area di base del cilindro.

Il flusso totale, quindi, è dato da:

$Φ_Ω (vec E) = E * ∆S + E * ∆S = 2E * ∆S $

Uguagliando le due espressioni del flusso del campo vettoriale, possiamo ricavare E:

$2E * ∆S = frac(Q_(Tot))(ε) to E = frac(Q_(Tot))(2∆Sε) = frac(Q_(Tot))(∆S) * frac(1)(2ε) = frac(σ)(2ε)$

Distribuzione lineare infinita di carica

Una distribuzione lineare infinita di carica è data da un filo infinito su cui si trovano delle cariche elettriche (supponiamo positive) distribuite uniformemente sulla lunghezza.

Consideriamo il vettore campo elettrico in un punto che si trova esternamente alla distribuzione, a distanza r da essa; in questo punto, il vettore ha direzione perpendicolare al filo, e verso dato dal segno della carica (in questo caso verso uscente).

Il modulo del vettore campo elettrico in quel punto è dato dalla formula:

$ E = frac(λ)(2πε_0r)$

dove $ε_0$ è la costante dielettrica del vuoto, mentre λ rappresenta la densità lineare di carica, data dal rapporto tra la carica ∆Q presente in una sezione di filo, e la lunghezza ∆l di tale sezione.

Esercizio

Consideriamo una porzione di un piano infinito uniformemente carico, avente una superficie di $4,0 m^2$; in tale porzione è contenuta una carica di 6,7 μC. Calcolare l’intensità del campo elettrico generato dal piano di carica.

Come sappiamo, il modulo del campo elettrico per una distribuzione piana infinita di carica è dato dal rapporto tra la densità superficiale σ e la quantità 2ε.

Possiamo per prima cosa ricavare il valore di σ dal rapporto tra la carica e la superficie interessata da essa:

$σ = frac(∆Q)(∆S) = frac(4,0 m^2)(6,7 μC) = frac(4,0 m^2)(6,7 * 10^(-6) C) = 0,6 * 10^(-6) m^2/C$

Poi possiamo procedere applicando la formula vista in precedenza, e calcoliamo il rapporto tra la densità superficiale di carica e 2ε, ricordando che il valore di ε è noto:

$ E = frac(σ)(2ε) = frac(1,675 * 10^(-6) m^2/c)(2 * 8,85 * 10^(-12) C^2/(N*m^2)) = 0,0946 * 10^6 N/C = 9,5 * 10^4 N/C$

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

Campi elettrici e distribuzioni sferiche

Prendiamo in considerazione delle distribuzioni di carica con forma particolare, e consideriamo una distribuzione sferica omogenea.

Ipotizziamo, per semplicità, che la distribuzione sferica, di raggio R, si trovi nel vuoto. Esaminiamo tre casi: consideriamo un punto P, e vediamo come cambia il campo elettrico in quel punto se esso si trova all’interno della sfera, sulla superficie sferica, o all’esterno di essa.

P esterno alla sfera

Consideriamo una sfera conduttrice in cui le cariche sono distribuite in modo uniforme sulla superficie. All’interno della sfera il campo elettrico è nullo, quindi calcoliamo il campo elettrico in un punto che si trova esternamente ad essa.

Scegliamo, quindi, il punto P esterno alla sfera, ad una distanza r dal centro O di essa. In ogni punto esterno alla sfera, e quindi anche in P, il vettore campo elettrico ha direzione radiale (il suo verso è dato dal segno della carica sulla superficie sferica); per determinare, quindi, il campo elettrico nel punto P è conveniente scegliere una superficie gaussiana sferica di centro O e raggio r, passante quindi per P.

In ogni punto della superficie gaussiana creata, il vettore superficie ha direzione perpendicolare all superficie, e verso uscente da essa; di conseguenza, il vettore superficie e il vettore campo elettrico nel punto P sono paralleli, cioè l’angolo formato da essi è di 0°.

Per il teorema di Gauss, quindi, il flusso del campo elettrico nella superficie gaussiana chiusa di raggio r è dato da:

$ Φ_(vec S) (vec E) = frac(Q_(Tot))(ε_0)$

Dalla definizione, inoltre, il flusso del campo elettrico in P è pari al prodotto ES:

$ Φ_(vec S) (vec E) = vec E * vec S = E * S * cos 0° = E * S $

Uguagliando le due espressioni possiamo ricavare il valore del campo elettrico nel punto P; ricordiamo che la superficie sferica è pari a $4πr^2$;

$ E * S = frac(Q_(Tot))(ε_0) to E = frac(Q_(Tot))(ε_0 * 4πr^2)$

P interno alla sfera

Consideriamo una carica Q distribuita in modo uniforme all’interno di una sfera di raggio R; il vettore campo elettrico sul punto P, interno alla sfera, posto a distanza r dal centro O, ha direzione radiale, e verso uscente se la carica è positiva, altrimenti verso entrante.

Scegliamo una superficie gaussiana sferica centrata in O e di raggio r, pari alla distanza di P da O (r>R).

Il campo elettrico all’interno della sfera è direttamente proporzionale alla distanza del punto P dal centro della sfera; il modulo del vettore campo elettrico sul punto P è dato dalla seguente formula:

$E = frac(Q_(Tot) * r)(ε_0 * 4πR^3)$

P sulla superficie della sfera

In questo caso non occorre servirsi di un’ulteriore superficie gaussiana, perché possiamo calcolare il campo elettrico semplicemente considerando la superficie sferica che origina la carica.

In questo caso, quindi, con ragionamenti analoghi ai precedenti, possiamo ricavare il modulo del vettore campo elettrico dalla seguente uguaglianza:

$ E * S = frac(Q_(Tot))(ε_0)$

La superficie S che dobbiamo considerare, però, è quella della sfera di raggio R, e vale pertanto $S=4πR^2$.

Il modulo del vettore campo elettrico vale quindi:

$E = frac(Q_(Tot))(ε_0 * 4πR^2)$

Osserviamo che il modulo del vettore campo elettrico è uguale a quello di una carica puntiforme; ciò significa che la carica distribuita in modo omogeneo sulla superficie sferica da lo stesso effetto di una carica puntiforme concentrata tutta nel centro della sfera.

Sfera solida uniformemente carica

Consideriamo ora una sfera solida di raggio R, con densità di carica uniforme ρ; calcoliamo il campo elettrico all’interno e all’esterno della sfera.

All’esterno della sfera si procede scegliendo una superficie gaussiana costituita da una sfera cava di raggio r; procedendo come sopra, si trova il valore del campo elettrico in un punto esterno alla sfera. In questo caso, però, conosciamo anche la densità volumica di carica, e possiamo esprimere la carica Q in funzione della densità.

La formula che si ottiene è la seguente:

$E = frac(ρ * R^3)(3 ε_0 r^2)$

Anche nel caso di un punto interno alla sfera si sceglie una superficie gaussiana costituita da una sfera cava di raggio r, e si calcola il campo elettrico relativo a tale superficie.

Si ricava, poi, il valore del campo elettrico in funzione della densità di carica:

$E = frac(ρ * r)(3 ε_0 )$

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

L’energia potenziale elettrica

Abbiamo visto che la forza di attrazione gravitazionale è una forza conservativa, e in quanto tale gode di alcune proprietà: il lavoro compiuto dalla forza è indipendente dal cammino scelto, ma dipende solo dalle posizioni iniziale e finale; vale la conservazione dell’energia meccanica in seguito all’applicazione della forza; tramite essa può essere descritta la grandezza energia potenziale.

Ricordiamo che l’energia potenziale gravitazionale, pari a U=mgh, dipende dalla scelta arbitraria del livello zero di energia potenziale; tuttavia, la differenza di potenziale è indipendente da tale scelta.

La differenza di energia potenziale è strettamente collegata al lavoro compiuto dalla forza; in particolare, se un corpo passa dalla posizione A alla posizione B, il lavoro compiuto da una forza conservativa in tale passaggio è dato da:

$ W_(A to B) = -∆U$

La forza di Coulomb, abbiamo visto, è per molti aspetti simile alla forza di Newton, se pur con qualche differenza. Tuttavia, la stessa forma matematica delle due forze fa si che esse abbiamo anche le stesse proprietà; in particolare possiamo affermare che entrambe le forze sono conservative.

Possiamo, quindi, definire anche per la forza elettrica un’energia potenziale elettrica.

In questo caso, definiamo l’energia potenziale elettrica come l’opposto del lavoro compiuto dalla forza elettrostatica per portare una carica Q da una posizione iniziale A ad una posizione finale B.

Ricordiamo che nel caso della forza gravitazionale, l’energia potenziale è data dalla seguente formula:

$ U = – G * frac(m_1 * m_2)(r) + k$

dove k è una costante, e dipende dalla scelta che si effettua per il livello zero di energia potenziale.

In analogia con la forza di Newton ,quindi, possiamo ricavare, dall’espressione delle relative forze, una formula anche per l’energia potenziale elettrica; definiamo, quindi U in questo modo:

$ U = frac(1)(4πε_0) * frac(Q_1 * Q_2)(r) + k$

Per convenzione, poi, si sceglie di porre il livello zero di energia potenziale quello in cui le cariche si trovano a distanza infinita; di conseguenza si ottiene un valore di k pari a zero.

Notiamo che, a differenza dell’energia potenziale gravitazionale, l’energia potenziale elettrica è stata definita con segno positivo. Infatti, per convenzione, si scrivono le forze di tipo attrattivo con segno meno, mentre quelle di tipo repulsivo con segno più. Per questo, la formula della forza di Coulomb è stata scritta con segno positivo.

Energia potenziale elettrica nel caso di un sistema formato da più cariche

Nel caso in cui sono presenti nello spazio più cariche puntiformi, l’energia potenziale totale del sistema si ottiene considerando le energie potenziali di tutte le coppie di cariche considerate singolarmente, prese in tutti i modi possibili, e sommandole tra loro.

Consideriamo un sistema formato da tre cariche $Q_1$, $Q_2$ e $Q_3$; chiamiamo $U_(1,2)$ , $U_(1,3)$ e $U_(1,4)$ rispettivamente le energie potenziali che riguardano le coppie di cariche $[Q_1 , Q_2]$, $[Q_1 , Q_3]$ e $[Q_2 , Q_3]$.

Per determinare l’energia potenziale complessiva si procede immaginando di allontanare all’infinito le cariche una alla volta.

Cominciamo, ad esempio, dalla carica $Q_1$; se essa viene allontanata dalle altre fino a raggiungere distanza infinita, il lavoro compiuto dalla forza elettrica dovuta alle cariche $Q_2$ e $Q_3$ in tale spostamento è dato dalla somma dei lavori che sarebbero compiuti dalle cariche $Q_2$ e $Q_3$ se esse si trovassero sole con $Q_1$; il lavoro complessivo vale quindi:

$ W_1 = U_(1,2) + U_(1,3)$

Supponiamo, ora, di allontanare anche una delle altre cariche rimaste, ad esempio $Q_2$; il lavoro che la forza elettrica dovuta alla presenza di $Q_3$ compie quando $Q_2$ è portata a distanza infinita da essa è dato da:

$ W_2 = U_(2,3)$

L’unica carica che rimane ora è $Q_3$, che però già si trova a distanza infinita dalle altre; di conseguenza, il lavoro totale che è stato svolto durante questi passaggi è dato dalla somma di $W_1$ e $W_2$:

$W_(Tot) = W_1 + W_2 = U_(1,2) + U_(1,3) + U_(2,3) $

Il lavoro totale, quindi, corrisponde proprio alla somma delle energie potenziali di tutte le coppie di cariche presenti nel sistema.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

Il potenziale elettrico

Definizione

Nel caso del campo elettrico, abbiamo visto che per studiare gli effetti del campo elettrico generato da una carica puntiforme Q occorreva posizionare una carica di prova q in una zona interessata dal campo elettrico; l’importante era che la carica di prova fosse sufficientemente piccola da non influenzare con la sua carica il campo elettrico generato da Q.

Abbiamo visto che esiste una grandezza vettoriale, il vettore campo elettrico, che dipende esclusivamente dalla carica generatrice, e non dalla carica di prova.

E’ possibile individuare anche una grandezza scalare che sia indipendente dalla carica di prova q, e tale grandezza si definisce a partire dall’energia potenziale.

Ipotizziamo di avere un numero N di cariche, e studiamo gli effetti che tali cariche creano in uno spazio; per farlo, posizioniamo una carica di prova q all’interno di esso.

Per determinare l’energia potenziale relativa alla carica di prova q, nel punto in cui essa si trova, dobbiamo calcolare l’energia potenziale di q con ciascuna delle cariche $Q_1$ , $Q_2$, …, $Q_N$ che compongono il sistema; la somma delle energie potenziali fornirà il valore dell’energia complessiva, che indichiamo con UA.

A partire da queste considerazioni, possiamo definire una nuova grandezza scalare, che prende il nome di potenziale elettrico; il potenziale elettrico in un punto P è definito come il rapporto dell’energia potenziale nel punto P e la carica di prova q:

$ V_P = frac(U_P)(q)$

Il potenziale elettrico è indipendente dalla carica di prova, in quanto l’energia potenziale è direttamente proporzionale ad essa.

Nel Sistema Internazionale, il potenziale elettrico si esprime in J/C, e tale grandezza prende il nome di volt (v).

Possiamo calcolare il potenziale elettrico generato da una carica puntiforme in un punto P che si trova ad una distanza r da essa. Per farlo, occorre considerare una carica di prova posta nel punto P, e calcolare l’energia potenziale della carica in quel punto.

Poiché l’energia potenziale nel punto P si ottiene dalla formula:

$ U = frac(1)(4πε) * frac(Q*q)(r) $

il potenziale elettrico nel punto P si ottiene dividendo tale energia potenziale per la carica di prova:

$ V = frac(U)(q) = frac(1)(4πε) * frac(Q*q)(r) * 1/q = = frac(1)(4πε) * frac(Q)(r)$

Questa formula è un’ulteriore conferma del fatto che il potenziale è indipendente dalla carica di prova, ma dipende esclusivamente dalla carica generatrice.

Nel caso in cui si abbia un campo elettrico generato da più cariche, il potenziale totale in un punto P si ottiene ponendo una carica di prova q in P, e calcolando i singoli potenziali tra q e ciascuna carica che genera il campo. La somma totale di tutti i singoli potenziali fornisce il valore del potenziale totale.

La differenza di potenziale

Come sappiamo, l’energia potenziale elettrica è uguale al lavoro negativo che compie la forza elettrica quando una carica viene portata da un punto A ad un punto B.

Nel punto iniziale A e nel punto finale B possiamo calcolare il potenziale elettrico, dato dal rapporto dell’energia potenziale in quei punti sulla carica di prova; avremmo quindi:

$ V_A = frac(U_A)(q) , V_B = frac(U_B)(q)$

Possiamo definire la differenza di potenziale tra il punto A e il punto B come differenza del potenziale in B meno il potenziale in A:

$ ∆V = V_B – V_A = frac(U_B)(q) – frac(U_A)(q) = frac(∆U)(q)$

Dalla definizione di energia potenziale come lavoro, possiamo riscrivere la differenza di energia potenziale anche come rapporto negativo del lavoro da A a B sulla carica di prova:

$ ∆V = frac(∆U)(q) = – frac(W_(AtoB))(q)$

Possiamo stabilire, in base al segno del lavoro compiuto dalla forza elettrica durante lo spostamento, se questo è avvenuto in maniera spontanea o meno.

Ad esempio, nel caso di cariche positive, se la forza elettrica compie un lavoro W > 0, la differenza di potenziale è negativa; ciò significa che le cariche positive si spostano spontaneamente da punti a potenziale maggiore verso punti a potenziale minore.

Nel caso di cariche negative, invece, vale l’opposto; esse si muovono spontaneamente da punti a potenziale minore verso punti a potenziale maggiore.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

La circuitazione del campo elettrico

La circuitazione è un concetto matematico che riguarda un cammino lungo un percorso chiuso in un campo vettoriale.

Consideriamo, quindi, un percorso chiuso che si trova all’interno di un campo elettrico; quando si percorre una linea chiusa occorre innanzitutto stabilire un verso di percorrenza di esso.

Successivamente, si procede dividendo il percorso, che chiamiamo L, in n parti, in modo che ogni singola parte possa essere considerata un segmento di retta. Lungo ciascuna di queste parti calcoleremo il valore del campo elettrico.

Indichiamo, quindi, con $∆s_i$ il vettore spostamento che individua il tratto i-esimo, e indichiamo con $E_i$ il vettore campo elettrico presente nei punti di tale segmento.

circuitazione-campo-elettrico

Si definisce, quindi, circuitazione del campo elettrico lungo la superficie L la somma dei prodotti scalari, in ciascun tratto, dei vettori spostamento ∆si e dei vettori campo elettrico in quel punto:

$ Γ_L (vec E) = vec E_1 * ∆ vec S_1 + …. + vec E_n * ∆ vec S_n = \sum_{i=1}^n (vec E_i * ∆ vec S_i)$

Dalla definizione di circuitazione, e dal fatto che la forza elettrostatica è una forza conservativa, possiamo dedurre che la circuitazione del campo elettrico lungo un percorso chiuso è uguale a zero; ovvero, che il lavoro compiuto dalla forza elettrica lungo un cammino chiuso è nulla.

Procediamo moltiplicando la formula della circuitazione del campo elettrico per una carica di prova q:

$ q * Γ_L (vec E) = q * \sum_{i=1}^n (vec E_i * ∆ vec S_i) = \sum_{i=1}^n q*(vec E_i * ∆ vec S_i) $

$ = \sum_{i=1}^n (vec F_i * ∆ vec S_i) $

Notiamo che all’interno della sommatoria compare un prodotto scalare della forza per lo spostamento: tale prodotto scalare è proprio quello della definizione di lavoro nel caso di un campo di forze.

La circuitazione lungo un percorso chiuso, quindi, corrisponde proprio al lavoro svolto dalla forza lungo tale percorso, ma solo nel caso in cui ci troviamo in un campo di forze.

Nel caso di un campo elettrico, però, la circuitazione non rappresenta la stessa cosa, in quanto campo elettrico e forza sono dimensionalmente diversi.

Tuttavia, sappiamo che ogni carica elettrica che si trova all’interno di un campo elettrico possiede un’energia potenziale elettrostatica, definita proprio come il lavoro compiuto alla forza elettrica quando la carica situata in quel punto viene spostata da un punto iniziale ad un punto finale.

La circuitazione di un percorso chiuso semplice

Consideriamo un percorso chiuso molto semplice, come quello in figura:

circuitazione-del-campo-elettrico

Calcoliamo il lavoro compiuto dalla forza elettrica nei singoli tratti, relativo agli spostamenti di una carica q da A a B, da B c C e da C ad A: il lavoro in ciascun tratto si ottiene come opposto della differenza di energia potenziale nei singoli tratti:

$ W_(Tot) = W_(AtoB) + W_(BtoC) + W_(CtoA) = (U_A – U_B) + (U_B – U_C) + (U_C – U_A) = 0$

Se dividessimo per q il lavoro svolto percorrendo il cammino chiuso, riotterremmo la circuitazione del campo elettrico lungo tale percorso; essendo, però, il lavoro lungo il percorso chiuso uguale a zero, abbiamo che anche la circuitazione lungo un percorso chiuso è nulla.

Possiamo giungere allo stesso risultato notando che il prodotto scalare del vettore campo elettrico con il vettore spostamento non è altro che l’opposto della differenza di potenziale; questo fatto può essere dedotto dalla formula della differenza di potenziale come rapporto negativo tra il lavoro e la carica di prova:

$ ∆V = – frac(W_(AtoB))(q) = – frac(q * vec E * ∆vec S)(q) = – vec E * ∆ vec S$

Possiamo, quindi, sostituire questa formula all’interno della formula della circuitazione del campo elettrico, e quindi abbiamo:

$ Γ_L (vec E) = \sum_{i=1}^n (vec E_i * ∆ vec S_i) = \sum _{i=0}^n (- ∆V_i)$

Dato che in ogni tratto del percorso chiuso la differenza di potenziale è nulla, sarà nulla anche la differenza di potenziale lungo tutto il percorso.

Infatti, spostandoci lungo un percorso chiuso, dal punto iniziale al punto finale, dopo aver percorso tutta la lunghezza, si ritorna al punto di partenza; di conseguenza, la differenza di potenziale tra il punto iniziale e quello finale è necessariamente uguale a zero.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

Introduzione all’ elettrostatica

Consideriamo alcuni conduttori che si trovano in un particolare stato di equilibrio, detto equilibrio elettrostatico; tale situazione di equilibrio si ha quando le cariche che costituiscono il sistema sono ferme, e il campo elettrico non varia.

Una delle caratteristiche principali di un conduttore in equilibrio elettrostatico è il fatto che la carica elettrica all’interno di esso è nulla; tutte le cariche presenti, infatti, si distribuiscono sulla sua superficie.

La dimostrazione di questo fatto deriva dal teorema di Gauss: consideriamo una superficie chiusa presente all’interno del conduttore:

teorema-di-gauss

sappiamo che il flusso del campo elettrico all’interno di essa è nullo; di conseguenza, possiamo dedurre che anche la carica presente all’interno di esso sia nulla.

$Φ = frac(Q)(ε_0) = 0 to Q = 0$

Esaminiamo ora il campo elettrico e il potenziale elettrico di un conduttore carico in equilibrio elettrostatico.

Come abbiamo visto, la carica presente sul conduttore si concentra sulla sua superficie; all’interno di esso, invece, la carica totale è nulla (cioè le cariche positive sono in numero uguali a quelle negative).

Sappiamo, però, che le cariche negative sono in grado di muoversi all’interno di un corpo conduttore; e le cariche si muovono per effetto del campo elettrico. Dato che il conduttore è in equilibrio elettrostatico, e che quindi tutte le cariche elettriche in esso sono ferme, possiamo concludere che anche il campo elettrico di un conduttore all’equilibrio elettrostatico è nullo.

Sulla sua superficie, invece, il vettore campo elettrico ha direzione perpendicolare alla superficie stessa; il suo verso sarà entrante nella superficie se le cariche in esso sono negative, altrimenti il verso sarà uscente.

Per quanto riguarda il potenziale elettrico, si può dimostrare che in un conduttore carico all’equilibrio elettrostatico il campo potenziale ha lo stesso valore in tutti i punti interni e sulla superficie dell’oggetto.

In particolare, si dice che la superficie esterna di tale conduttore è una superficie equipotenziale.

Un’altra interessante caratteristica dei conduttori è che la carica elettrica non si distribuisce uniformemente all’interno di essi, se essi non hanno una forma regolare.

Se il conduttore presenta delle parti più appuntite di altre, le cariche elettriche tendono a concentrarsi su di esse; le punte, infatti, hanno la caratteristica di attirare o disperdere facilmente la carica elettrica.

Questo spiega perché, in caso di temporale fulmini, è sconsigliato utilizzare ombrelli con punta metallica, o avvicinarsi ad alberi dalla forma appuntita.

La densità superficiale di carica

Se consideriamo conduttori elettrici di forma regolare, come ad esempio una sfera cava, la carica elettrica di distribuisce uniformemente sulla loro superficie.

Per questo, nel casi di questi particolari conduttori, si può parlare di densità superficiale di carica; essa esprime la quantità di carica elettrica presente sulla superficie, ed è data dal rapporto tra la carica che si trova in una precisa area della superficie e l’area della superficie stessa.

$ σ = frac(∆Q)(∆S)$

tale densità risulta sempre la stessa in ogni punto della sfera.

Anche nel caso di conduttori pieni, come una sfera piena, la carica si distribuisce uniformemente all’interno di essa; in questo caso, però, si parla di densità volumica di carica, data dal rapporto tra la carica presente in una determinata sezione e il volume di tale sezione:

$ σ = frac(∆Q)(∆V)$

Anche la densità volumica di carica è la stessa in ogni punto del corpo, purché il corpo sia di forma regolare; come abbiamo detto in precedenza, se il corpo presenta delle punte, o delle parti con curvature più accettate, la carica elettrica si dispone maggiormente in quelle zone; di conseguenza, esse presenteranno densità di carica maggiore.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: La legge di Coulomb

Appunti: Il campo elettrico

Appunti: Le linee di campo

Il teorema di Coulomb

Quando si studia un fenomeno di elettrostatica, l’analisi di tale fenomeno riguarda l’individuazione delle caratteristiche principali dei conduttori che generano un campo elettrico: il potenziale elettrico, o il campo elettrico in ogni punto dello spazio.

Determinare queste caratteristiche significa risolvere il cosiddetto problema generale dell’elettrostatica, purché si conosca la disposizione dei conduttori nello spazio, e di sapere la cariche che si trova su ciascuno di essi.

La scelta del livello zero di energia potenziale

Per prima cosa, se si decide di studiare il potenziale elettrico in tutti i punti dello spazio, occorre inizialmente stabilire dove porre il livello zero del potenziale.

Sappiamo che tale scelta è arbitraria, ma solamente si considerano le tre scelte più comuni: all’infinito, a terra, o al potenziale di massa. Ciascuna scelta risulterà più adatta in base al contesto in cui si vuole studiare un determinato conduttore.

Spesso si sceglie di porre il livello zero di energia potenziale nel punto in cui la distanza tra la carica che genera il campo elettrico e tale punto risulta infinita; questa scelta può essere vantaggiosa nel caso in cui il campo elettrico è generato da una quantità finita di cariche puntiformi.
La scelta di porre il livello zero di energia potenziale come quello in cui si trova la Terra è spesso impiegato nelle industrie, o nel campo di altri tipi di produzioni; in questo ambito, quando un conduttore viene collegato alla Terra per mezzo di un tubo conduttore, esso raggiunge lo stesso potenziale posseduto dalla Terra, e si dice pertanto “messo a terra”.
La terza scelta, quella che riguarda il potenziale di massa, viene spesso utilizzata nel caso in cui il conduttore in questione sia isolato dal Terreno, e non possa essere nesso a terra, come ad esempio nel caso delle automobili (le ruote, infatti, fungono da isolante); in questo caso, il livello zero di energia potenziale è quello in cui si trova l’involucro metallico che costituisce il conduttore. Se un conduttore è collegato a tale involucro, e quindi raggiunge lo stesso potenziale, si dice che esso è “messo a massa”.

In generale, non sempre è possibile dare una soluzione definitiva al problema generale dell’elettrostatica, e molto spesso sono necessarie tecniche e conoscenze di livello superiore.

Il teorema di Coulomb

Tuttavia, se si conosce il valore del vettore campo elettrico in ogni punto dello spazio, è possibile applicare il teorema di Coulomb per ottenere informazioni aggiuntive sul campo elettrico che stiamo studiando.

Il teorema afferma che, in casi di equilibrio elettrostatico, in un punto che si trova sulla superficie di un conduttore, il modulo del vettore campo elettrico è dato dal rapporto tra la densità superficiale di carica in quel punto e la costante dielettrica assoluta del mezzo in cui si trova il conduttore:

$ E = frac(σ)(ε)$

Come abbiamo già visto precedentemente, se il conduttore non ha una forma regolare, ma presenta delle sporgenze o delle punte, la densità di carica non è uniforme in esso, e le zone più acuite sono quelle che presentano densità di carica maggiore.

Il campo elettrico e le punte

Dal teorema di Coulomb si può notare che il campo elettrico è direttamente proporzionale alla densità di carica; ciò significa che se un conduttore presenta delle sporgenze o delle punte, in prossimità di esse il campo elettrico è particolarmente intenso.

Una conseguenza di questo fatto, è il cosiddetto potere delle punte, che può essere facilmente notato anche per via sperimentale.

Il potere delle punte è un fenomeno dovuto alla presenza, nell’aria, di particelle cariche, o di molecole ionizzate; a causa della presenza del forte campo elettrico sulle punte del conduttore, le particelle tendono ad essere attratte verso la punta, o respinte da essa, in base al loro segno.

Ad esempio, se il conduttore è fisso, la punta può generare una corrente d’aria, se le molecole ionizzate vengono respinte da essa.

correnti-e-punte — La punta del conduttore carico genera una corrente d’aria che sposta la fiammella della candela.

Se invece, il conduttore si trova su un supporto in grado di ruotare, e le particelle vengono respinte dalle punte, l’effetto sarà una rotazione nel senso opposto a quello in cui sono rivolte le punte.

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: Introduzione all’elettrostatica

Appunti: Il campo elettrico

Appunti: Le linee di campo

Appunti: Condensatori in seire e in parallelo

Appunti: L’effetto Joule

Appunti: Processo di carica e scarica di un condensatore

Il condensatore piano

Un condensatore piano è un dispositivo costituito da due piastre metalliche parallele, che prendono il nome di armature; esse sono poste ad una certa distanza l’una dall’altra.

Per far funzionare l’apparecchio, le lastre vengono caricate con cariche di segno opposto.

Vediamo ora come di procede per caricare un condensatore piano.

Ipotizziamo che, inizialmente, entrambe le armature siano messe a terra, e posseggano quindi lo stesso potenziale della terra.

Se poi una di esse viene caricata con una carica Q positiva, e l’altra rimane a terra, automaticamente sulla faccia interna di quest’ultima si induce una carica pari a -Q (l’elettrizzazione della seconda lastra avviene per induzione).

La capacità

Quando conferiamo la carica Q alla prima lastra, essa passa da un potenziale elettrico pari a zero al potenziale V; per via sperimentale si nota che la carica che si trova sul conduttore è direttamente proporzionale al potenziale che essa assume.

E’ utile, quindi, introdurre una nuova grandezza, valida per qualsiasi conduttore isolato che passa da uno stato iniziale a potenziale nullo ad uno stato finale a potenziale V.

Questa nuova grandezza si definisce capacità elettrostatica del conduttore, e si indica come rapporto tra la carica Q e il potenziale elettrico:

$C = Q/V$

La capacità di un conduttore si indica, nel Sistema Internazionale, in farad (F), dal nome del fisico Michael Faraday che si cimentò in questi studi.

Anche nel caso di un condensatore piano, essendo esso un conduttore, possiamo parlare ci capacità; in questo caso, si definisce capacità del condensatore come il rapporto tra la carica assunta dalla prima lastra e la divergenza di potenziale tra le due armature:

$C = frac(Q)(∆V)$

Come nel caso di un conduttore generico, anche la capacità del condensatore dipende dalla sua forma e dalle sue dimensioni.

Il campo elettrico

Il condensatore piano può essere rappresentato, in maniera ideale, considerando due distribuzioni piane infinite di carica, parallele, e poste ad una certa distanza l’una dall’altra.

Come abbiamo visto nel caso della distribuzione piana infinita di carica, è possibile trovare una formula che esprima il campo elettrico generato da tale distribuzione. Il campo elettrico, in quel caso, era dato dal rapporto:

$E = frac(σ)(2ε)$

In un condensatore si ha una situazione leggermente diversa; in ogni punto dello spazio, interno o esterno alle due lastre, il campo elettrico totale è dato dalla somma (vettoriale) del campo elettrico generato da ciascuna delle due piastre.

Ricordiamo che il vettore campo elettrico è entrante per la lastra con carica negativa, e uscente per la piastra con carica positiva.

E’ possibile, quindi, dedurre che all’esterno delle due lastre il contributo al campo elettrico di ciascuna di esse fa si che il campo elettrico totale sia nullo; all’interno di esse, invece, il campo elettrico è doppio rispetto a quello generato da ogni singola armatura.

Inoltre, all’interno delle armature, il campo elettrico è uniforme, e il vettore ha direzione ortogonale alle lastre, e verso diretto da quella positiva a quella negativa.

Il campo elettrico all’esterno e all’interno di un condensatore piano a lastre parallele uniformemente carico.

L’intensità del campo elettrico, quindi, si deduce dalla formula di quello di una distribuzione piana infinita di carica, moltiplicando questo per due:

$E = frac(σ)(ε)$

Capacità del condensatore conoscendo il campo elettrico

Conoscendo l’espressione dell’intensità del campo elettrico, possiamo dedurre la capacità del condensatore in un’altra espressione.

Ricordiamo che è possibile esprimere il modulo cel campo elettrico come rapporto tra la differenza di potenziale e ∆s, che in questo caso equivale alla distanza tra le due armature, e che indichiamo con d; svolgiamo, quindi, i passaggi:

$ E = frac(∆V)(∆S) = frac(∆V)(d) to ∆V = E * d = frac(σ)(ε) * d$

La densità superficiale di carica, inoltre, può essere espressa come rapporto tra la carica e la superficie, cioè l’area di un’armatura:

$ σ = Q/S to ∆V = frac(σ)(ε) * d = frac(Q)(S) * frac(d)(ε) $

Poiché la capacità del condensatore è data dal rapporto tra la carica Q e la differenza di potenziale, abbiamo la formula cercata:

$C = frac(Q)(∆V) = frac(Q)(frac(Q)(S) * frac(d)(ε)) = frac(S * ε)(d)$

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: Il campo elettrico

Appunti: Le linee di campo

Appunti: Condensatori in seire e in parallelo

Appunti: L’effetto Joule

Appunti: Processo di carica e scarica di un condensatore

Condensatori in serie e in parallelo

I condensatori sono spesso utilizzati all’interno di dispositivi e circuiti elettrici con lo scopo di accumulare carica nel circuito.

Se ci sono più condensatori, quindi, essi devono essere collegati tra loro per permettere alla corrente elettrica di circolare, e il modo in cui tali condensatori sono collegati fa si che essi vengano divisi in due categorie: i condensatori in serie e i condensatori parallelo.

Quando si studia un sistema formato da più condensatori messi insieme l’effetto complessivo del sistema da essi formato viene descritto dalla capacità equivalente della rete. Possiamo definire la capacità equivalente come la capacità di un singolo condensatore che, essendo sottoposto alla stessa differenza dei potenziale della rete totale, assorbe la stessa carica elettrica.

Come sappiamo, la capacità di un conduttore è data dal rapporto tra la carica assorbita e il potenziale elettrostatico; possiamo, quindi, scrivere la capacità equivalente come rapporto della carica elettrica relativa all’intera rete sul potenziale cui essa è soggetta:

$ C_(eq) = frac(Q_(eq))(V)$

Definito il concetto di capacità equivalente, vediamo ora le principali caratteristiche dei condensatori in serie e in parallelo.

Consideriamo nel nostro discorso solo dei condensatori ideali, cioè dei condensatori che una volta caricati, non necessitano di forze ulteriori per essere mantenuti carichi.

Nella realtà, invece, questo non accade, e un condensatore carico deve essere collegato ad un apparecchio che permetta alla differenza di potenziale fra le armature di rimanere costante. All’interno di un circuito reale, quindi, sono presenti anche dei generatori o delle pile.

I condensatori in parallelo

I condensatori in parallelo sono condensatori che vengono collegati tra loro in modo che, ai loro estremi, sia presente la stessa differenza di potenziale.

Solitamente, i condensatori collegati in parallelo vengono rappresentati come in figura:

condensatori-in-prallelo — Condensatori in parallelo

Più condensatori in parallelo, inoltre, sono equivalenti ad uno stesso condensatore che possiede una capacità, pari alla capacità equivalente dell’intero circuito, data dalla somma delle capacità di ciascun singolo condensatore.

Vediamo come è stato possibile giungere a questa affermazione partendo dal caso più semplice, quello in cui si hanno solo due condensatori collegati in parallelo.

Ipotizziamo di conoscere la carica presente su ciascun condensatore e la differenza di potenziale del circuito, che equivale anche alla differenza di potenziale presente tra le armature di ciascun condensatore.

La carica elettrica totale è data dalla somma delle cariche elettriche presenti su ciascun condensatore; di conseguenza, possiamo ricavare il loro valore partendo dai dati noti, e ricordando la definizione di capacità:

$ C_1 = frac(Q_1)(V) , C_2 = frac(Q_2)(V) to Q_1 = C_1 * V , Q_2 = C_2 * V $

Determiniamo, quindi, l’espressione della carica totale:

$ Q_(eq) = Q_1 + Q_2 = C_1 * V + C_2 * V = (C_1 +C_2) * V $

Da questa espressione possiamo ricavare il valore della capacità equivalente del circuito che, come volevamo dimostrare, è uguale alla somma delle capacità dei singoli condensatori:

$C_(eq) = frac(Q_(eq))(V) = C_1 + C_2$

Questo ragionamento può essere esteso al caso generale di un circuito costituito da un numero n di condensatori; in questo caso, possiamo esprimere la capacità equivalente come:

$C_(eq) = C_1 + C_2 + ….. + C_n = \sum_{i=1}^n C_i $

Condensatori in serie

In un collegamento in serie, quando si conferisce una carica al sistema per induzione, ogni condensatore presente sul circuito si carica di quella stessa carica, cosicché tutti i condensatori abbiano la stessa carica elettrica Q.

Un collegamento in serie si rappresenta come quello in figura:

condensatori-in-serie — Condensatori in serie

A differenza dei collegamenti in parallelo, in questo caso la differenza di potenziale del circuito è differente da quella di ciascuna carica, ed è data dalla somma di ciascuna di esse; nel caso di un circuito formato da n condensatori si ha:

$ ∆V = ∆V_1 + ∆V_2 + …. + ∆V_n = \sum_{i=1}^n ∆V_i $

A ciascuna differenza di potenziale ∆Vi corrisponde un condensatore di capacità Ci, pari al rapporto tra la carica Q e la differenza di potenziale corrispondente.

$C_i = frac(Q)(∆V_i)$

La differenza di potenziale totale, quindi, è data dalla somma dei rapporti tra la carica Q e le singole capacità;

consideriamo, come prima, il caso semplice di un circuito costituito da due soli condensatori in serie; abbiamo quindi:

$ ∆V = ∆V_1 + ∆V_2 = frac(Q)(C_1) + frac(Q)(C_2) = (frac(1)(C_1) + frac(1)(C_2))Q $

Possiamo ricavare, quindi, la capacità equivalente, e da questa anche il suo reciproco:

$ C_(eq) = frac(Q)(∆V) to frac(1)(C_(eq)) = frac(∆V)(Q) = frac(1)(C_1) + frac(1)(C_2) $

Si può, quindi, estendere il ragionamento al caso di un circuito formato da n condensatori collegati in serie; si ottiene che il reciproco della capacità equivalente è dato da:

$frac(1)(C_(eq)) = frac(1)(C_1) + frac(1)(C_2) + … + frac(1)(C_n) = \sum_{i=1}^n frac(1)(C_i) $

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: L’effetto Joule

Appunti: Processo di carica e scarica di un condensatore

Energia immagazzinata in un condensatore

Come sappiamo, il condensatore piano è costituito da due lastre metalliche, inizialmente scariche in quanto collegate a terra, che poi vengono caricate di carica Q: in particolare si elettrizza la prima armatura direttamente (ad esempio per mezzo di una pila), mentre l’altra assumerà una carica opposta -Q per induzione.

Le armature continueranno a caricarsi distribuendo la carica Q uniformemente su tutta la loro superficie fino a quando la differenza di potenziale ∆V tra le armature non avrà raggiunto la differenza di potenziale della pila.

In generale, il processo di carica di un condensatore è un processo che richiede lavoro per essere svolto; infatti, anche se un corpo è inizialmente scarico, su di esso sono comunque presenti delle cariche elettriche, quelle positive in ugual quantità di quelle negative, in modo che il corpo risulti neutro. Quando il corpo viene caricato, quindi, le nuove cariche elettriche che si aggiungono vengono respinte dalle cariche dello stesso segno che erano già presenti sull’armatura, cosicché il processo di elettrizzazione va contro natura, ed è necessaria, quindi, la presenza di una forza esterna (che compie lavoro) che spinga le nuove cariche sulla superficie del conduttore.

In generale, il lavoro è espresso come prodotto della carica per la differenza di potenziale: W = Q ∙ ∆V; possiamo immaginare questo lavoro come la somma di tutti i lavori che occorre compiere per spostare tutte le cariche infinitesime dall’armatura negativa a quella positiva.

E’ necessario questo ragionamento in quanto le grandezze che compaiono nella formula cambiano costantemente durante il processo di elettrizzazione del conduttore, e ciò rende impossibile determinare un valore complessivo del lavoro svolto.

E’ possibile, però, suddividere il processo generale in tanti piccoli intervalli, cosicché in ciascuno di essi sia la carica che la differenza di potenziale risultino costanti; in questo modo è possibile calcolare il lavoro svolto in ognuno dei singoli intervalli, e da questi ottenere il lavoro complessivo, dato dalla somma di tutti i lavori.

Se rappresentiamo in un piano carica-volume questo tipo di processo, il lavoro svolto è calcolabile come l’area sottesa dalla curva che rappresenta il lavoro, ovvero l’integrale della funzione lavoro.

Si può dimostrare che il lavoro complessivamente svolto durante il processo è dato dalla seguente formula:

$ W_c = 1/2 QV$

Ricordando, poi, la relazione tra capacità, carica e potenziale (C=Q/V), possiamo ricavare altre utili formule che esprimono il lavoro:

$ W_c = 1/2 (CV)V = 1/2 CV^2 $ , $ W_c = 1/2 QV(Q/C) = 1/2 frac(Q^2)(C)$

Anche in questo caso vale la conservazione dell’energia; di conseguenza, il lavoro svolto per elettrizzare un condensatore si trasforma poi in energia potenziale, che rimane immagazzinate in esso, e può essere riutilizzata per compiere nuovamente lavoro.

La densità di energia

Come per la carica elettrica, anche per l’energia elettrica, cioè l’energia che viene immagazzinata dal condensatore in seguito al lavoro compiuto per caricarlo, è possibile introdurre il concetto di densità.

Nel caso della carica, la densità veniva indicata come rapporto tra la carica elettrica e la superficie su cui essa si trovava (nel caso di densità superficiale) o il volume su cui si distribuiva (nel caso di densità volumica).

Per l’energia elettrica si definisce densità volumica di energia il rapporto tra l’energia immagazzinata nel condensatore e il suo volume interno:

$ w_(vecE) = frac(W_C)(S*d)$

dove S indica l’area delle armature, mentre d la distanza che le separa.

Questa densità può anche essere espressa in funzione della costante dielettrica del mezzo e del campo elettrico che si trova all’interno del condensatore.

Utilizziamo le formule viste in precedenza all’interno della formula per la densità di energia, e otteniamo la seguente espressione:

$ w_(vecE) =1/2 frac(Q^2)(C) * frac(1)(S*d)$

Ricordiamo che possiamo esprimere la capacità del condensatore come εS/d, e sostituiamo nella formula:

$ w_(vecE) =1/2 frac(Q^2)(C) * frac(1)(S*d) = 1/2 Q^2 * frac(d)(ε*S) * frac(1)(S*d) = 1/2 Q^2 * frac(1)(ε * S^2)$

nella formula possiamo isolare il quadrato del rapporto Q/S, che rappresenta la densità superficiale di carica;

$ w_(vecE) = 1/2 Q^2 * frac(1)(ε * S^2) = 1/(2ε) * (Q/S)^2 = frac(σ^2)(2ε)$

Ora, se vogliamo far comparire all’interno della formula il modulo del campo elettrico, possiamo moltiplicare numeratore e denominatore per ε; il rapporto σ/ε rappresenta proprio E:

$ w_(vecE) = frac(σ^2)(2ε) = ε * frac(σ^2)(2ε^2) = ε/2 * (σ/ε)^2 = ε/2 * E^2$

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: Condensatori in serie e in parallelo

Appunti: L’effetto Joule

Appunti: Processo di carica e scarica di un condensatore

La corrente elettrica e i circuiti

Nei dispositivi elettronici di qualsiasi genere, la corrente circola per permettere il corretto funzionamento grazie a dei circuiti elettrici, cioè degli insiemi di conduttori collegati tra loro e ad un generatore di corrente.

Per corrente elettrica si intende un moto ordinato di cariche elettriche; sappiamo che all’interno di un conduttore le cariche negative, cioè gli elettroni, sono liberi di muoversi; tuttavia vi sono anche dei casi in cui il movimento delle particelle coinvolge anche quelle positive, i protoni.

Il moto di queste particelle è dovuto alla differenza di potenziale che si crea all’interno di un circuito.

Come abbiamo già visto, infatti, le cariche positive tendono a muoversi verso punti a potenziale più basso; quelle negative, invece, si muovono naturalmente da punti a potenziale minore verso punti a potenziale maggiore.

E’ importante sottolineare che viene assegnato un verso di percorrenza del conduttore, che per convenzione si pone come quello che percorrono le cariche positive; il verso di percorrenza, quindi, è quello da punti a potenziale più alto verso punti a potenziale più basso.

La corrente che fluisce all’interno di un circuito è descritta da alcune caratteristiche, una di queste è l’intensità, un parametro che permette di quantizzare la grandezza della carica che attraversa una sezione di un conduttore in un certo intervallo di tempo.

L’intensità di corrente, quindi, di esprime come rapporto tra la carica elettrica e l’intervallo di tempo:

$ i = frac(∆Q)(∆t)$

L’intensità di corrente viene misurata in C/s, che nel Sistema Internazionale si indica come ampere (A).

L’intensità di corrente, poi, può essere costante o variabile nel tempo; in base a questo si possono individuare due tipi differenti di corrente elettrica: la corrente elettrica continua è quella per cui l’intensità di corrente rimane costante nel tempo; altrimenti si parla di corrente alternata.

Possiamo ora introdurre il concetto di circuito elettrico.

Un circuito elettrico è formato da diversi contribuenti: un generatore (ad esempio una pila), dei fili metallici che fungono da conduttori, e un dispositivo che permetta di verificare il passaggio della corrente (ad esempio una lampadina).

Il generatore

Il generatore è necessario per mantenere flusso della corrente; infatti, se non fosse presente un generatore di corrente, le cariche elettriche tenderebbero a muoversi spontaneamente per effetto di una iniziale differenza di potenziale.

Mano a mano che le cariche fluiscono, però, la differenza di potenziale tende a diminuire sempre di più fino ad annullarsi; a questo punto si fermerebbero anche le cariche elettriche, ponendo fine al flusso di corrente.

Un generatore, quindi, permette di ristabilire costantemente la differenza di potenziale, così da mantenere un flusso di corrente continuo.

Per farlo, il generatore trasporta le cariche positive da dove il potenziale è più basso per portarle dove è più alto, così da permettere loro il moto naturale verso punti a potenziale minore; questo processo, per un generatore ideale di tensione continua, avviene sempre e costantemente.

Il circuito elettrico

I circuiti elettrici possono essere aperti o chiusi in base al fatto se vi è passaggio di corrente o meno all’interno di essi; inoltre, come abbiamo visto per i condensatori, anche per i circuiti elettrici si parla di collegamenti in serie e in parallelo.

I circuiti collegati in serie sono quelli che vengono attraversati dalla stessa corrente elettrica; essi sono tali che i conduttori si trovano disposti in successione tra loro.

Generalmente, un circuito di questo tipo viene rappresentato come in figura:

circuiti-elettrici — Circuito elettrico con collegamenti in serie.

Un circuito in cui i conduttori sono collegati in parallelo, invece, è caratterizzato dal fatto che i conduttori hanno tutti le estremità connesse tra loro; di conseguenza essi sono sottoposti alla stessa differenza di potenziale.

Un circuito in parallelo si rappresenta in questo modo:

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: Condensatori in serie e in parallelo

Appunti: Energia immagazzinata in un condensatore

Appunti: L’effetto Joule

Appunti: Processo di carica e scarica di un condensatore

La prima legge di Ohm e i resistori

La prima legge di Ohm

La prima legge di Ohm riguarda una particolare categoria di conduttori, che proprio per questo vengono definiti conduttori ohmici.

Per classificare un conduttore, e poterlo definire ohmico, è necessario costruire e rappresentare la sua curva caratteristica.

Questa curva si rappresenta in un grafico in cui come ascissa si ha la differenza di potenziale, e come ordinata l’intensità di corrente; la curva caratteristica si può determinare per via sperimentale. In questo caso, si procede misurando le variazioni dell’intensità di corrente in un conduttore, al variare della differenza di potenziale ai suoi capi.

Per farlo si considera un circuito in cui un amperometro è collegato in serie con un conduttore, mentre un voltmetro è collegato in parallelo con esso; in questo modo, l’amperometro è attraversato dalla stessa corrente che attraversa il conduttore, e ne può misurare l’intensità di corrente, mentre il voltmetro misura la differenza di potenziale, la stessa del conduttore.

Riportando i dati in un sistema ∆V-i è possibile costruire la curva caratteristica del conduttore; i conduttori che presentano come curve caratteristiche delle rette passanti per l’origine vengono definiti conduttori ohmici.

prima-legge-di-Ohm

Per questo tipo di conduttori l’intensità di corrente è direttamente proporzionale alla differenza di potenziale che viene applicata ai loro capi; questa affermazione rappresenta la prima legge di Ohm, ed è tradotta in simboli dalla seguente formula:

$ i = frac(∆V)(R)$

dove R indica una nuova grandezza fisica, la resistenza elettrica, misurata nel sistema internazionale in V/A, ossia ohm (Ω).

I resistori

Tutti componenti elettrici che soddisfano la prima legge di Ohm vengono definiti resistori.

I resistori, quindi, sono conduttori ohmici, e possono essere ad esempio fili di rame o alluminio, e come tali possono essere collegati tra loro in serie o in parallelo.

In un circuito costituito da più resistori collegati tra loro, ogni resistore possiede una propria resistenza, data dal rapporto tra la differenza di potenziale ai suoi capi e l’intensità di corrente che in esso circola.

E’ importante, però, considerare la resistenza totale del circuito, ossia la resistenza equivalente, definita come quella di un singolo resistore che assorbe dal generatore la stessa corrente elettrica quando è sottoposto alla differenza di potenziale dell’intero circuito.

Vediamo, quindi, come nel caso dei condensatori, che è possibile determinare formulazioni diverse per la resistenza equivalente in base al tipo di collegamenti che sussiste fra i conduttori.

Resistori in serie

I conduttori in serie, come sappiamo, hanno in comune tra loro la stessa intensità di corrente. La differenza di potenziale del sistema, invece, è data dalla somma delle singole differenze di potenziale dei resistori.

Possiamo ricavare da queste considerazioni l’espressione della resistenza equivalente del sistema, applicando la prima legge di Ohm. Consideriamo, per il momento, un circuito formato da due soli resistori:

$ ∆V = ∆V_1 + ∆V_2 = R_1 i + R_2 i = (R_1 + R_2) i $

La resistenza equivalente, quindi, è data dalla somma delle resistenze di ciascun resistore:

$R_(eq) = frac(∆V)(i) = R_1 + R_2 $

Questo ragionamento ha validità generale, e possiamo estenderlo al caso di circuiti formati da n resistori:

$R_(eq) = frac(∆V)(i) = R_1 + R_2 + …. + R_n = \sum_{i=1}^n R_i $

Resistori in parallelo

Per i resistori in parallelo, invece, la corrente elettrica non è la stessa per ogni resistore, ma in ogni diramazione anche la corrente elettrica si divide, e l’intensità è diversa per ciascuno di essi; la somma di tutte le intensità di corrente fornisce l’intensità equivalente del circuito.

La differenza di potenziale ai capi dei resistori, invece, è la stessa del generatore.

Consideriamo un semplice circuito formato solo da sue resistori. Applichiamo la prima legge di Ohm, e determiniamo l’intensità di corrente equivalente:

$ i_(eq) = i_1 + i_2 = frac(∆V)(R_1) + frac(∆V)(R_2) = (frac(1)(R_1) + frac(1)(R_2)) ∆V$

Da questa scrittura, possiamo ricavare il valore del reciproco della resistenza equivalente, dato dalla somma dei reciproci delle resistenze dei singoli resistori:

$ R_(eq) = frac(∆V)(i_(eq)) to frac(1)(R_(eq)) = frac(i_(eq))(∆V) = frac(1)(R_1) + frac(1)(R_2) $

Anche in questo caso possiamo estendere in ragionamento al caso di circuiti formati da n resistori collegati in parallelo:

$ frac(1)(R_(eq)) = frac(1)(R_1) + frac(1)(R_2) + …. + frac(1)(R_n) = \sum_{i=0}^n frac(1)(R_i) $

Potrebbero interessarti

Video Lezioni: Elettromagnetismo

Vide Lezioni: Onde e Luce

Appunti: Condensatori in serie e in parallelo

Appunti: Energia immagazzinata in un condensatore

Appunti: L’effetto Joule