Le forze di contatto: introduzione
Esaminiamo alcuni tipi di forze fondamentali, con le quali abbiamo a che fare ogni giorno, anche se magari non ce ne accorgiamo.
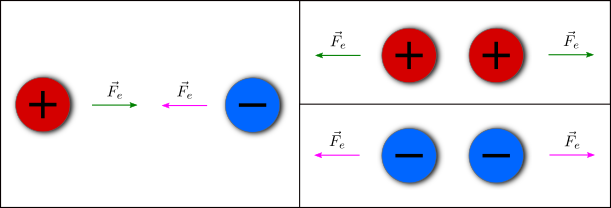
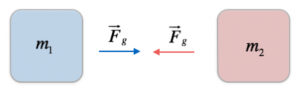
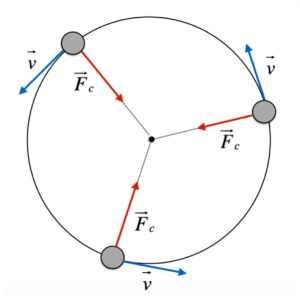
Per cominciare, distinguiamo due tipologie di forze, quelle di contatto e quelle a distanza. Le prime sono forze che possiamo riconoscere facilmente, in quanto avvengono se vi è un contatto tra il corpo che esercita l’azione e quello che la subisce; ad esempio, nel caso di un pallone che viene fatto rotolare. Delle seconde, invece, possiamo solo notare gli effetti, in quanto si hanno senza che vi sia un contatto tra due corpi; ad esempio nel caso di una calamita che attrae un oggetto metallico.
Esaminiamo alcuni tipi di forze di contatto.
La forza di attrito
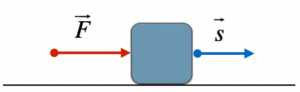
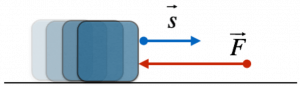
La forza di attrito è una forza di contatto che si oppone al movimento di un corpo; se rappresentata come vettore, la forza di attrito ha direzione contraria a quella del movimento del corpo.
Questo tipo di forza rappresenta un fenomeno microscopico; infatti, l’attrito è dovuto al fatto che, anche se all’apparenza due superfici sembrano perfettamente lisce, in realtà esse presentano delle irregolarità, che incastrandosi tra loro ostacolano il movimento di una superficie sull’altra.

Distinguiamo tre tipi di forze di attrito:
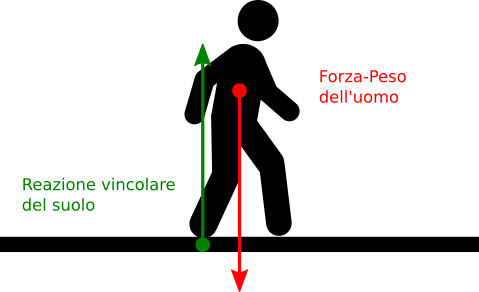
- la forza di attrito radente: è la forza che si esercita tra due superfici che vengono in contatto; questa forza, per esempio, ci permette di camminare, in quanto si esercita tra la suola delle nostre scarpe e il terreno; ci permette quindi di spostarci in avanti.
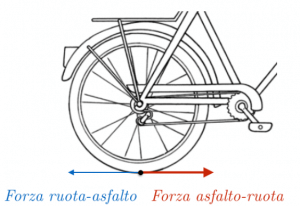
- la forza di attrito volvente: è la forza che si esercita quando un corpo rotola su una superficie, per esempio nel caso delle ruote di un’automobile;
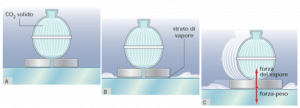
- la forza di attrito viscoso: è la forza che si esercita quando un corpo si muove in un fluido, come nel caso di un aereo che subisce l’impatto dell’aria.
La forza di attrito radente, in particolare, può essere statica, quando le irregolarità microscopiche tra due superfici ferme ostacolano il loro movimento, o dinamica, quando invece le irregolarità oppongono resistenza al moto di due superfici che già si muovono.
L’attrito radente statico
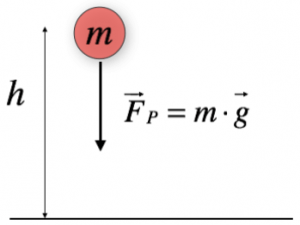
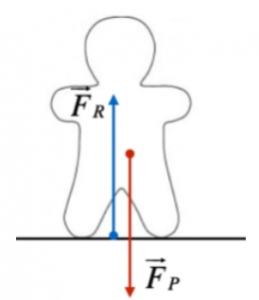
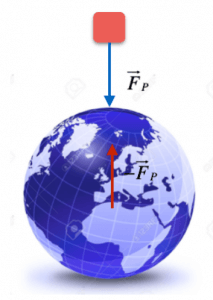
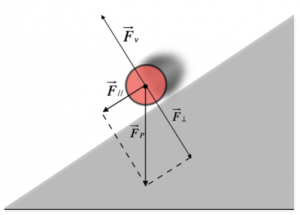
La forza di attrito statico può essere presente anche se nessuno dei due corpi che sono a contatto si muove. Per esempio, se tentiamo di spostare un armadio molto pesante, esercitando una forza su di esso, questo continuerà a rimanere fermo. Questo accade sull’armadio agisce un’alta forza, la forza peso, che lo attrae al suolo, e la nostra forza non è sufficiente a vincerla.
Se, però, tre uomini provassero a spostare tale armadio, probabilmente questo si muoverebbe. Aumentando la forza esercitata, quindi, possiamo vincere la forza peso dell’armadio.
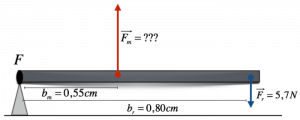
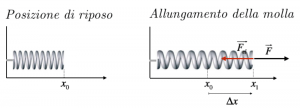
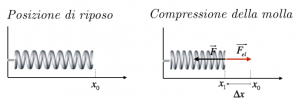
Chiamiamo, quindi, forza al distacco la forza minima che occorre per mettere in moto un oggetto fermo; tale forza è direttamente proporzionale alla forza premente (forza peso), e il suo modulo è dato dalla formula:
$ F_s = μ_s * F_⊥ $
Dove $μ_s$ indica un numero puro, il coefficiente di attrito statico.
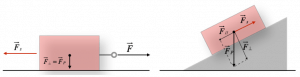
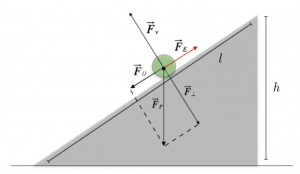
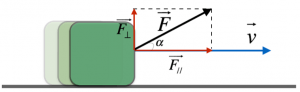
Notiamo che la forza di attrito statico non dipende dall’area di contatto delle superfici; essa è parallela alla superficie di contatto e il suo verso si oppone al movimento.
L’attrito radente dinamico
L’attrito radente dinamico è responsabile del fatto che una sfera in movimento su un piano è destinata, prima o poi, a fermarsi.
Questa forza, quindi, ha verso che si oppone al verso del movimento del corpo, direzione parallela al piano, e modulo direttamente proporzionale a quello della forza premente, e dato dalla formula:
$ F_s = μ_d * F_⊥ $
Dove $μ_d$ indica, anche in questo caso, un numero puro, il coefficiente di attrito dinamico.

Potrebbero Interessarti
Video Lezioni: La dinamica
Video Lezioni: L’energia
Video Lezioni: La dinamica dei sistemi
Video Lezioni: Gli urti
Appunti: Cifre significative e notazione scientifica
Appunti: Le Forze
Appunti: Le forze a distanza: Forze fondamentali
Appunti: Corpi in equilibrio
Appunti: Il momento di una forza
Appunti: Il momento di una coppia di forze
Appunti: Forze che agiscono su un corpo rigido
Appunti: L’equilibrio di un corpo rigido
Appunti: Macchine semplici e leve
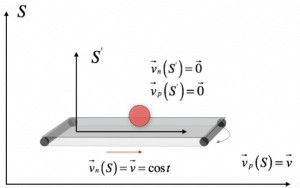
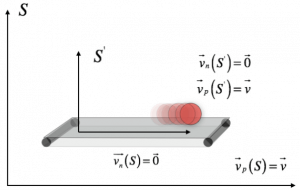
Appunti: Sistemi di riferimento inerziali e il principio di relatività galileiana
Appunti: Il primo principio della dinamica
Appunti: Effetto delle forze sui corpi rigidi, e secondo principio della dinamica
Appunti: Il terzo principio della dinamica