In molti dispositivi elettrici di uso quotidiano l’energia elettrica viene trasformata in calore. Questo processo prende il nome di effetto Joule.
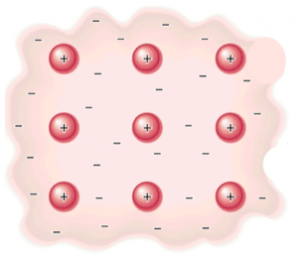
Quando un apparecchio di questo tipo viene messo in funzione, la corrente comincia a fluire nei circuiti interni, e il moto delle particelle che formano la corrente elettrica, favorisce un aumento dell’energia cinetica delle molecole del filo, che di conseguenza si riscalda.
L’energia elettrica, quindi, si trasforma a poco a poco in energia interna del filo.
Il calore che viene prodotto, quindi, è dovuto alla differenza di temperatura tra il filo e l’ambiente circostante; questo permette di convogliare calore in una specifica zona dell’apparecchio, in base al suo funzionamento.
Vediamo ora una spiegazione alternativa dell’effetto Joule, introducendo il concetto di potenza.
La potenza elettrica
La potenza degli apparecchi elettrici dipende dalla rapidità con cui l’apparecchio è in grado di funzionare; in particolare, si parla di potenza dissipata dal resistore in riferimento alla rapidità con cui l’energia elettrica è trasformata in energia interna.
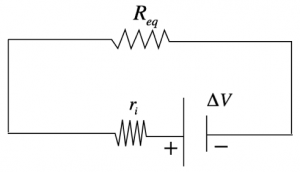
Consideriamo un dispositivo all’interno del quale sia presente un circuito elettrico attraversato da una corrente di intensità i, mantenuta da un generatore di corrente che crea una differenza di potenziale V. La potenza che si sviluppa all’interno del circuito è data dal prodotto di i per V:
$ P = i * V$
La formula precedente è valida per qualsiasi tipo di circuito, e qualsiasi tipo di conduttore.
Nel caso di conduttori ohmici, applicando la prima legge di Ohm, troviamo che la potenza dissipata è direttamente proporzionale alla resistenza del resistore, e al quadrato dell’intensità si corrente; si ha, quindi, la seguente relazione:
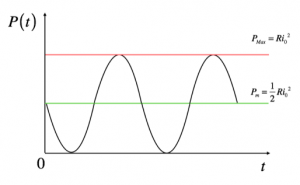
$ P = R * i^2$
Come abbiamo accennato precedentemente, vediamo con un altro tipo di ragionamento come la potenza che si sviluppa all’interno di un circuito può essere utilizzata per aumentare la temperatura del filo conduttore; partiamo dal fatto che la definizione di potenza ci dice che essa corrisponde al lavoro svolto nell’unità di tempo.
Dagli esperimenti di Joule, fu possibile dedurre che il lavoro e il calore sono de modi per esprimere scambi o trasformazioni di energia. Il calore, come sappiamo, è anch’esso una forma di energia; di conseguenza, è facile supporre che la potenza immagazzinata all’interno di un circuito, non potendo essere sfruttata per compiere lavoro meccanico, viene trasformata in calore.
Dato che un aumento di calore comporta un aumento di temperatura, si conclude che il passaggio di corrente all’interno di un conduttore aumenta la temperatura di esso.
La potenza di esprime in watt (W), mentre l’energia che viene assorbita da un dispositivo elettrico per il so funzionamento si esprime in Kilowattora (kWh); in particolare, 1 kWh corrisponde all’energia assorbita in un’ora da un dispositivo che dissipa la potenza di 1000W.
Applicazioni dell’effetto Joule
Vediamo ora alcuni esempi di apparecchi di uso quotidiano che sfruttano l’effetto Joule per il loro funzionamento.
- Alcuni tipi di lampadine, dette lampadine ad incandescenza, sono costituite da un involucro di vetro all’interno del quale, sotto vuoto, è posto un filo conduttore; la corrente che fluisce all’interno del filo provoca un forte aumento della temperatura di esso, fino a farlo diventare incandescente; questo permette, quindi, di illuminare l’ambiente circostante.
- Il forno elettrico presenta nella parte superiore un tubo conduttore, che serve per la funzione grill; grazie al passaggio di corrente, esso si riscalda fino a diventare incandescente, e riscaldare a sua volta lo spazio circostante. Il passaggio di calore per irraggiamento permette, quindi, la cottura degli alimenti.
- Alcuni tipi di piastre da cottura sfruttano la corrente elettrica per scaldare la propria superficie, cosicché sia possibile cucinare ponendo una pentola sopra di esse; in questo caso, il calore passa dalla piastra alla pentola per conduzione.
- Le stufe elettriche sfruttano l’effetto Joule per generare generare calore; questo calore viene poi trasmesso all’ambiente circostante per convezione, grazie alle correnti d’aria che la attraversano.
Potrebbero interessarti
Video Lezioni: Elettromagnetismo
Vide Lezioni: Onde e Luce
Appunti: Il teorema di Coulomb
Appunti: Il condensatore piano
Appunti: Condensatori in serie e in parallelo
Appunti: Energia immagazzinata in un condensatore
Appunti: La prima legge di Ohm e i resistori
Appunti: La corrente elettrica e i circuiti
Appunti: Risoluzione di un circuito
Appunti: La forza elettromotrice
Appunti: La conduzione elettrica nei metalli
Appunti: Processo di carica e scarica di un condensatore