Esiste in circolazione una gamma assai vasta di software specializzati nell'analisi statistica dei dati, basta ricordare SAS, SPSS, STATA, STATGRAPHICS PLUS, SHAZAM, S PLUS, MINITAB, GAUSS, etc., solo per citarne alcuni che sono in commercio.
Da alcuni anni a questa parte, soprattutto in ambito universitario (ma non solo) si sta sempre più diffondendo un nuovo package che costituisce anche una valida alternativa ai software sopraccitati: il software R.
La versione iniziale di R venne sviluppata per il sistema operativo MacOS da Ross Ihaka e Robert Gentelman del dipartimento di Statistica dell'Università di Auckland in Nuova Zelanda nel 1996. Successivamente altri ricercatori iniziarono ad aggiungersi e a fornire il loro contributo alla scrittura del codice sorgente e al miglioramento dell'applicazione, sviluppata in seguito anche per l'ambiente UNIX.
Nel 1997 è nato l'R Development Core Team, gruppo formato da statistici di tutto il mondo che si occupano dello sviluppo e della distribuzione del programma.
Successivamente è stata costituita dagli stessi membri dell'R Develpoment Core Team la R Foundation for Statistical Computing. Si tratta di una organizzazione non profit che lavora per il pubblico interesse allo scopo di promuovere lo sviluppo (attuale e futuro) e la diffusione del software e di interagire con la community che ruota intorno ad R, di gestire e tutelare il copyright di R e della relativa documentazione.
Nel 2004 si è svolta a Vienna la prima conferenza dedicata agli utilizzatori di R.

R è un ambiente statistico scaricabile gratuitamente da Internet sul sito di The R Project for Statistical Computing il cui indirizzo Internet è http://www.r-project.org1.
Esso è il frutto del lavoro collettivo svolto da un gruppo, sempre più folto, di ricercatori in campo statistico ed informatico a livello mondiale.
R più che un software statistico può essere definito come un ambiente, costituito da una varietà di strumenti, orientato alla gestione, all'analisi dei dati e alla produzione di grafici,
è basato sul linguaggio S creato da AT&T Bell Laboratories, ambiente dal quale è nato un altro software commerciale più noto, S-Plus, prodotto prima da MathSoft e ora da Insightful. A differenza di quest'ultimo, R è un GNU-Software, ossia è disponibile gratuitamente sotto i vincoli della GPL (General Public License).
Si tratta di un software opensource: chiunque può accedere al codice sorgente e modificarlo, migliorarlo, integrarlo e mettere a disposizione della comunità scientifica il proprio lavoro.
Inoltre è disponibile per diverse architetture hardware e sistemi operativi: Unix, Linux, Windows, MacOS. E' quello che tecnicamente si definisce un software multipiattaforma. Sul sito http://www.r-project.org è possibile scaricare, oltre che il programma base, anche
una serie di moduli aggiuntivi e un'ampia manualistica (in lingua inglese) sull'ambiente che va dall'installazione del software al suo utilizzo nell'analisi dei dati.

Le caratteristiche principali di R sono le seguenti:

• semplicità nella gestione e manipolazione dei dati;

• disponibilità di una suite di strumenti per calcoli su vettori, matrici ed altre operazioni complesse;

• accesso ad un vasto insieme di strumenti integrati per l'analisi statistica;

• produzione di numerose potenzialità grafiche particolarmente flessibili;

• possibilità di adoperare un vero e proprio linguaggio di programmazione orientato ad oggetti che consente l'uso di strutture condizionali e cicliche, nonché di funzioni create dall'utente.

R è un software opensource e ciò costituisce un suo punto di forza in quanto si ha la possibilità di accedere al codice sorgente e di modificarlo, ha un costo zero per l'utente finale il quale dispone di una vasta manualistica (in lingua inglese) consultabile e scaricabile da Internet. Inoltre è possibile accedere tramite Internet ad una vasta gamma di librerie per analisi statistiche molto dettagliate create e messe a disposizione di tutti da parte di ricercatori di tutto il pianeta. L'R Development Core Team supporta e assiste tutti gli utenti di R (una vera community a livello mondiale) grazie al sito Internet e alle liste di discussione tramite le quali ci si può avvalere dell'aiuto di esperti in statistica e informatica di tutto il pianeta.
R è un ambiente estremamente versatile: dà la possibilità di creare strumenti personali di analisi statistica ad hoc necessari per le proprie ricerche, ai quali si aggiungono strumenti di analisi statistica già pronti dai più elementari ai più sofisticati. Sono notevoli le possibilità grafiche e di programmazione rispetto ad altri software statistici.
R è dotato di una funzione di help in linea per ciascun comando facilmente richiamabile dal programma.
Tuttavia R presenta alcuni punti di debolezza trattandosi di un ambiente basato su un’interfaccia utente a carattere (CUI), anche se è possibile implementare un'interfaccia GUI (Graphical User Interface).C’è da considerare che le funzioni e le istruzioni vengono immesse da una linea di comando (command line interface), che pur essendo molto potente e semplice da usare, può mancare di alcune funzioni statistiche, inoltre la sintassi del linguaggio a volte risulta alquanto inconsistente. Benchè si tratti di un linguaggio ad alto livello, gli ideatori di R preferiscono presentarlo come linguaggio con cui lavorare in linea e non mediante l'esecuzione di programmi scritti su files. Non si comprende la ragione di tale scelta ma oggigiorno è comunque possibile scrivere programmi e farli eseguire nel modo familiare ai programmatori.
Esiste un’importante differenza a livello di filosofia tra R e la maggior parte degli altri packages statistici. Con gli altri software un'analisi statistica porta ad una grande quantità di output di informazioni e dati, mentre con R l’analisi statistica è condotta come una serie di passi, con risultati intermedi memorizzati in oggetti. Ad ogni passo dell’analisi gli output sono minimi e l’utente ha la possibilità di visualizzarli e manipolarli richiamando è necessario, gli oggetti nei quali i risultati dell'analisi sono contenuti.

L'ambiente R è basato sul concetto di "package" tradotto di solito in italiano con pacchetto. Un package è un insieme di strumenti che svolgono determinate funzioni, ma può anche contenere solo dati oppure solo documentazione.
Vengono di seguito esaminati sinteticamente i principali packages di R puntualizzando alcune delle funzionalità che questi consentono di operare.

1) Package "base": questo modulo è il motore dell'ambiente R, viene caricato automaticamente e fornisce all'utente gli strumenti per le più importanti e diffuse analisi statistiche come: ANOVA, regressione lineare, statistica descrittiva ed inferenziale, analisi esplorativa dei dati, grafici elementari, modelli lineari generalizzati, generazione di campioni delle più comuni variabili casuali, operazioni su matrici e vettori.

2) Package "ctest": consente di effettuare tutti i principali test statistici per la verifica delle ipotesi (test t, test F, test di normalità, test non parametrici, test per l'omoschedasticità delle varianze, test Chi-quadro, etc.).

3) Packages "ts" e "tseries": sono due packages dedicati all'analisi delle serie temporali.

4) Package "spatial": analisi dei dati di serie spaziali.

5) Packages "grid", "lattice", "rgl" e "scatterplot3d": permettono di realizzare e manipolare grafici avanzati e tridimensionali.

6) Packages "mva", "amap", "multidim" e "multiv": permettono di eseguire le principali analisi su dati multidimensionali (analisi delle componenti principali, analisi fattoriale, correlazione canonica, scaling multidimensionale, clustering gerarchico).

7) Package "cluster": è il modulo specializzato nell'analisi dei gruppi (cluster analysis).

8) Package "nls": effettua l'analisi della regressione con modelli non lineari applicando il metodo dei minimi quadrati (Nonlinear Least Squares).

9) Package "matrix": strumenti per l'uso avanzato di matrici e vettori con metodi numerici per l'algebra lineare.

10) Packages "survival" e "survrec": pacchetti specializzati nell'analisi della sopravvivenza.

11) Package "nlme": modelli lineari e non lineari con effetti misti (Linear and Nonlinear mixed effects models).

12) Package "foreign": contiene tutta una serie di funzioni utili per importare file da software statistici quali Minitab, S, SAS, SPSS, Stata.

I packages di cui sopra si ritiene che siano i più significativi e che abbraccino le più importanti e diffuse tipologie di analisi statistiche dei dati, sul sito del The Comprehensive R Archive Network – CRAN è possibile scaricare più di duecentocinquanta packages che spaziano nei più disparati campi della statistica applicata.

L’ambiente R è basato sul concetto di package, ovvero un insieme di strumenti che svolgono determinate funzioni. Attualmente è disponibile un’ampia gamma di pacchetti scaricabili dal sito http://cran.at.r-project.org/bin/windows/contrib e utilizzabili per analisi statistiche molto particolareggiate.
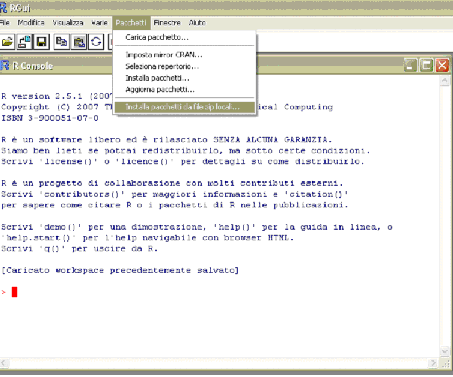
In particolare per l’analisi delle serie storiche, oltre ai pacchetti base e stats, ci si avvale dei pacchetti denominati tseries e ast. Possiamo installare tseries.zip in R tramite la voce di menù: Pacchetti – installa pacchetti da file zip locali. . . . Posizionarsi sulla directory dove è memorizzato tseries.zip e confermare con un doppio click :

 

 

Per caricare il package in R utilizzare il comando library (package = tseries) oppure require( package = tseries) dalla console. Un metodo alternativo consiste nello scegliere la voce Pacchetti – Carica pacchetto. . . dal menù a tendina.

 

 

 

Prima di poter iniziare l’analisi della serie storica occorre caricare i dati da una sorgente esterna, nel nostro caso un file di testo, specificandone nome e collocazione esatta. Se nel file è indicato il nome della variabile viene impostato il parametro header. Denominiamo la serie di dati x e per la lettura utilizziamo la funzione read.table():

 

> x<-read.table("C:/Documents and Settings/Giuseppe/Desktop/importazioni di energia extra ue.txt",header=TRUE)

 

In questo modo è stato creato un oggetto, denominato x, che R interpreta come un dataset con tre diverse variabili che abbiamo etichettato "anno", "mese" e "indice".
Se, ad esempio, si vuole esaminare la colonna di dati relativa al valore delle importazioni  e che abbiamo denominato indice, si digita:
 
> indice<-x\$indice

Il calcolo di alcune misure di sintesi rende maggiormente chiara la struttura della distribuzione della serie storica in esame, in particolare sono stati calcolati i seguenti indici:

> max(indice)
[1] 5239.805
> min(indice)
[1] 850.6836
> mean(indice)
[1] 2112.766
> var(indice)
[1] 1251893
> length(indice)
[1] 170

Affinchè l’oggetto indice venga riconosciuto come serie storica xt viene utilizzata la funzione ts()

> xt<-ts(indice,start=c(1993,1),frequency=12)

dove il primo parametro indica la sorgente, il secondo indica la data di partenza, il terzo indica la cadenza che nel nostro caso è mensile.
Si verifichi che il riconoscimento sia stato effettuato:

> is.ts(xt)
[1] TRUE

e si visualizzino i dati:

> xt

Per l’analisi grafica della serie storica si utilizza il comando plot()

> plot(xt,ylab="importazioni di enegia",xlab="tempo",main="GRAFICO DELLA SERIE STORICA",lwd=1,lty=1,col="red")

dove:

• il primo argomento è la serie di cui si intende fornire la rappresentazione grafica;

• ylab e xlab sono le etichette che si vuole compaiano sull’asse y e sull’asse x, rispettivamente;

• main specifica l’intestazione principale del grafico;

• lwd è il parametro che determina lo spessore della linea con cui si traccia il grafico;

• lty specifica il tipo di segmento con cui si intendono unire i punti successivi di una serie;

• col identifica il colore con cui si vuole venga tratteggiato il grafico.

Dalla rappresentazione grafica si rileva che la serie storica in esame è caratterizzata da un trend crescente, il quale risulta soprattutto evidente nei periodi intercorrenti tra novembre del 1998 e marzo del 2000 e tra gennaio 2003 e maggio 2006. E’ soprattutto in questo periodo che le importazioni di energia raggiungono picco massimo. Dal diagramma cartesiano si evince che la serie storica non è stazionaria.
Al fine di descrivere importanti aspetti della variabile in esame viene preso in considerazione l’istogramma:

> hist(indice,prob=TRUE,col="yellow")

La distribuzione di frequenza è asimmetrica positiva, in quanto il grafico è caratterizzato prevalentemente da una coda verso destra, presentandosi allungato verso il semiasse positivo delle ascisse.

 

 

 

 

 

 

 

Nell'approccio classico delle serie storiche si assume che i valori rilevati siano il risultato del comportamento congiunto di più componenti elementari individuabili attraverso opportune tecniche. A tale approccio sono state mosse numerose critiche, dal momento che non sempre risulta immediato individuare le componenti elementari e fornirne un'interpretazione. 

Lo scopo dell’analisi classica delle serie temporali è quindi quello di scomporre la serie nelle sue componenti elementari per poterle studiare meglio.
Le componenti di una serie storica di solito sono le seguenti: trend, stagionalità, ciclicità, residuale. Esse possono essere legate tra loro in modo additivo:

 Yt=Tt + St + Ct + Et,

dove le componenti sono espresse in termini assoluti, oppure in modo moltiplicativo:

Yt=Tt * St * Ct * Et,

in cui il trend Tt è espresso in termini assoluti, mentre le altre componenti sono espresse come fattore di proporzionalità rispetto a Tt.

La componente trend definisce l’andamento di lungo periodo della variabile e può essere definita come quella tendenza a crescere, a decrescere o a rimanere costante che un fenomeno manifesta in un lungo arco di tempo. La componente stagionale riguarda le dinamiche temporali con fase, periodo e ampiezza fissa tipica di serie storiche infrannuali, mentre il ciclo è tipico di serie storiche che descrivono fenomeni economici in un periodo di osservazione piuttosto lungo. La componente residuale racchiude fattori di natura erratica che influenzano il fenomeno in maniera casuale.
Per proseguire nell’analisi con R occorre implementare il pacchetto ast:

> "library(ast)"
[1] "library(ast)"

 

Stima delle componenti: Metodo delle medie mobili

Per la stima della componente trend i metodi più utilizzati sono: la perequazione meccanica con medie mobili e l’applicazione dell’operatore differenza.

Il metodo delle medie mobili consente di individuare l'andamento di lungo periodo della serie, eliminando l'influenza delle variazioni di breve periodo. Occorre determinare in maniera esatta il numero dei termini da perequare. Il pacchetto ast mette a disposizione la funzione filter():

> xt.filt<-filter(xt,filter=rep(1/25,25))

il parametro filter viene fissato al valore corrispondente ad una serie mensile.
Si visualizzi la serie storica depurata:

> xt.filt

E' stata applicata ai dati originari una media mobile ponderata a 13 termini per eliminare la stagionalità e mettere in risalto solo la componente di fondo. Per ottenere una visualizzazione grafica:

> plot(xt.filt,main="TREND STIMATO CON MEDIA MOBILE",col="green")

 

Metodo delle differenze

Un ulteriore metodo per eliminare il trend è quello di operare sulle differenze tra i termini della serie storica: le differenze del primo ordine rimuovono un trend lineare, quelle del secondo ordine un trend parabolico, quelle di ordine k rimuovono un trend polinomiale di grado k.
Il comando di R per applicare tale metodo è diff.ts()

> xt.diff<-diff.ts(xt)

Si visualizzi la serie storica differenziata

> xt.diff

Si riporta il grafico della serie storica detrendizzata:

> plot(xt.diff,main="GRAFICO DELLA SERIE STORICA DETRENDIZZATA",col="brown")

Usando in maniera ripetuta il comando diff.ts() si ottengono le differenze di qualsiasi ordine. Ad esempio la differenziazione del secondo ordine porta ai seguenti risultati:

> xt.diff2<-diff.ts(xt.diff)
> plot(xt.diff2,main="GRAFICA DELLA SERIE STORICA DETRENDIZZATA 2",col="brown")

 

 

 

 

 

Il livellamento esponenziale è un metodo che può aiutare a descrivere l’andamento di una serie storica e ad effettuare delle previsioni.
Il package stats mette a disposizione la funzione HoltWinters():

> xt.hw<-HoltWinters(xt,seasonal="additive")
> xt.hw
Holt-Winters exponential smoothing with trend and additive seasonal component.

Call:
 HoltWinters(x = xt, seasonal = "additive")

Smoothing parameters:
 alpha:    0.7442939
 beta :     0.001302468
 gamma:  0.92714

Coefficients:
             [,1]
a     4310.68335
b     11.50438
s1    142.07415
s2    -19.69130
s3    -28.46776
s4    -181.30670
s5    89.77291
s6    240.33962
s7    -174.54301
s8    97.76508
s9    135.58889
s10  164.81746
s11  195.66727
s12  -83.00070

Il grafico è il seguente:

> plot(xt.hw)

Se vogliamo effettuare la previsione dei volumi di energia negoziati nei successivi 5 mesi impieghiamo il metodo predict():

> prev<-predict(xt.hw,n.ahead=5)
> prev
                 Mar          Apr         May          Jun            Jul
2007   4464.262   4314.001   4316.729   4175.394   4457.978

Avendo a disposizione i dati reali, è possibile effettuare un confronto con le previsioni:

Marzo 2007     4544.019689
Aprile 2007     4402.56748 
Maggio 2007   4251.437933
Giugno 2007   4346.809605
Luglio 2007     4817.961483

Pur non trattandosi di una previsione raffinata, approssima l’andamento crescente della serie nel tempo.

 

L’approccio più semplice della decomposizione classica è basata sul modello di tipo additivo:
Yt= Tt + St + εt
con εt ~ NID (0,σ²) ovvero supponendo che gli errori siano distribuiti normalmente con media zero e varianza costante e siano tra loro indipendenti. Tali ipotesi saranno verificate tramite appositi tests di specificazione del modello. R consente di determinare e stimare tali componenti con tre diverse funzioni: decompose() e stl() nel package stats, tsr() nel package ast.

 

Funzione decompose

La funzione decompose() può essere applicata sia al modello additivo che al modello moltiplicativo, per questo occorre specificarlo nel parametro type=c(“additive”, “multiplicative”).

> dec.fit<-decompose(xt,type="additive")

La funzione restituisce un oggetto con le seguenti componenti:

• seasonal, vettore con la stagionalità

• figure, stima della componente stagionale per i dodici mesi dell’anno

• trend, vettore con il trend della serie

• random, vettore con gli errori.

Si memorizzino in alcuni vettori le tre componenti ottenute:

> stag.dec<-dec.fit$seasonal
> trend.dec<-dec.fit$trend
> res.dec<-dec.fit$random

Per ottenere il grafico della decomposizione della serie:

> plot(dec.fit)

 

Funzione stl()

La funzione stl() fornisce delle stime migliori in quanto per la decomposizione usa il metodo loess:

> stl.fit<-stl(xt,s.window="periodic")
> attributes(stl.fit)
$names
[1] "time.series" "weights"     "call"        "win"         "deg"        "jump"        "inner"       "outer"

$class
[1] "stl"

La funzione restituisce un oggetto le cui componenti possono essere memorizzate in vettori

> stag.stl<-stl.fit$time.series[,1]
> trend.stl<-stl.fit$time.series[,2]
> res.stl<-stl.fit$time.series[,3]

Il grafico della serie storica decomposta è il seguente

> plot(stl.fit,main="GRAFICO DELLA SERIE STORICA DECOMPOSTA- funzione stl")

 

Funzione tsr()

Si tratta di un’ulteriore funzione per la decomposizione di una serie temporale. Gli stimatori, detti smoothers, riconosciuti sono:

• constant: la serie assume valore uguale alla media;

• poly(r): la serie viene interpolata con un polinomio di grado r;

• loess(r, g): la serie viene stimata utilizzando una regressione locale di tipo loess;

• gauss(r, g): la serie viene stimata utilizzando una regressione locale con pesi gaussiani;

• spline(g): la serie osservata è stimata utilizzando una spline con g parametri equivalenti.

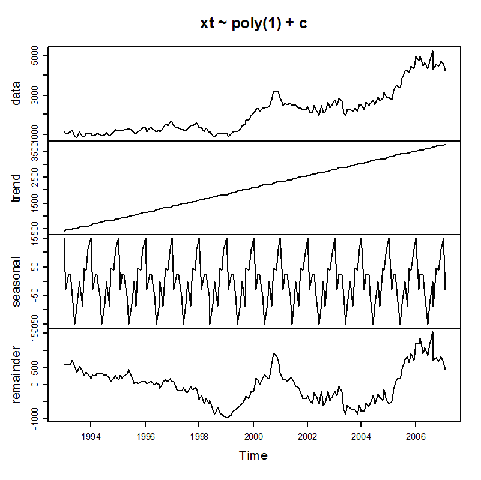
> tsr.fit<-tsr(xt~poly(1)+c)

Per avere una visualizzazione grafica del modello stimato:

> plot(tsr.fit)

Si valuti il grado di adattamento di questo tipo di trend tracciando il grafico della serie filtrata sovrapposto al trend stimato con tsr():

> plot(xt.filt)
> lines(trend(tsr.fit),col="red")

Come si può facilmente vedere l’adattamento non è particolarmente buono e ciò induce all’utilizzo di un altro tipo di stimatore, ad esempio di tipo loess:

> tsr2.fit<-tsr(xt~loess(1,10)+c)
> plot(tsr2.fit)

Si valuti il grado di adattamento:

> plot(xt.filt)
> lines(trend(tsr2.fit),col="blue")

Il risultato è decisamente migliore. Per determinare il numero dei parametri spesso si deve procedere per tentativi, ma in generale aumentando il numero dei parametri equivalenti il grado di adattamento migliora.
Si confrontino i trend stimati con i tre metodi:

> plot(trend(tsr2.fit),main="COMPARAZIONE DEL TREND STIMATO")
> lines(xt.filt,col="red")
> lines(trend.stl,col="green")

Si proceda alla memorizzazione delle componenti risultanti dalla funzione tsr() in tre vettori distinti

> trend.tsr<-trend(tsr2.fit)
> stag.tsr<-seasonal(tsr2.fit)
> res.tsr<-residuals(tsr2.fit)

 

 

 

 

 

 

 

 

 

 

 

 

 

La funzione smoothts() del package ast permette di “lisciare” una serie temporale in una varietà di modi attraverso l’impiego degli stessi stimatori visti per la funzione tsr().
Di seguito è riportato il grafico di una serie di “lisciamenti” della serie storica delle importazioni di energia:

> plot(xt,main="LISCIAMENTO DELLA SERIE STORICA")
> lines(smoothts(xt~lo(2,10)),col="red")
> lines(smoothts(xt~s(2)),col="blue")
> lines(smoothts(xt~p(2)),col="black")

 

 

 

Depurando i valori della serie in esame dalle componenti trend e stagionale, si ottiene la componente accidentale o casuale. Si suppone che tale componente residuale si distribuisca come una normale con media pari a zero, varianza costante e che non vi sia autocorrelazione. Tali ipotesi alla base del modello devono essere verificate con opportuni test statistici detti test di specificazione del modello. Il venir meno di una di queste ipotesi potrebbe inficiare la validità del modello adottato.
Si verifichi che la media dei residui non sia significativamente diversa da zero mediante il test t. Possono essere considerati i residui stimati con uno dei tre metodi di decomposizione precedentemente analizzati. Consideriamo quelli ottenuti con la funzione stl(): res.stl().
Si calcoli la media dei residui:

> media.residui<-mean(res.stl)
> media.residui
[1] 0.6746644

viene calcolato il numero di osservazioni presenti nella serie:

> n<-length(res.stl)
> n
[1] 170

vengono inoltre calcolati la varianza corretta e lo scarto quadratico medio:

> var.residui<-(n/(n-1))*var(res.stl)
> var.residui
[1] 21741.79
> s<-sqrt(var.residui)
> s
[1] 147.4510

Si può a questo punto determinare il valore del test t:

> test<-(media.residui/(s/sqrt(n)))
> test.t
[1] -0.01869310

il cui p-value è

> pt(test.t,n-1,lower.tail=F)
[1] 0.507446

oppure considerando il valore soglia del test ad un livello di significatività del 99%

> qt(0.99,n-1)
[1] 2.348615

ciò ci consente di concludere che la media degli errori non è significativamente diversa da zero.

Per verificare che i residui si distribuiscano effettivamente secondo una variabile aleatoria normale, occorre preliminarmente individuare e rimuovere i valori anomali presenti. È preferibile operare sui residui standardizzati in quanto numeri puri:

> stand<-function(x){m=mean(x)
+ s=(var(x)^0.5)
+ z=(x-m)/s
+ return(z)}

Si crei il vettore dei residui standardizzati:

> res.stand<-stand(res.stl)
> res.stand

e se ne tracci il grafico:

> plot(res.stand,main="DIAGRAMMA DEI RESIDUI STANDARDIZZATI")
> abline(h=2.5)

Dal diagramma emerge che solo due osservazioni risultano essere anomale poiché si trovano al di là della banda di confidenza del 99% ( banda compresa tra -2,5 e 2,5). Si può ragionevolmente supporre che la causa risieda in fattori o eventi di natura episodica.

Un modo abbastanza semplice ed intuitivo per verificare la normalità della distribuzione degli errori è quello di ricorrere ad un ausilio grafico:

> hist(res.stand,main="ISTOGRAMMA DEI RESIDUI STANDARDIZZATI",xlab="Residui",col="green")

> plot(density(res.stand,kernel="gaussian"),main="Distribuzione dei residui:lisciamento",col="green")

Entrambi i grafici ci danno una buona indicazione per una probabile distribuzione normale dei residui. Per avere un risultato più affidabile bisogna effettuare ulteriori test, in particolare si ricorre al test di Wilk – Shapiro.

 

 

 

 

 

Il test di Shapiro-Wilk è considerato in letteratura uno dei test più potenti per la verifica della normalità, soprattutto per piccoli campioni.
La verifica della normalità avviene confrontando due stimatori alternativi della varianza σ²: uno stimatore non parametrico basato sulla combinazione lineare ottimale della statistica d'ordine di una variabile aleatoria normale al numeratore, e il consueto stimatore parametrico, ossia la varianza campionaria, al denominatore. I pesi per la combinazione lineare sono disponibili su apposite tavole. La statistica W può essere interpretata come il quadrato del coefficiente di correlazione in un diagramma quantile-quantile.
Il comando per effettuare il test di normalità in questione in ambiente R è shapiro.test() presente nel package stats. Esso restituisce come risultato il valore della statistica W e il relativo p-value:

> shapiro.test(res.stand)

        Shapiro-Wilk normality test

data:  res.stand
W = 0.9585, p-value = 6.164e-05

Il p-value è elevato rispetto ai livelli di significatività a cui di solito si fa riferimento: ciò fa propendere per l’ipotesi nulla ovvero la normalità della distribuzione degli errori.

Si può avere un fenomeno di autocorrelazione temporale, a causa dell'inerzia o stabilità dei valori osservati, per cui ogni valore è influenzato da quello precedente e determina in parte rilevante quello successivo.
Esistono diversi test statistici per saggiare la presenza di una correlazione seriale dei residui di una serie storica.

Uso del correlogramma

Un modo abbastanza semplice per vedere se una serie presenza autocorrelazione è quella di tracciarne il correlogramma con la funzione acf(). In caso di assenza di autocorrelazione la distribuzione asintotica della stima del coefficiente di autocorrelazione è di tipo normale.

> acf(res.stand,main="Correlogramma dei residui",col="red")

Le linee tratteggiate di colore azzurro indicano la banda di confidenza ad un livello del 95%. Al variare del lag temporale i coefficienti di autocorrelazione dei residui risultano essere tutti interni alla banda di confidenza, indicando quindi assenza di correlazione serie.

 

L’approccio moderno o stocastico (contrapposto a quello classico o deterministico) si basa sul concetto mutuato dal calcolo delle probabilità di processo stocastico.
Definiamo il processo stocastico come una famiglia (o successione) di variabili aleatorie X_t(W) definite sullo stesso spazio degli eventi W e ordinate secondo un parametro t (appartenente allo spazio parametrico T) che nell’analisi delle serie storiche è il tempo. In questo modo la serie storica può considerarsi come una
realizzazione campionaria finita del processo stocastico.
Applichiamo questi concetti alla serie dei residui standardizzati stimati con il metodo stl() contenuti nel vettore res.stl. Stimiamo media e varianza del processo:

> mean(res.stl)
[1] 0.6746644
> var(res.stl)
[1] 21613.9 

Per quanto riguarda le funzioni di autocovarianza e di autocorrelazione si usa il comando acf() che permette di ottenere il correlogramma o il grafico delle autocovarinaze oppure la semplice stampa delle autocovarianze o dei coefficienti di autocorrelazione:

> acf(res.stl,type="correlation",plot=TRUE,main="CORRELOGRAMMA DELLA SERIE DEI RESIDUI",col="violet")

> acf(res.stl,type="covariance",plot=TRUE,main="GRAFICO DELLE AUTOCOVARIANZE",col="orange")

I principali argomenti di acf(), oltre alla serie storica, sono type, con il quale ci specifica se si vogliono calcolare le autocovarianze (type=”covariance”) o i coefficienti di correlazione type=”correlation”) e plot che serve per indicare se tracciare il grafico (plot=TRUE) che è il valore di default oppure se stampare l’output (plot=FALSE)

> acf(res.stl,type="correlation",plot=FALSE)

Autocorrelations of series 'res.stl', by lag

0.0000 0.0833 0.1667 0.2500 0.3333 0.4167 0.5000 0.5833 0.6667 0.7500 0.8333
 1.000  0.251 -0.007 -0.087 -0.204 -0.026 -0.030 -0.077  0.004  0.134  0.042
0.9167 1.0000 1.0833 1.1667 1.2500 1.3333 1.4167 1.5000 1.5833 1.6667 1.7500
 0.029 -0.046 -0.242 -0.135 -0.027  0.004  0.033 -0.038  0.080  0.118 -0.040
1.8333
-0.156
 

che fornisce i lag e i corrispondenti coefficienti di autocorrelazione o le autocovarianze. Con il comando acf() è possibile stimare anche i coefficienti di correlazione parziale specificando l’argomento type=”partial”. Analogo risultato si ottiene con il comando pacf().
La correlazione ρ(k) tra dati distanti k lag è influenzata dalle relazioni lineari con i dati intermedi. La funzione di autocorrelazione parziale p(k) misura la correlazione tra x_t e x_t+k dopo che sia stata eliminata la parte “spiegabile linearmente” da x_t+1, x_t+2, . . . , x_t+k-1 .

> pacf(res.stl,plot=TRUE,main="GRAFICO DELLE CORRELAZIONI PARZIALI",col="green")

> pacf(res.stl,plot=FALSE)

Partial autocorrelations of series 'res.stl', by lag

0.0833 0.1667 0.2500 0.3333 0.4167 0.5000 0.5833 0.6667 0.7500 0.8333 0.9167
 0.251 -0.075 -0.071 -0.177  0.071 -0.064 -0.085  0.009  0.149 -0.059  0.010
1.0000 1.0833 1.1667 1.2500 1.3333 1.4167 1.5000 1.5833 1.6667 1.7500 1.8333
-0.042 -0.194 -0.057  0.020 -0.018 -0.062 -0.076  0.124  0.027 -0.125 -0.105

I processi AUTOREGRESSIVI

Sia {Z_t, t $\in$ T}, sia ε_t un processo white noise WN(0, σ²), allora:

Z_t=Φ_tZ_t-1+ε_t

rappresenta un processo autoregressivo del primo ordine AR(1);

Z_t=Φ₁Z_t-1+Φ₂Z_t-2+ε_t

rappresenta un processo autoregressivo del secondo ordine AR(2);

Z_t=Φ₁Z_t-1+Φ₂Z_t-2+…+Φ_pZ_t-p+ε_t

rappresenta un processo autoregressivo del generico ordine p AR(p), dove Φ₁,Φ₂,…,Φ_p  sono i parametri del modello AR da stimare. Tali processi sono stazionari solo se i parametri soddisfano determinate condizioni, ovvero sono in modulo maggiori di 1. Di solito si suppone che la variabile di white noise sia di tipo gaussiano al fine di stimare i parametri in base al metodo della massima verosimiglianza.

I processi MOVING AVERAGE

Sia {Z_t, t $\in$ T}, sia a_t un processo white noise WN(0, σ²), allora:

Z_t=a_t-θa_t-1

rappresenta un processo a media mobile del primo ordine MA(1);

Z_t=a_t-θ₁a_t-1-θ₂a_t-2

rappresenta un processo a media mobile del secondo ordine MA(2);

Z_t=a_t-θ₁a_t-1-θ₂a_t-2-…-θ_qa_t-q

rappresenta un processo a media mobile del generico ordine q, dove θ₁, θ₂,…,θq sono i parametri del modello MA da stimare. Tali processi sono sempre stazionari. Di solito si suppone che la variabile di white noise sia di tipo gaussiano al fine di stimare i parametri in base al metodo della massima verosimiglianza.

I processi ARMA

Un processo ARMA è dato dalla combinazione tra un processo AR(p) e un processo MA(q): 

Z_t=Φ₁Z_t-1+Φ₂Z_t-2+…+Φ_pZ_t-p+a_t-θ₁a_t-1-θ₂a_t-2-…-θ_qa_t-q,

Z ~ ARMA(p, q)  è un processo autoregressivo media mobile di ordine (p,q), dove Φ₁, Φ₂,…,Φ_p e θ₁, θ₂,…,θ_q sono i parametri del processo ARMA da stimare. Il processi ARMA sono stazionari solo se si verificano alcune condizioni.

 

I modelli ARIMA (autoregressivi integrati a media mobile ) di Box e Jenkins partono dal presupposto che fra due osservazioni di una serie quello che altera il livello della serie è il cosiddetto disturbo. Un modello generale di Box-Jenkins viene indicato come: ARIMA (p,d,q) dove AR=AutoRegression (autoregressione) e p è l’ordine della stessa, I=Integration (integrazione) e d è l’ordine della stessa, MA=Moving Average (media mobile) e q è l’ordine delle stessa.
Pertanto un modello ARIMA (p,d,q) è analogo ad un modello ARMA(p,q) applicato alle differenze d'ordine "d" della serie dei valori, invece che agli effettivi valori. Se la serie non è stazionaria (la media e la varianza non sono costanti nel tempo) viene integrata a livello 1 o 2, dopo aver eseguito un' eventuale trasformazione dei dati (solitamente quella logaritmica). In tal modo viene ottenuta una serie stazionaria (random walk).
La procedura proposta Box e Jenkins è di tipo iterativo e serve per: l’identificazione, la stima e la verifica di un modello ARIMA ed ha come scopo la costruzione di un modello che si adatti alla serie storica osservata e che rappresenti il processo generatore della serie stessa.

1) Verifica della stazionarietà della serie: analisi grafica della serie; identificazione di eventuali valori anomali; ricerca delle trasformazioni più adeguate a rendere stazionaria la serie (calcolo delle differenze e uso della trasformazione Box-Cox);

2) Identificazione del modello ARIMA: individuazione degli ordine p,d,q del modello mediante l’analisi delle funzioni di autocorrelazione parziale e totale;

3) Stima dei parametri: stima dei parametri del modello ARIMA con il metodo della massima verosimiglianza o dei minimi quadrati;

4) Verifica del modello: controllo sui residui del modello stimato per verificare se sono una realizzazione camponaria di un processo white noise a componenti gaussiane. Si effettuano analisi dei residui, test sui coefficienti, cancellazione fra operatori, test Portmanteau.

Se il modello stimato supera la fase di verifica allora può essere usato per la scomposizione e/o le previsioni. Altrimenti si ripetono le fasi di identificazione, stima e verifica (procedura iterativa).
Per quanto riguarda la stima dei parametri dei processi stocastici R mette a disposizione alcune funzioni che ora esaminiamo. Il comando arima.sim() permette di ottenere la simulazione di modelli AR, MA, ARMA, ARIMA specificando il numero dei valori che si vogliono ottenere, i parametri e/o l’ordine del modello in una lista.

Processo AR 

Si proceda per tentativi per l’individuazione del modello che meglio approssima i dati.

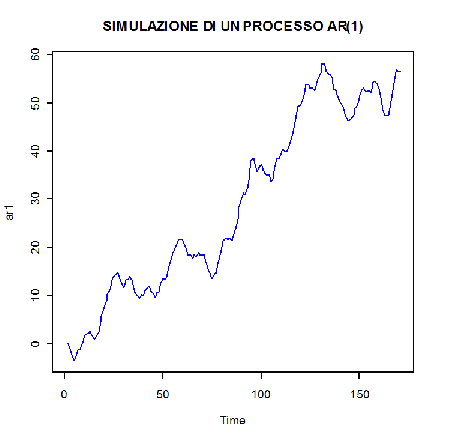
•  Simulazione di in modello AR(1) di 170 osservazioni fissando il parametro phi=0.6

> ar1<-arima.sim(n=170,list(order=c(1,1,0),ar=0.6))
> ar1
Time Series:
Start = 1
End = 171
Frequency = 1
  [1]  0.0000000 -0.7375444 -1.0355689 -2.4777613 -3.2032724 -2.2948103
  [7] -1.4941182  0.1368093  1.3850390  1.6277919  4.3641105  6.8016733
[13]  8.2328860  9.0499250 10.7308301 12.2702634 14.9032258 16.4995706
[19] 19.4134018 19.8904482 21.8807648 24.6778776 24.9983011 24.6157512
[25] 24.9478638 24.1727737 23.2579988 23.0778887 23.4324396 25.4085608
[31] 27.5649249 30.6109207 33.8436144 35.9743635 37.0941200 38.1313182
[37] 39.3090742 38.3976588 37.9543105 37.9500902 37.1770428 34.8367185
[43] 33.2934830 33.1244562 33.8171131 33.1678666 32.1401018 31.6099869
[49] 32.1591811 32.1303764 32.1486393 32.0200748 31.8405200 30.7802915
[55] 30.1212859 30.2690738 29.9777318 29.7323914 28.1452512 26.7055688
[61] 25.2828056 24.2621105 23.5874187 23.9320366 23.5284242 23.3078160
[67] 22.5596057 23.9519282 25.4960161 25.8549445 26.4484951 27.4126224
[73] 27.4243587 28.5075360 30.4841291 32.4843120 33.6289029 35.4467279
[79] 37.1227387 37.9812208 39.4522379 40.0379323 41.4059387 43.0711273
[85] 43.1771526 42.6844963 42.2212529 42.6927428 43.2140957 44.6267419
[91] 46.4059593 45.5815914 47.7594108 49.5538808 51.3366225 53.2515319
[97] 54.0200389 54.3239880 52.1873142 49.4323891 48.2891544 46.7765355
[103] 46.2690071 47.8717656 49.1076176 50.0322755 49.8788161 49.0825702
[109] 48.5961916 47.0287084 46.7841064 43.7322763 42.0717208 39.1940967
[115] 38.6412168 39.2892602 39.0265183 40.1082926 41.2851121 41.9517134
[121] 42.3389658 42.6226749 41.2378144 41.7813225 43.8046498 45.1969681
[127] 46.3753271 46.3818114 45.7429408 44.8397104 45.7706242 45.8623730
[133] 46.6183370 46.0031969 45.7647150 44.9246292 44.4294642 44.4562933
[139] 44.1665859 44.3390046 44.0077456 44.9850511 45.5315941 45.4270736
[145] 45.5421237 46.4077095 46.0270904 44.6091774 44.1203040 43.9732206
[151] 43.4359909 42.4899423 40.6917906 39.8144287 40.0876248 42.2593350
[157] 43.3158349 45.2563954 46.4372344 48.8340793 49.8591207 50.4734704
[163] 51.2639939 52.8132332 51.3220445 50.1243572 49.7937006 50.0489639
[169] 48.3752694 46.4184937 45.4417512

> plot(ar1,main="SIMULAZIONE DI UN PROCESSO AR(1)",col="blue")

 

• Simulazione di un modello AR(1) di 170 osservazioni con parametro phi=0,15 e varianza 2,5:

> ar11<-arima.sim(n=170,list(ar=0.15,sd=sqrt(2.5)))
> ar11
Time Series:
Start = 1
End = 170
Frequency = 1
  [1] -1.4690336339 -0.0399395037  0.2998336591  1.2594775188
  0.1904448332
  [6]  1.0639445584  0.6947342595  0.7701135951  0.1826711094
  1.7597503216
[11] -0.9733798050 -1.2010013969 -0.1916544802  0.4634392155
  0.9031037004
[16]  2.4568212842 -0.6093219668  1.9675608364 -0.1324824978
-0.0732688324
[21]  0.9868222490  0.3652817330  0.8078136447 -1.7991087165
-0.4428696191
[26] -1.7447511838  0.4147847593 -1.4708191643  1.4685543918
-1.7646362786
[31] -0.3736421355  1.7725704051  0.7833342347  0.0006343414
  1.7357028453
[36]  0.7060314166 -0.4008795948 -1.1539233745  2.6666979960
-0.3564715486
[41]  0.2194268785  0.7804850920 -0.4620249576 -1.3175543274
  0.3021856521
[46]  0.3230394955  1.7472424366  1.0308000046  1.4012097760
  0.3416421527
[51]  0.4653618897  2.5764826993  1.6142970771 -0.5480520514
-1.1827095500
[56]  1.0949808309  0.5344900767 -0.3636353290  1.2727688493
-0.0068179214
[61]  1.3514429741 -0.7982123924  0.5779981685 -0.1145635273
  2.0335351457
[66] -0.1007232829  0.7895741837 -1.0775374813 -1.9429762364
-1.1080397179
[71] -0.9554619634  0.1772038499 -1.0474989050 -0.7183051153
-0.4335751750
[76] -0.9247199904 -0.4278831220 -0.1958545391  0.2425973929
-1.1089011185
[81] -0.0196799632  0.0547540556  0.5909806813 -0.5648335499
-1.6485220027
[86]  0.7893906276 -0.0493015621 -2.8409610477 -1.0042187144
-0.3527099945
[91] -1.6315823695 -0.2596377325 -0.9965897859 -1.5074801631
-2.8388178062
[96] -1.1259776472 -0.0155683575 -0.0797057545 -0.7469027961
-0.8571402741
[101]  0.9465972978  0.0171989364 -1.0831551621 -2.3095084329
-0.8882108521
[106] -0.2176889819  0.9407394329  1.1565404638  0.4013548307
  0.1679217379
[111] -1.9434344806 -1.6067222890  0.8237059669  1.0845215838
  1.5100616922
[116] -0.7890057819 -0.5797764945  0.4267545410  0.7049636954
-0.2774157598
[121]  0.9242622818  0.2016104080 -0.1172035949  0.4629335735
-0.7848993341
[126]  1.5859457213 -0.0687890336  0.6622152044 -0.4653405760
  1.4280674917
[131]  0.4910126175 -0.9890212262  1.0714418193 -0.7121885739
-1.4813067180
[136] -1.1075278776  0.1961005034  0.7412216432 -0.3724257757
  0.3305613563
[141]  1.1629642958  0.3776128142  0.2423366461 -1.4777760402
-0.2484361533
[146] -0.1669756235  1.2881987699 -0.2368699130  0.4625279491
-2.0167793174
[151] -0.6785451036  1.8835828853  0.3859228748 -0.4253082996
-0.0739179005
[156] -0.3845038762  0.6340635332  0.1953291053  0.1834966665
-0.1570903562
[161] -1.3834511461 -0.6669976388 -0.7769142032 -0.6939895778
-0.9903816740
[166]  0.6223976876  0.4962423529 -0.2174298546 -1.5667120756
-0.0209512910

> plot(ar11,main="SIMULAZIONE DI UN PROCESSO AR(1)",col="brown")
> abline(h=2.5)
> abline(h=-2.5)

Il modello ar11 sembra bene adattarsi alla serie, tuttavia si tenta anche l’implementazione di un modello AR di ordine superiore al primo.

•  Simulazione di in modello AR(2) di 100 osservazioni con parametri phi1=0,5 e phi2=0,4

> ar2<-arima.sim(n=170,list(order=c(2,1,0),ar=c(0.5,0.4)))
> ar2
Time Series:
Start = 1
End = 171
Frequency = 1
  [1]   0.0000000   0.7416458   0.3408995   1.5255966   2.4866915 
3.6166142
  [7]   2.8964864   1.9531290   1.2535401  -0.8942762  -1.3884878
  -2.4389653
[13]  -4.2267933  -2.8160017  -2.5025175  -1.5966160  -3.9347968
  -4.2038814
[19]  -6.7303460  -8.1565659  -8.4282293  -9.2834039  -7.9099521
  -7.5129642
[25]  -6.5902404  -6.9066107  -5.7924841  -5.5600443  -6.3409236
  -5.9363999
[31]  -6.7870383  -9.0245331 -11.1512455 -12.4515057 -13.9602165
-15.5019754
[37] -18.2546020 -19.9257488 -22.0674941 -24.4675801 -27.2571622
-29.6364010
[43] -33.2228625 -36.7070816 -40.8920534 -44.0812366 -47.0841146
-51.5749387
[49] -54.5143933 -56.7928253 -58.2786986 -58.5026433 -59.2639845
-57.6444203
[55] -55.9213076 -53.9666046 -52.7702893 -53.3758109 -51.8470716
-50.7052869
[61] -48.7620241 -47.7043315 -47.1821508 -47.6432204 -47.3701677
-48.1909230
[67] -49.9738153 -51.5065356 -52.0038625 -54.4409229 -55.3404225
-54.8830192
[73] -53.4031546 -52.5725307 -51.2958713 -50.5414842 -48.6141725
-46.5231167
[79] -45.0802080 -44.9065231 -45.1604485 -43.6586001 -42.4579558
-40.5537259
[85] -39.2451215 -36.5794929 -34.6886051 -32.6218435 -29.3548277
-26.8210874
[91] -23.4517635 -20.9925591 -17.8160170 -14.8897997 -12.0038517
-10.6299223
[97]  -8.0423293  -5.8811788  -3.9416850  -2.0744492  -1.9024769
  -0.4065754
[103]   0.2941647  -1.0306816  -0.1901607  -0.1969264   0.7379729 
2.3615291
[109]   1.1770707   2.1314974   3.9981788   6.5822079   7.0730939
  10.0228340
[115]  10.1093402  11.3804773   9.9022800   8.2023428   6.6197507 
6.7794372
[121]   5.8105842   6.0151686   6.5614464   7.3748200   8.1897428 
7.2777576
[127]   8.1026103   8.5314157   8.7264903   8.2040121   6.4173916 
4.9390432
[133]   3.9165203   2.5899927   2.4310707   1.8668086   1.9251183 
3.2735172
[139]   3.6952221   4.9531544   4.7516738   6.0924070   7.0936590 
8.0631714
[145]   7.3917729   6.2365062   5.7605649   3.4207370   1.8813469
  -0.9456497
[151]  -4.1839871  -6.6217168  -9.8913829 -13.0697841 -15.7380008
-18.2078140
[157] -21.2155178 -24.4036006 -26.8389525 -30.6880774 -33.7792946
-37.0253318
[163] -40.3574752 -43.6375021 -46.0753507 -48.0424241 -50.5798501
-52.3177688
[169] -53.7696224 -53.4816007 -53.7934251

> plot(ar2,main="SIMULAZIONE DI UN PROCESSO AR(2)")

• Simulazione di in modello AR(2) di 170 osservazioni con parametri phi1=0,88 e phi2 = –0,49 e varianza 0,15:

> ar22<-arima.sim(n=170,list(ar=0.88,-0.49),sd=sqrt(0.15))
> ar22
Time Series:
Start = 1
End = 170
Frequency = 1
  [1] -0.964082056 -1.180453543 -1.015624773 -1.013722166 -0.661666691
  [6] -0.081283227 -0.263501226 -0.578210892 -0.723210881 -0.149671137
[11] -0.708030378 -0.657979077  0.246154370  1.171803934  1.058795999
[16]  1.080316342  1.426547869  1.326610476  0.820915839  0.088268315
[21]  0.077293721 -0.777979888 -1.251450707 -1.269327896 -0.952887575
[26] -1.198701600 -1.597272416 -1.194151138 -0.655575517  0.961026998
[31]  0.661587886  1.030530256  0.948983976  0.626951724  0.806586436
[36]  0.142302419  0.062779558  0.087133597 -0.564976087 -0.911341680
[41] -0.818683245  0.017327733  0.018787846 -0.008157721 -0.008874559
[46] -0.496787200 -0.830570116 -0.579240450 -0.619959592 -0.972678643
[51] -1.025915974 -0.547766278  0.447416637  0.954630066  0.760727393
[56]  1.025591399  0.886856437  0.019711354  0.316259694  0.075342631
[61]  0.548930794  0.918894012  1.126035291  1.374897711  1.797419208
[66]  1.194903784  0.865367572  0.523007728  0.865300788  0.119702341
[71] -0.194865199  0.198625090  0.038040353  0.180345284  0.350205061
[76]  0.258697287  0.101998130  0.137509044  0.871133580  0.720081558
[81]  1.173211283  1.076440877  0.925734339 -0.009027872 -0.093374467
[86] -0.242600797  0.102010438  0.240159758 -0.022964073  0.278776440
[91] -0.216898388 -0.888970862 -1.638354706 -0.957271575 -0.879533254
[96] -1.253929162 -0.817519384 -0.805693987 -0.113425826 -0.016256955
[101] -0.351257997 -0.326800000 -0.353918549 -0.420720032 -1.480320961
[106] -1.480968227 -1.136130864 -1.158153650 -0.526739981 -0.836083409
[111] -0.802566461 -0.284775013 -0.036024191 -0.182723308 -0.194359702
[116]  0.109151838  0.074321542  0.537275112  0.102677163  0.445787862
[121]  0.860511143  1.419628422  1.227569538  0.801330553 -0.222442338
[126]  0.192470694  0.289465044  0.127952137  0.099396279 -0.384897111
[131] -0.796878964  0.009275999  0.482795319  1.035156544  0.531234982
[136]  0.917589121  0.258871912  0.529330695  0.513471822  0.345772905
[141]  0.317033172  0.258317913 -0.368594758 -0.109077366 -0.134507556
[146] -0.481433641  0.199203218 -0.190775442 -0.342969155 -0.187695630
[151] -0.236342158  0.116273927 -0.003930588 -0.858844661 -0.857620380
[156] -0.831315624 -1.091812963 -0.453843713 -0.281395848  0.282293788
[161]  0.412911800  0.294513676  0.432096062  0.499506437  0.337337262
[166]  0.562179507  0.517949064  0.217866289  0.015743004  0.277508224

> plot(ar22,main="SIMULAZIONE DI UN PROCESSO AR(2)")
> abline(h=0.15)
> abline(h=-0.15)

 

Processo MA

• Simulazione di in modello MA(1) di 170 osservazioni con parametro theta=-0,7

> ma1<-arima.sim(n=170,list(order=c(0,1,1),ma=-0.7))
> ma1
Time Series:
Start = 1
End = 171
Frequency = 1
  [1]  0.00000000 -0.14537086  1.41001634  0.30581352  0.45762145
  1.47130453
  [7]  1.13395496  1.22709055  1.66558899  0.73830575  0.83026869
  0.44228278
 [13] -0.02017238  0.62654233 -0.51275444 -2.00369661 -1.16496636
 -0.26063591
 [19] -0.43824753 -0.97884216 -0.73318258 -0.54660170  0.09312164
 -1.47335054
 [25] -0.37722986 -1.35428552 -0.29277995 -0.53551190 -0.68125825
  0.79404591
 [31]  0.49757692  0.07500706 -0.31185477 -0.17634488 -0.61620559
  0.67859303
 [37]  0.51787649 -0.10001863 -0.32427306  1.12555164  0.80363636
  1.53676514
 [43]  0.77973908 -0.54330862 -0.98716267 -1.13386554 -1.48662789
 -1.52761709
 [49] -2.37229023 -0.80906902 -1.06510346  1.53887104  0.31189699
  0.49708015
 [55] -1.92002836  1.68350772  1.49330139  0.51873653 -0.11812353
  1.03284356
 [61] -0.11546888 -2.31227719 -3.16249789 -1.13884591 -1.82516761
 -2.11083163
 [67] -2.40910846 -3.21375919 -2.57729189 -1.28013568 -1.22331259
 -1.52700430
 [73] -0.64529645 -1.67102232  0.25920612 -0.65134642 -0.33858645
  0.81050832
 [79] -1.23940790 -0.97509553  1.03789187 -0.02563110 -0.87591974
 -1.90238138
 [85] -0.54331505  0.83173354  0.26578485  1.18406185 -0.63909376
 -1.24665254
 [91] -1.31467793  1.13527815  0.64509378  0.81633600  1.84856869
  0.97748616
 [97]  1.75803986  0.29104837 -0.43134955  0.24004645  0.55232638
 -1.31512735
[103] -3.07909811 -1.91233483 -0.61834732 -1.12493358 -1.03155155
 -0.33040522
[109] -0.59254922  0.08903392 -1.79445949  0.22735775 -0.36632314
 -0.83283235
[115] -0.54003661  0.11281521  0.30926505 -0.98179449 -0.28850550
 -0.20986720
[121] -1.02922818  0.12217547 -0.21905254  0.41799567 -1.14883208
 -0.55756252
[127] -0.59355013  0.47652730 -0.79747280 -0.56551155 -0.85614171
 -0.43184318
[133]  0.54386500  1.65162323  1.41972075  0.12959225  0.41476582
  1.21531679
[139]  1.29329107  1.72070785  0.57374928  0.85851370  0.68322633
 -0.95400487
[145] -0.23602644  0.46336938  0.29425772 -0.30474161  0.48087832
  0.49384372
[151] -0.63588359  0.45696279 -0.30923628  1.28298185  0.02806556
 -0.19737218
[157]  1.09644359 -0.08703303 -0.66437011  2.47805107  0.72490842
  0.48694640
[163]  1.85869255  1.97578221  2.03270994  2.82619735  2.82285238
  1.62191478
[169]  1.15720103  1.80676993  1.06868728

> plot(ma1,main="SIMULAZIONE DI UN PROCESSO MA(1)",col="yellow")

 

Processo ARIMA

• Simulazione di un processo ARIMA(1,1,1) con parametri AR=0,05 e MA=0,3

> arima1<-arima.sim(n=170,list(order=c(1,1,1),ar=0.05,ma=0.3))
> plot(arima1,main="SIMULAZIONE DI UN PROCESSO ARIMA(1,1,1)",col="red")

 

 

 

 

Stima dei parametri ar 1

> ar1fit<-arima(ar1,order=c(1,1,0),include.mean=FALSE)
> ar1fit

Call:
arima(x = ar1, order = c(1, 1, 0), include.mean = FALSE)

Coefficients:
         ar1
      0.6512
s.e.  0.0578

sigma^2 estimated as 0.9409:  log likelihood = -236.31,  aic = 476.63
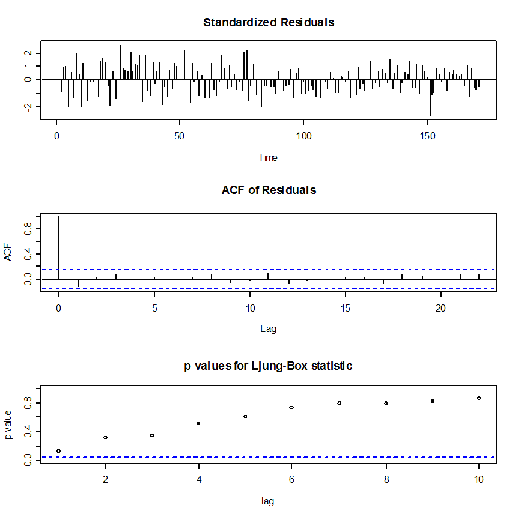
> tsdiag(ar1fit)

Poiché il p- value non è sempre superiore a 0,5 allora il processo non descrive bene i dati reali.

 

Stima dei parametri ar2

> ar22fit<-arima(ar22,order=c(2,1,0),include.mean=FALSE)
> ar22fit

Call:
arima(x = ar22, order = c(2, 1, 0), include.mean = FALSE)

Coefficients:
         ar1      ar2
      0.0527  -0.0252
s.e.  0.0768   0.0767

sigma^2 estimated as 0.1816:  log likelihood = -95.65,  aic = 197.3
> tsdiag(ar22fit)

Anche in questo caso il p- value non è sempre superiore a 0,5 allora il processo non descrive bene i dati reali.

 

Stima dei parametri ma1

> fitma1<-arima(ma1,c(0,1,1))
> fitma1

Call:
arima(x = ma1, order = c(0, 1, 1))

Coefficients:
          ma1
      -0.5363
s.e.   0.0755

sigma^2 estimated as 0.8968:  log likelihood = -232.14,  aic = 468.27
> tsdiag(fitma1)

Anche in questo caso il p- value non è sempre superiore a 0,5 allora il processo non descrive bene i dati reali.

 

Stima dei parametri ARIMA

> arimafit<-arima(arima1, order=c(1,1,1), include.mean=FALSE)
> arimafit

Call:
arima(x = arima1, order = c(1, 1, 1), include.mean = FALSE)

Coefficients:
          ar1     ma1
      -0.0405  0.4255
s.e.   0.2204  0.2044

sigma^2 estimated as 0.9271:  log likelihood = -234.87,  aic = 475.74
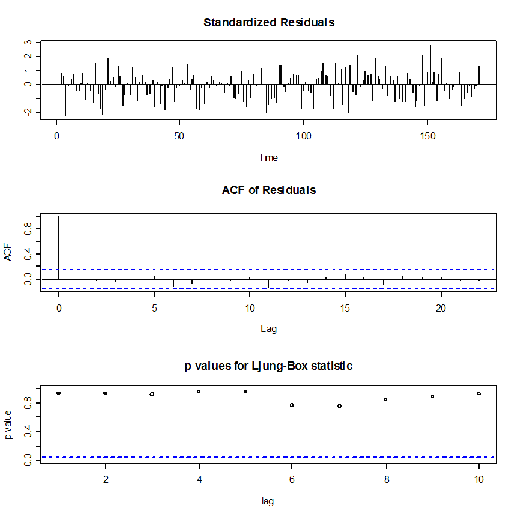
> tsdiag(arimafit)

 

Poiché il p- value si mantiene sempre al di sopra della soglia dello 0,5 allora il modello ARIMA descrive in modo efficiente la nostra serie.

 

 

 

 

 

 

Serie storica di riferimento

L’Italia è tra i primi  Paesi al mondo per importazioni di energia.
Considerando sia i combustibili che l’energia elettrica importata, l’Italia dipende dall’estero per quasi l’84% della propria energia.
Per quanto riguarda l’energia elettrica l’Italia importa una quantità di potenza elettrica media che può andare da un minimo di meno 4000 megawatt (fase notturna, mese di agosto) fino ad un massimo di circa 7500 megawatt (fase diurna, mesi invernali).
Tale importazione avviene da quasi tutti i Paesi confinanti ma soprattutto dalla Francia e dalla Svizzera. Il risultato del mix di fonti italiane è che la corrente elettrica costa il 40% di più che nel resto d’Europa.
Per quel che riguarda invece il petrolio greggio e il gas naturale la maggior parte delle importazioni viene dalla Russia, Libia, Algeria, Iran, paesi dell’ex- URSS, Norvegia, Iraq.
Ciò genera un settore produttivo instabile e risulta essere un forte pericolo per il Paese in quanto un’improvvisa penuria del combustibile o un improvviso aumento dei prezzi potrebbe rendere problematica la produzione di energia elettrica paralizzando il Paese.
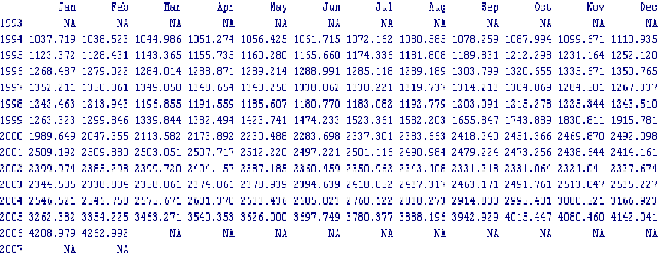
Nell’ambito di tale problematica, nel presente lavoro viene analizzata la serie storica riguardante le importazioni di energia dall’1 gennaio 1993 al  31 febbraio 2007.
La serie storica “Importazioni di energia da Paesi extra UE” è stata scaricata dal sito: http://con.istat.it/amerigo/.

anno  mese       indice

1993 1   1162.968671
1993 2   1021.330243
1993 3   1078.913737
1993 4   1119.51783 
1993 5   1182.052389
1993 6   920.815118 
1993 7   850.68365  
1993 8   1099.967703
1993 9   910.93244  
1993 10  935.406748 
1993 11  1041.726072
1993 12  1061.974077
1994 1   1022.774482
1994 2   939.358833 
1994 3   999.372342 
1994 4   1070.515269
1994 5   999.165539 
1994 6   971.91996  
1994 7   986.80287  
1994 8   1084.349685
1994 9   949.743329 
1994 10  987.200331 
1994 11  1106.707821
1994 12  1246.497267
1995 1   1192.284832
1995 2   1183.073444
1995 3   1182.889013
1995 4   1236.114147
1995 5   1248.28821 
1995 6   1314.302089
1995 7   1181.9969  
1995 8   1061.25776 
1995 9   1041.811726
1995 10  1154.319832
1995 11  1227.323273
1995 12  1323.339291
1996 1   1372.882841
1996 2   1149.251136
1996 3   1312.709111
1996 4   1308.621576
1996 5   1184.149732
1996 6   1133.660423
1996 7   1188.830359
1996 8   1173.607888
1996 9   1284.906438
1996 10  1511.416459
1996 11  1458.869673
1996 12  1630.590019
1997 1   1655.676426
1997 2   1455.653328
1997 3   1307.877527
1997 4   1304.318442
1997 5  1244.681513
1997 6   1242.729451
1997 7   1217.48105 
1997 8   1283.764912
1997 9   1426.51036 
1997 10  1463.20718 
1997 11  1529.710086
1997 12  1604.684087
1998 1   1359.492131
1998 2   1319.131006
1998 3   1123.981951
1998 4   1302.80579 
1998 5   1098.521863
1998 6   1129.450828
1998 7   937.614417 
1998 8   926.750426 
1998 9   1035.490318
1998 10  1031.31804 
1998 11  1022.223182
1998 12  1029.770081
1999 1   1033.724598
1999 2   917.664369 
1999 3   1028.481122
1999 4   1175.479706
1999 5   1155.502215
1999 6   1123.755807
1999 7   1300.532431
1999 8   1459.915593
1999 9   1541.545224
1999 10  1731.210039
1999 11  1714.835374
1999 12  1983.874282
2000 1   2100.011616
2000 2   2272.570819
2000 3   2319.064032
2000 4   2190.237893
2000 5   2333.987728
2000 6   2360.818649
2000 7   2357.63729 
2000 8   2408.676807
2000 9   2767.846166
2000 10  3236.540271
2000 11  3204.378121
2000 12  3146.472765
2001 1   2876.451748
2001 2   2476.395627
2001 3   2573.339839
2001 4   2536.210777
2001 5   2590.376551
2001 6   2485.756273
2001 7   2463.837976
2001 8   2459.580114
2001 9   2326.839704
2001 10  2367.189297
2001 11  2193.808994
2001 12  2270.552226
2002 1   2411.222131
2002 2   2117.204359
2002 3   2101.857382
2002 4   2435.716196
2002 5   2302.793516
2002 6  1959.018417
2002 7   2458.195246
2002 8   2104.338957
2002 9   2114.665121
2002 10  2618.649232
2002 11  2371.247618
2002 12  2592.314568
2003 1   2791.78439 
2003 2   2509.54733 
2003 3   2836.966249
2003 4   2684.247503
2003 5   2111.913814
2003 6   1922.236827
2003 7   2248.331195
2003 8   2274.976726
2003 9   2157.332705
2003 10  2320.494106
2003 11  2191.600872
2003 12  2534.632889
2004 1   2441.344908
2004 2   2268.695784
2004 3   2598.626554
2004 4   2501.849552
2004 5   2557.682054
2004 6   2695.28401 
2004 7   2544.343643
2004 8   2939.806369
2004 9   2750.701902
2004 10  2829.413514
2004 11  3150.802468
2004 12  2925.753745
2005 1   2874.645646
2005 2   2797.722801
2005 3   3232.374402
2005 4   3479.423645
2005 5   3485.907775
2005 6   3401.58866 
2005 7   3812.203832
2005 8   4189.621744
2005 9   4188.143098
2005 10  4172.372815
2005 11  4448.470576
2005 12  4351.659916
2006 1   4921.112961
2006 2   4737.418632
2006 3   4994.843966
2006 4   4525.682015
2006 5   4643.018808
2006 6   4351.41077 
2006 7   4760.985977
2006 8   5239.804513
2006 9   4308.139022
2006 10  4563.657974
2006 11  4454.740172
2006 12  4690.310275
2007 1   4599.203633
2007 2   4224.987999

Funzioni di riferimento

CARICAMENTO PACCHETTO
"library(tseries)"

CARICAMENTO DATI
x<-read.table("C:/Documents and Settings/Giuseppe/Desktop/importazioni di energia extra ue.txt",header=TRUE)
indice<-x\$indice

ANALISI PRELIMINARE
max(indice)
min(indice)
mean(indice)
var(indice)
length(indice)

RICONOSCIMENTO SERIE STORICA
xt<-ts(indice,start=c(1993,1),frequency=12)
is.ts(xt)
xt

ANALISI GRAFICA
plot(xt,ylab="importazioni di enegia",xlab="tempo",main="GRAFICO DELLA SERIE STORICA",lwd=1,lty=1,col="red")
hist(indice,prob=TRUE,col="yellow")

CARICAMENTO PACCHETTO AST
"library(ast)"

STIMA DEL TREND CON IL FILTRAGGIO
xt.filt<-filter(xt,filter=rep(1/25,25))
xt.filt
plot(xt.filt,main="TREND STIMATO CON MEDIA MOBILE",col="green")

SCOMPOSIZIONE MEDIANTE DIFFERENZIAZIONE
xt.diff<-diff.ts(xt)
xt.diff
plot(xt.diff,main="GRAFICO DELLA SERIE STORICA DETRENDIZZATA",col="brown")
xt.diff2<-diff.ts(xt.diff)
plot(xt.diff2,main="GRAFICA DELLA SERIE STORICA DETRENDIZZATA 2",col="brown")

STIMA DEL TREND CON IL LIVELLAMENTO
xt.hw<-HoltWinters(xt,seasonal="additive")
xt.hw
plot(xt.hw)
prev<-predict(xt.hw,n.ahead=5)
prev

DECOMPOSIZIONE DELLA SERIE STORICA CON DEC
dec.fit<-decompose(xt,type="additive")
stag.dec<-dec.fit\$seasonal
trend.dec<-dec.fit\$trend
res.dec<-dec.fit\$random
plot(dec.fit)

DECOMPOSIZIONE DELLA SERIE STORICA CON STL
stl.fit<-stl(xt,s.window="periodic")
attributes(stl.fit)
stag.stl<-stl.fit\$time.series[,1]
trend.stl<-stl.fit\$time.series[,2]
res.stl<-stl.fit\$time.series[,3]
plot(stl.fit,main="GRAFICO DELLA SERIE STORICA DECOMPOSTA- funzione stl")

DECOMPOSIZIONE DELLA SERIE STORICA CON TSR
library(ast)
tsr.fit<-tsr(xt~poly(1)+c)
plot(tsr.fit)
plot(xt.filt)
lines(trend(tsr.fit),col="red")
tsr2.fit<-tsr(xt~loess(1,10)+c)
plot(tsr2.fit)
plot(xt.filt)
lines(trend(tsr2.fit),col="blue")
plot(trend(tsr2.fit),main="COMPARAZIONE DEL TREND STIMATO")
lines(xt.filt,col="red")
lines(trend.stl,col="green")
trend.tsr<-trend(tsr2.fit)
stag.tsr<-seasonal(tsr2.fit)
res.tsr<-residuals(tsr2.fit)

LISCIAMENTO DELLA SERIE STORICA
plot(xt,main="LISCIAMENTO DELLA SERIE STORICA")
lines(smoothts(xt~lo(2,10)),col="red")
lines(smoothts(xt~s(2)),col="blue")
lines(smoothts(xt~p(2)),col="black")

VERIFICA SUL VALORE DELLA MEDIA DEGLI ERRORI
media.residui<-mean(res.stl)
media.residui
n<-length(res.stl)
n
var.residui<-(n/(n-1))*var(res.stl)
var.residui
s<-sqrt(var.residui)
s
test<-(media.residui/(s/sqrt(n)))
test.t
pt(test.t,n-1,lower.tail=F)
qt(0.99,n-1)

VERIFICA DELLA NORMALITA'
stand<-function(x){m=mean(x)
s=(var(x)^0.5)
z=(x-m)/s
return(z)}
res.stand<-stand(res.stl)
res.stand
plot(res.stand,main="DIAGRAMMA DEI RESIDUI STANDARDIZZATI")
abline(h=2.5)
hist(res.stand,main="ISTOGRAMMA DEI RESIDUI STANDARDIZZATI",xlab="Residui",col="green")
plot(density(res.stand,kernel="gaussian"),main="Distribuzione dei residui:lisciamento",col="green")

TEST DI SHAPIRO
shapiro.test(res.stand)

TEST DI AUTOCORRELAZIONE
acf(res.stand,main="Correlogramma dei residui",col="red")

 

PROCESSO STOCASTICO
mean(res.stl)
var(res.stl)
acf(res.stl,type="correlation",plot=TRUE,main="CORRELOGRAMMA DELLA SERIE DEI RESIDUI",col="violet")
acf(res.stl,type="covariance",plot=TRUE,main="GRAFICO DELLE AUTOCOVARIANZE",col="orange")
acf(res.stl,type="correlation",plot=FALSE)
pacf(res.stl,plot=TRUE,main="GRAFICO DELLE CORRELAZIONI PARZIALI",col="green")
pacf(res.stl,plot=FALSE)

 

ALCUNI MODELLI STOCASTICI
1) AR
ar1<-arima.sim(n=170,list(order=c(1,1,0),ar=0.6))
ar1
plot(ar1,main="SIMULAZIONE DI UN PROCESSO AR(1)",col="blue")

ar11<-arima.sim(n=170,list(ar=0.15,sd=sqrt(2.5)))
ar11
plot(ar11,main="SIMULAZIONE DI UN PROCESSO AR(1)",col="brown")
abline(h=2.5)
abline(h=-2.5)

ar2<-arima.sim(n=170,list(order=c(2,1,0),ar=c(0.5,0.4)))
ar2
plot(ar2,main="SIMULAZIONE DI UN PROCESSO AR(2)")

ar22<-arima.sim(n=170,list(ar=0.88,-0.49),sd=sqrt(0.15))
ar22
plot(ar22,main="SIMULAZIONE DI UN PROCESSO AR(2)")
abline(h=0.15)
abline(h=-0.15)

2) MA
ma1<-arima.sim(n=170,list(order=c(0,1,1),ma=-0.7))
ma1
plot(ma1,main="SIMULAZIONE DI UN PROCESSO MA(1)",col="yellow")

ma2<-arima.sim(n=170,list(order=c(0,1,2),ma=c(-0.9,0.3)))
ma2
plot(ma2,main="SIMULAZIONE DI UN PROCESSO MA(2)",col="green")

3) ARIMA
arima1<-arima.sim(n=170,list(order=c(1,1,1),ar=0.05,ma=0.3))
plot(arima1,main="SIMULAZIONE DI UN PROCESSO ARIMA(1,1,1)",col="red")

 

STIMA DEI PARAMETRI
1)
ar1fit<-arima(ar1,order=c(1,1,0),include.mean=FALSE)
ar1fit
tsdiag(ar1fit)

ar22fit<-arima(ar22,order=c(2,1,0),include.mean=FALSE)
ar22fit
tsdiag(ar22fit)

2)
fitma1<-arima(ma1,c(0,1,1))
fitma1
tsdiag(fitma1)

3)
arimafit<-arima(arima1, order=c(1,1,1), include.mean=FALSE)
arimafit
tsdiag(arimafit)

 

Angelo M. Mineo, Una guida all'utilizzo dell'ambiente statistico R, 2003 (in formato PDF)
http://cran.r-project.org/doc/contrib/Mineo-dispensaR.pdf [consultato in data 09/09/’07]
Fabio Frascati, Creare packages per R sotto Windows XP, 2006
http://cran.at.r-project.org/doc/contrib/Fondamenti-0405.pdf [consultato in data 02/09/’07]
Fabio Frascati, Formulario di statistica con R, 2006
http://cran.r-project.org/doc/contrib/Frascati-FormularioR.pdf [consultato in data 05/09/’07]
Maria Maddalena Barbieri, “Appunti di statistica economica”, Università Roma 3
http://host.uniroma3.it/docenti/barbieri/statistica-economica.htm [consultato in data 11/09/’07]
Pagina delle FAQ (Frequently Asked Questions) su R
http://cran.r-project.org/faqs.html [consultato in data 02/09/’07]
Riccardo Lucchetti, “Appunti di analisi delle serie storiche”, Università Politecnica della Marche
http://www.econ.unian.it/lucchetti/didattica/matvario/procstoc.pdf [consultato in data 05/09/’07]
Vito M. R. Muggeo, Giancarlo Ferrara, Il linguaggio R: concetti introduttivi ed esempi, ?? edizione, 2006
http://cran.r-project.org/doc/contrib/nozioniR.pdf [consultato in data 03/09/’07]
Vito Ricci, “R : un ambiente open source per l'analisi statistica dei dati”, Economia e Commercio, (1):69-82,2004
http://www.dsa.unipr.it/soliani/allegato.pdf [consultato in data 10/09/’07]
Walter Zucchini, Oleg Nenadic, “Time Series Analysis with R “,Università di Gottinga
http://www.statoek.wiso.unigoettingen.de/veranstaltungen/zeitreihen/sommer03/ts_r_intro.pdf [consultato in data 08/09/07]
http://sirio.stat.unipd.it/index.php?id=rlink [consultato in data 08/09/07]
http://con.istat.it/amerigo/
http://www.sms.dsems.unile.it/%7Edeiaco/insegna_03.html#materiale