Quando si visitano luoghi turistici, si focalizza sempre l’attenzione sulle bellezze architettoniche e naturali, suscitando una certa emozione. Monumenti, siti archeologici o sculture della natura attirano lo sguardo grazie alla loro bellezza. Anche in Matematica esistono oggetti caratterizzati da una propria attrattiva. Tali oggetti possono essere costituiti da formule o numeri. Il presente articolo mostra proprio alcuni numeri primi, estremamente lunghi, dotati di una bellezza non comune, caratterizzati cioè da una formazione di cifre che da luogo a “sculture matematiche”, dotate di un certo fascino.
Autore: Antonio Bernardo
68. Da Cavalieri alla prima derivata
 Seconda parte della storia dell’analisi infinitesimale. Nella matematica del tardo medioevo per calcolare aree e volumi si applica il metodo di esaustione. Nel 1635 Cavalieri introduce il metodo degli indivisibili che contiene l’idea di segmenti infinitesimi che riempiono una superficie. Qualche anno dopo, Fermat introduce un metodo più algebrico per calcolare massimi e minimi di funzioni, un metodo che fa uso di incrementi ‘infinitesimi’, del rapporto incrementale e, sotto sotto, anche del limite.
Seconda parte della storia dell’analisi infinitesimale. Nella matematica del tardo medioevo per calcolare aree e volumi si applica il metodo di esaustione. Nel 1635 Cavalieri introduce il metodo degli indivisibili che contiene l’idea di segmenti infinitesimi che riempiono una superficie. Qualche anno dopo, Fermat introduce un metodo più algebrico per calcolare massimi e minimi di funzioni, un metodo che fa uso di incrementi ‘infinitesimi’, del rapporto incrementale e, sotto sotto, anche del limite.
69. Le comete Kreutz
 Le comete sono ritenute dei residui fossili della condensazione della nebulosa da cui si è formato il sistema solare. Nell’articolo si parla della famiglia delle comete radenti, delle quali solo in tempi recenti, grazie all’ausilio dei satelliti, si è potuto ipotizzare l’origine comune da una grande cometa progenitrice. L’articolo può tornare utile a chi dovendo fare gli esami di maturità vuole prendere spunto per una tesina. La bigliografia e sitografia finale possono aiutare chi vuole approfondire.
Le comete sono ritenute dei residui fossili della condensazione della nebulosa da cui si è formato il sistema solare. Nell’articolo si parla della famiglia delle comete radenti, delle quali solo in tempi recenti, grazie all’ausilio dei satelliti, si è potuto ipotizzare l’origine comune da una grande cometa progenitrice. L’articolo può tornare utile a chi dovendo fare gli esami di maturità vuole prendere spunto per una tesina. La bigliografia e sitografia finale possono aiutare chi vuole approfondire.
link di approfondimento
ECOLOGICACUP – stanno per scadere le iscrizioni
 Il 31 marzo (2008) scadono le iscrizioni alla gara di ecologia su Internet a squadre "EcoLogicaCup" che, in coppia con Matematicup, realizza un modo di apprendere e insegnare in rete, collaborando tra scuole, università, testate editoriali di prestigio (Repubblica, Kataweb, Le Scienze) enti nazionali e internazionali di ecologia (Oasi WWF, Società Italiana di Ecologia). Iscrivetevi subito.
Il 31 marzo (2008) scadono le iscrizioni alla gara di ecologia su Internet a squadre "EcoLogicaCup" che, in coppia con Matematicup, realizza un modo di apprendere e insegnare in rete, collaborando tra scuole, università, testate editoriali di prestigio (Repubblica, Kataweb, Le Scienze) enti nazionali e internazionali di ecologia (Oasi WWF, Società Italiana di Ecologia). Iscrivetevi subito.
Cosa serve? Dopo che vi sieti iscritti, prendete: un pezzo di spago, cartoncini, pennarelli, spillatrice, carta quadrettata, righello, barattoli, etichette, lente di ingrandimento, macchina fotografica … e correte sul prato. Dopo le esperienze sul campo, tutti davanti al computer a rispondete alle domande. Tanti premi per chi arriva primo!
Riconquistiamo un corretto rapporto tra uomo e natura!
70. Metallica 4, In delegazione dal preside
 Quarto episodio di Metallica, il racconto della scrittrice Anna Cerasoli per padroneggiare i principi del calcolo combinatorio. In questo episodio si parla di una delegazione da mandare dal preside per via di una brutta nota. Ma ce la farà il protagonista a incontrare la sfuggente Metallica?
Quarto episodio di Metallica, il racconto della scrittrice Anna Cerasoli per padroneggiare i principi del calcolo combinatorio. In questo episodio si parla di una delegazione da mandare dal preside per via di una brutta nota. Ma ce la farà il protagonista a incontrare la sfuggente Metallica?
71. Il teorema dei numeri primi
 Da millenni i numeri primi e le loro bizzarre proprietà stuzzicano la curiosità di matematici e appassionati. Tanti teoremi e tante congetture si esprimono con una semplicità disarmante, ma le loro dimostrazioni fanno impazzire da secoli matematici professionisti e dilettanti. Di recente è stato dimostrato l’Ultimo Teorema di Fermat ma solo per capirne la dimostrazione occorrono mesi di studio ai più esperti matematici. Stessa sorte per il Teorema dei Numeri Primi. Resiste invece agli sforzi più accaniti la cosiddetta Ipotesi di Riemann.
Da millenni i numeri primi e le loro bizzarre proprietà stuzzicano la curiosità di matematici e appassionati. Tanti teoremi e tante congetture si esprimono con una semplicità disarmante, ma le loro dimostrazioni fanno impazzire da secoli matematici professionisti e dilettanti. Di recente è stato dimostrato l’Ultimo Teorema di Fermat ma solo per capirne la dimostrazione occorrono mesi di studio ai più esperti matematici. Stessa sorte per il Teorema dei Numeri Primi. Resiste invece agli sforzi più accaniti la cosiddetta Ipotesi di Riemann.
Approfondimenti
72. Intervista a Beppe Scienza
 Manu Monteux ha posto per la nostra rivista alcune domande al noto matematico e giornalista Beppe Scienza sui temi del risparmio gestito. Beppe Scienza, autore di diversi libri di successo e di numerosissimi articoli apparsi sulla stampa italiana, è noto da anni come voce indipendente nel mondo della finanza. Le sue battaglie contro le malefatte compiute dal mondo delle banche sono senza esclusione di colpi. Molte delle cose che dice dovrebbero essere ovvie per chi conosce un minimo di matematica, eppure…
Manu Monteux ha posto per la nostra rivista alcune domande al noto matematico e giornalista Beppe Scienza sui temi del risparmio gestito. Beppe Scienza, autore di diversi libri di successo e di numerosissimi articoli apparsi sulla stampa italiana, è noto da anni come voce indipendente nel mondo della finanza. Le sue battaglie contro le malefatte compiute dal mondo delle banche sono senza esclusione di colpi. Molte delle cose che dice dovrebbero essere ovvie per chi conosce un minimo di matematica, eppure…
Matematicamente.it
Professor Beppe Scienza, lei è noto da anni come voce indipendente nel mondo della finanza e per le sue battaglie contro le malefatte compiute da molti intermediari finanziari: tuttavia molte delle cose che lei dice, per chi ha un minimo di nozioni di matematica, dovrebbero essere ovvie. Per quale motivo invece non è così? Non pensa che ci sia un problema educativo, o quanto meno di scarsità di cultura finanziaria, nel nostro paese?
Beppe Scienza
Non resisto alla tentazione di riportare quanto scritto nel primo capitolo de “Il risparmio tradito”, precisamente a pag. 8: “Per investire è utile fare qualche conto, ma ancora più importante è imparare a filtrare le notizie”. Prendiamo ad esempio i titoli emessi dalle banche (certificati di deposito, obbligazioni ecc.). Da decenni hanno tassi inferiori a quelli dei titoli di Stato (Bot, Btp ecc.). Nei casi più semplici bastano davvero due conti in croce per accorgersi che rendono meno. Perché allora tantissimi risparmiatori li hanno sottoscritti ugualmente? Sicuramente per esempio perché gli impiegati delle banche gli hanno regolarmente raccontato la frottola che sono più sicuri dei titoli del Tesoro; e giornalisti economici gli hanno tenuto bordone, guardandosi bene dal denunciare pubblicamente le falsità raccontategli.
Matematicamente.it
I titoli dei suoi libri di denuncia sono eloquenti: “La pensione tradita”, “Il risparmio tradito”. Ci ricorderebbe cosa è opportuno fare col nostro trattamento di fine rapporto (TFR), visto che l’informazione istituzionale è stata molto lacunosa e, come lei ci ricorda, sono molti gli “avvoltoi”?
Beppe Scienza
In questo caso conviene fare come la larghissima maggioranza dei lavoratori interessati alla riforma del TFR, che ha mangiato la foglia e capito che gli conveniva non credere alle frottole raccontategli dai giornali, dalle radio e dalle televisioni. Si sono infatti tenuti ben stretto il TFR, guardandosi bene dal darlo in pasto all’industria della previdenza integrativa.
Matematicamente.it
E come dovremmo comportarci nei riguardi delle banche? Spesso nelle banche si lavora a budget, per cui al cliente vengono proposti prodotti da un consulente-venditore – più venditore che consulente – che sono remunerativi principalmente per la banca. Ultimamente, per esempio, vanno molto di moda i prodotti appunto della previdenza complementare (polizze vita, fondi pensione ecc.). È ancora valido il suo consiglio di declinare ogni offerta e tenersi i titoli di stato?
Beppe Scienza
Certo, tanto che consiglio di adottare una regola un po’ rozza, ma molto utile: a ogni proposta della banca rispondere di no. La sua osservazione sui budget di vendita è molto giusta e purtroppo la maggior parte dei risparmiatori non si rende ben conto che l’addetto allo sportello è un addetto alle vendite, che tanto più s’ingrazia i suoi superiori quanto più cattivi sono gli investimenti che rifila ai clienti. Di nuovo non è una regola assoluta, ma fondamentalmente è vero che il prodotto peggiore per il cliente è quello migliore per la banca o il promotore finanziario. E vale anche il viceversa: i titoli di Stato, in particolare i Buoni del tesoro indicizzati all’inflazione, vanno bene per i risparmiatori, ma vanno malissimo per la banca o il promotore che ci guadagna pochissimo.
Matematicamente.it
La rata del mutuo è oggi una nota dolente per molti italiani: concorda col consiglio di alcuni consulenti “indipendenti” di scegliere sempre il tasso fisso? Questo consiglio è valido anche in Italia, dove il costo del tasso fisso è molto superiore alla media europea?
Beppe Scienza
Sul basso livello dei cosiddetti consulenti indipendenti potremmo parlare a lungo. Entrando in merito nel problema, di per sé non si può dire se a conti fatti risulterà essere stato più conveniente un mutuo a tasso fisso o variabile. Per anni è stato meno costoso il secondo. È piuttosto un altro l’aspetto da tenere presente per un finanziamento a tasso variabile con piano di rimborso fissato all’inizio, come è di regola. È che la rata di un mutuo a tasso variabile è soggetta al rischio di forti fluttuazioni proprio nei primi anni di vita del mutuo. La cosa è nota a chiunque conosca la materia, ma mi risulta che quasi mai sia stata evidenziata dalle banche e ovviamente neppure dai giornalisti economici, che di regola sono ignoranti come scarpe.
Matematicamente.it
Leggendo i suoi articoli o sfogliando i rapporti di Mediobanca, ci si rende conto che, per quanto riguarda l’investimento azionario, è meglio il “fai da te”. Infatti la quota di fondi di investimento che fa meglio del mercato è statisticamente poco significativa, mentre i fondi che fanno peggio sono la maggioranza. Il classico della letteratura finanziaria “A Random Walk Down Wall Street”, di Burton Malkiel del 1973, è tuttora attuale? Lo consiglierebbe ancora ai risparmiatori, oltre che, malignamente, ai gestori?
Beppe Scienza
In realtà il risparmio gestito fa quasi sempre peggio di chi investe da solo anche nel reddito fisso, non solo nelle azioni. E se è vero, come è vero, che fa peggio delle medie di mercato, allora ne discende che fa mediamente peggio anche di uno che sparpagli il suo investimento su un ampio numero di titoli scelti a caso (questa è la tesi, dimostrata, di Malkiel). Questo però i gestori lo sanno benissimo. Se razzolano male spesso non è per incompetenza, ma perché i loro obiettivi divergono da quelli dei loro clienti. Non puntano a farli guadagnare, ma a produrre utili per la società che li stipendia; o per il gruppo a cui essa appartiene.
Matematicamente.it
Ci può indicare qualche regola che a suo giudizio deve adottare chi vuole a tutti i costi investire nel mercato azionario?
Beppe Scienza
Quella più semplice è servirsi degli ETF (Exchange Traded Fund) che sono titoli che replicano fedelmente e con costi bassi determinati mercati azionari.
Matematicamente.it
Per finire, è d’accordo con la citazione in capo alla voce “finanza” su Wikipedia: « Finanza: l’arte o scienza di gestire redditi e risorse per il massimo beneficio del gestore » (Ambrose Bierce, “Il dizionario del diavolo”)?
Beppe Scienza
Carina, non la conoscevo. La riporterò in un mio prossimo libro.
Scarica il pdf del Magazine
Per conoscere Beppe Scienza
Somma degli angoli interni e somma degli angoli esterni di un quadrilatero: VIDEO
In questo video si verifica con l’uso del software open-source Geogebra che la somma degli angoli interni e la somma degli angoli esterni di un quadrilatero misura 360°. {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_somma_angoli.flv{/flvremote}
73. I risultati di PISA 2006, aspettative e miti
 Lo scorso dicembre hanno suscitato grande clamore i dati relativi all’indagine OCSE PISA 2006. Dai risultati di questa ricerca sulle competenze di scienze, matematica e lettura degli studenti quindicenni, sono emerse notizie poco confortanti per l’Italia: i nostri ragazzi si sono classificati al 39o posto sui 57 paesi che hanno aderito all’indagine, praticamente in fondo alla classifica.
Lo scorso dicembre hanno suscitato grande clamore i dati relativi all’indagine OCSE PISA 2006. Dai risultati di questa ricerca sulle competenze di scienze, matematica e lettura degli studenti quindicenni, sono emerse notizie poco confortanti per l’Italia: i nostri ragazzi si sono classificati al 39o posto sui 57 paesi che hanno aderito all’indagine, praticamente in fondo alla classifica.
.
Parole chiave: indagine OCSE PISA 2006, PISA giovani, indagine giovani, metodologia indagine, risultati indagine PISA, PISA scuola
Approfondimenti
AA. VV. Valutare le competenze in scienze, lettura e matematica, quadro di riferimento di PISA 2006, Armando Editore 2007
http://www.invalsi.it/ric-int/Pisa2006/sito/docs/Quadro_riferimento_PISA2006.pdf
AA.VV, Risultati di PISA 2006, un primo sguardo d’insieme, a cura di INVALSI, dicembre 2007.
http://www.invalsi.it/download/pdf/pisa06_Primirisultati_PISA2006.pdf
Complete executive summary
http://www.oecd.org/dataoecd/15/13/39725224.pdf
Il sito dell’INVALSI relativo a PISA 2006
http://www.invalsi.it/invalsi/ri/pisa2006.php?page=pisa2006_it_00
Il sito dell’OCSE relativo a PISA 2006
http://www.oecd.org/pages/0,3417,en_32252351_32236191_1_1_1_1_1,00.html
Didattica della matematica secondo l’UMI
http://umi.dm.unibo.it/italiano/Didattica/didattica.html
Mathesis, Società italiana di scienze matematiche e fisiche
http://www.mathesisnazionale.it/PagineHTML/index.htm
M. G. Ottavini, S. Magnani, R. Ricci, Metodi statistici per la valutazione di abilità e competenze
http://www.matematica.it/paola/Siena_UMI05.pdf
74. Geogebra per operare dinamicamente con la matematica
 Geogebra è un software libero che permette di operare in modo interattivo con la matematica. Con esso è possibile disegnare punti, segmenti, rette, coniche, funzioni e soprattutto è possibile modificarle dinamicamente. Contemporaneamente in una apposita finestra di algebra vengono visualizzate le coordinate dei punti e le misure di segmenti, angoli, perimetri, aree. La finestra dei numeri e quella delle figure interagiscono dinamicamente tra di loro. Si presentano alcune attività didattiche che si possono svolgere nella secondaria di primo grado.
Geogebra è un software libero che permette di operare in modo interattivo con la matematica. Con esso è possibile disegnare punti, segmenti, rette, coniche, funzioni e soprattutto è possibile modificarle dinamicamente. Contemporaneamente in una apposita finestra di algebra vengono visualizzate le coordinate dei punti e le misure di segmenti, angoli, perimetri, aree. La finestra dei numeri e quella delle figure interagiscono dinamicamente tra di loro. Si presentano alcune attività didattiche che si possono svolgere nella secondaria di primo grado.
Parole chiave: geogebra, didattica della matematica, geometria, secondaria primo grado
Approfondimenti
http://www.math.fau.edu/~mhohen/
http://www.geogebra.org/forum/
http://home.windstream.net/joelkahn/
75. Recen…siti
 Due siti di matematica ricchi di contenuti dinamici e innovativi sulla matematica da vedere, da ascoltare e da manipolare.
Due siti di matematica ricchi di contenuti dinamici e innovativi sulla matematica da vedere, da ascoltare e da manipolare.
http://mathsite.math.berkeley.edu/intro.html
http://www.matematita.it/materiale/index.php
consulta la sezione dei siti di matematica
I. Stewart, Com’è bella la matematica
Ian Stewart, Com’è bella la matematica. Lettere a una giovane amica, Bollati Boringheri, 2006
 Se il grande matematico inglese Hardy esordiva nel suo libro del 1940, Apologia di un matematico, affermando che "Per un matematico di professione è un’esperienza melanconica mettersi a scrivere di matematica", Ian Stewart, è convinto del contrario. I tempi sono cambiati, scrive Stewart nell’introduzione del suo libro "Una giornata tipo del grande studioso di Cambridge [Hardy] consisteva in quattro ore al massimo di riflessione intensa sui problemi della ricerca mentre il resto del tempo trascorreva fra le partite a cricket e la lettura dei giornali. Rimaneva probabilmente lo spazio per qualche sporadico incontro con gli studenti. Oggi la giornata tipo di un accademico è lunga dieci o dodici ore, divise fra l’insegnamento, le richieste di sovvenzioni, la ricerca da proseguire, e ampie dosi d’inutile burocrazia necessarie ad avviare qualsiasi progetto creativo."
Se il grande matematico inglese Hardy esordiva nel suo libro del 1940, Apologia di un matematico, affermando che "Per un matematico di professione è un’esperienza melanconica mettersi a scrivere di matematica", Ian Stewart, è convinto del contrario. I tempi sono cambiati, scrive Stewart nell’introduzione del suo libro "Una giornata tipo del grande studioso di Cambridge [Hardy] consisteva in quattro ore al massimo di riflessione intensa sui problemi della ricerca mentre il resto del tempo trascorreva fra le partite a cricket e la lettura dei giornali. Rimaneva probabilmente lo spazio per qualche sporadico incontro con gli studenti. Oggi la giornata tipo di un accademico è lunga dieci o dodici ore, divise fra l’insegnamento, le richieste di sovvenzioni, la ricerca da proseguire, e ampie dosi d’inutile burocrazia necessarie ad avviare qualsiasi progetto creativo."
Com’è bella la matematica è il tentativo di Ian Stewart, noto matematico inglese e prolifico divulgatore, di ‘aggiornare’ il libro di Hardy. La finzione narrativa si basa su una serie di lettere scritte da Stewart a Meg, una studentessa di scuole superiori appassionata di matematica, che nel corso del tempo trascorso tra una lettera e l’altra si iscrive a Matematica, fa il dottorato e infine conquista un incarico universitario.
Le lettere rispondono a una serie di domande che Meg, personaggio probabilmente inventato, pone a Stewart. Perché fare matematica? I matematici, risponde Stewart, li incontriamo ogni giorno e in ogni luogo, eppure non ci viene mai in mente che il nostro direttore di banca possa essere laureato in matematica. I produttori di DVD, di lettori MP3, di film di animazione utilizzano una schiera di matematici. Gli effetti speciali nei film e tutti i moderni film di animazione che si basano sulla grafica computerizzata usano in maniera massiccia la matematica. La grafica computerizzata non è semplicemente il risultato dell’uso stupido dei computer: occorre la geometria tridimensionale, la matematica della diffusione luminosa, l’interpolazione tra un fotogramma e l’altro per rendere fluida l’immagine. Il film Toy Story, per esempio, ha portato ad almeno una ventina di pubblicazioni matematiche.
Prima di iscriversi al corso di laurea in matematica, Meg chiede al noto accademico qual è la matematica e che cosa si insegna nei corsi più avanzati. A scuola, scrive Stewart, tu leggi Shakespeare, Dickens, Eliot e supponi che non esistano livelli più alti della letteratura. Per analogia ti domandi se la matematica che impari a scuola corrisponde alla matematica di livello superiore. La matematica che insegnano a scuola è "un insieme di piccoli trucchi del mestiere" che si applicano in contesti molto semplici. E’ come per un apprendista falegname che impara a mettere chiodi ma non vede come si fabbrica una sedia o un mobile. Mentre nella scuola superiore una parte cospicua di quella che viene chiamata matematica è in realtà aritmetica ed ha a che fare con i numeri, all’università si impara ad astrarre dai numeri, a generalizzare, a formalizzare con teorie astratte come quella dei gruppi.
Di fronte a questa grande varietà di studi matematici la domanda è allora quella di capire che cos’è la matematica e di darne una definizione. "Le definizioni, scrive Stewart, sono paralizzanti, sbarrano la strada alla creatività e alla diversità. Una definizione cerca implicitamente di ridurre le possibili varianti di un concetto a un’unica soluzione. La matematica, come qualsiasi campo in via di sviluppo, è sempre fonte di stupore." La definizione di matematica preferita da Stewart è quella di Lynn Arthur Steen secondo la quale la matematica è "la scienza della forma significante".
Un altro tema è la filosofa della matematica, tradizionalmente divisa tra platonismo e formalismo. In che senso, per esempio, esiste un cerchio matematico? Per i platonisti il cerchio matematico è un’idea non realizzata in questo mondo e che esiste indipendentemente dalla mente umana. I formalisti giudicano queste osservazioni insensate e confuse. Un’affermazione del tipo 2+2=4 per un formalista è un gioco senza significato basato su rigide regole esplicite. Il formalismo di fatto morì quando Goedel dimostrò che nessuna teoria puramente formale è in grado di esprimere interamente l’aritmetica. Resteranno sempre ‘fuori dal gioco’ degli enunciati matematici che non sono né dimostrabili né indimostrabili. Più recentemente, Reuben Hersh ha sostenuto che la matematica è un’attività umana che si svolge all’interno di una società e che si sviluppa storicamente. Si tratta di una descrizione moderna di quella che è l’attività dei matematici che non tocca e non specifica il contenuto di questa attività. Così posta mancherebbe di un anello importante che ha a che fare con una sorta di coerenza logica interna dell’attività. Se, per esempio, tutti i matematici si accordassero all’unanimità che $pi$ vale 3, ciò non sarebbe vero e non avrebbe senso per la comunità dei matematici. "La matematica, pur essendo un prodotto della mente umana, non si piega alla volontà umana." Quando due matematici discutono prima o poi uno si ferma e dice "mi dispiace, hai ragione tu, ora ho capito dove sbagliavo". Per capire meglio il punto di vista di Hersh si può seguire il suo stesso esempio relativo al denaro. Il mondo gira intorno al denaro ma cos’è il denaro? dei pezzi di carta? dei dischetti di metallo? Non sono neppure dei numeri in un calcolatore. Infatti, se il computer della banca si rompe i soldi sono sempre tuoi. Anche il denaro è un costrutto socialmente condiviso ma con delle restrizioni. Se vai in banca e dici al direttore che i tuoi soldi dovrebbero essere di più di quelli che risultano sul conto, il direttore non ti risponderà "nessun problema, eccole altri dieci milioni, buona giornata". La matematica, come in fondo il denaro, pur essendo un costrutto socialmente condiviso ha una certa inevitabilità logica e tutte le menti devono pervenire alla stessa matematica.
Ma la matematica è universale? Gli extraterrestri conterebbero come noi? Stewart ritiene che la matematica sia strettamente connessa alla nostra fisiologia alle nostre esperienze e alle nostre caratteristiche psicologiche. Punti e linee, per esempio, sembrano le basi naturali per una teoria della forma ma sono anche gli elementi fondamentali in cui il nostro sistema visivo scompone il mondo. Gli elementi fondamentali di un sistema visivo alieno potrebbero essere invece luci e ombre, o movimento e immobilità, la frequenza delle vibrazioni. La stessa osservazione si può fare per i numeri discreti (1, 2, 3, …); ci sembrano universali perché nascono dalla nostra tendenza ad assemblare oggetti simili: probabilmente l’aritmetica è nata a causa dell’avvicendarsi delle stagioni e per il commercio, legato alla proprietà di beni. Creature extraterrestri fluttuanti che vivono, per esempio, su pianeti come Giove potrebbero non avere alcuna idea di proprietà individuale: prima di arrivare fino a contare tre oggetti, gli oggetti stessi si sarebbero dissolti nel vento di ammoniaca. Potrebbero invece essere molto esperti nella dinamica dei flussi turbolenti.
Come si studia la matematica? Molti studenti sono convinti che quando ci si blocca su qualche argomento la cosa migliore sia fermarsi, tornare indietro e rileggere la parte incriminata finché non si intravede la luce. Questo metodo è quasi sempre fatale. Per Stewart, la prima regola è proseguire. Occorre segnarsi il punto in cui ci si è fermati, spesso la frase successiva o il paragrafo successivo chiariranno la difficoltà. Se così non fosse, occorre ritornare dove ci si era bloccati e ripercorrere i passi fino a raggiungere un punto dove si è sicuri di aver capito tutto e si riprende da lì. Nell’ultima parte del libro, Stewart, con un po’ di ironia descrive la struttura della ‘tribù dei matematici mondiali’: un giovane ricercatore parte dalla posizione di SSDX (studente specializzando del dottor X), per diventare PGR (promettente giovane ricercatore), subito dopo un RC (ricercatore confermato) e poi SS (scienziato senior), GV (grande vecchio) e GE (guru emerito).
La lettura di questo libro mi è sembrata particolarmente interessante, a mio giudizio è uno dei pochi libri di tipo ‘divulgativo’ ben fatto. Qualche sbavatura non manca, l’editore ha lasciato più di una decina di refusi sparsi per il libro e per un editore come Bollati Boringheri mi sembra un eccessivo disinteresse per libri i di matematica che pure hanno firme autorevoli. L’autore ha invece trascurato in qualche passaggio la finzione base del suo libro: se scrive delle lettere a una che dopo tanta fatica è diventata docente universitaria di matematica non credo sia ipotizzabile che debba spiegargli come si giustifica il fatto che "meno per meno fa più". Se voleva discutere questo tema probabilmente doveva presentarlo all’inizio del libro quando Meg è ancora una studentessa di Liceo. Si tratta comunque di piccoli ‘difetti’ che si notano proprio perché il libro si presenta particolarmente ben fatto. Complessivamente poi non è ben chiaro se la matematica sia bella perché la incontriamo dappertutto come applicazione alla vita di tutti i giorni e come lettura del mondo o se come ci si aspettava leggendo il titolo del libro abbia un valore estetico e accattivante per la mente umana.
M. F. Atiyah, Siamo tutti matematici
Michael F. Atiyah, Siamo tutti matematici, Di Renzo Editore, 2007
 Su qualunque argomento, non c’è parola più attendibile di quella di un addetto ai lavori; meglio ancora se si tratta dell’opinione di un esperto del settore. Quale miglior modo, dunque, di osservare la matematica che farlo dal punto di vista di un suo autorevole esponente?
Su qualunque argomento, non c’è parola più attendibile di quella di un addetto ai lavori; meglio ancora se si tratta dell’opinione di un esperto del settore. Quale miglior modo, dunque, di osservare la matematica che farlo dal punto di vista di un suo autorevole esponente?
Nel contesto matematico, sicuramente Michael Francis Atiyah riveste un ruolo di spicco a livello mondiale, come dimostrano i numerosi riconoscimenti ottenuti nel corso della sua lunga attività, tra l’altro non ancora conclusa, dato che egli è attualmente professore presso l’Università di Edimburgo. La sua breve opera dal titolo “Siamo tutti matematici”, che rientra a tutti gli effetti nel genere letterario del saggio, può essere considerata come una chiacchierata dell’autore riguardo a vari temi inerenti la matematica. Il tono del discorso è molto colloquiale e numerosi sono i riferimenti alla vita dell’autore stesso, il quale parla in prima persona.
Nella prima parte del libro si parla del rapporto tra la matematica e la mente umana, un tema di cui si è sempre molto discusso e che è alla base della natura stessa della disciplina. A tal proposito, ecco un breve ma significativo frammento di testo: Sappiamo che il cervello umano è diviso in due parti – l’emisfero sinistro e quello destro – che hanno ruoli fondamentalmente diversi: un emisfero sovrintende alle funzioni del linguaggio, mentre l’altro agli aspetti spaziali. Dove si colloca, allora, la matematica? Quale parte del cervello entra in gioco nel ragionamento di tipo logico-numerico? La mia personale opinione è che la geometria sia legata alla visione e l’algebra al linguaggio”. In questo estratto, così come in tutto il libro, l’autore non si limita a riportare semplicemente i fatti, ma espone anche la propria opinione a riguardo.
Un importante rilievo viene dato, in varie parti del testo, al rapporto tra matematica e fisica, tema molto caro ad Atiyah. Il suo nome è ben conosciuto nel mondo dei fisici, ai quali ha aperto diverse porte grazie ai propri lavori: nel corso degli anni, infatti, sono state trovate fondamentali applicazioni delle teorie matematiche di Atiyah nel campo della fisica. Tra i principali risultati che ha conseguito nell’ambito della ricerca, l’autore parla in particolare del forte impulso dato alla K-teoria e del fondamentale “teorema dell’indice”; quest’ultimo, va ricordato, gli valse la medaglia Fields nel 1966.
Un ampio spazio è dedicato all’evoluzione della matematica nel XX secolo. Si tratta di una panoramica sulle branche della matematica che maggiormente hanno attirato su di sé la propria attenzione nel corso del ‘900, in particolare vengono segnalati i risultati più significativi raggiunti e i personaggi che hanno contribuito a delineare la storia della matematica novecentesca. Il XX secolo, tuttavia, non viene considerato come una monade temporale: interessanti sono anche i numerosi paragoni con il passato, così come di straordinario interesse sono le previsioni di chi scrive riguardo alle direzioni che prenderà la matematica nel secolo appena iniziato. Vale a la pena di soffermarsi a leggere quanto riportato in merito: Quella del XXI, come sarà? Ho già detto che prevedo che il nostro secolo vedrà una grande influenza della matematica quantistica o, se preferite, della matematica a infinite dimensioni. La matematica quantistica potrebbe, in un futuro, contribuire a comprendere correttamente l’analisi, la geometria, la topologia e l’algebra di diversi spazi di funzioni non lineari. Ma è meglio fermarsi qua, per non rovinare la sorpresa ai futuri lettori. La parte finale del libro contiene delle personali riflessioni sulle enormi responsabilità della scienza nella società contemporanea, dove spesso e volentieri si è fatto un uso improprio di importanti risultati scientifici. Atiyah espone la propria opinione senza mezzi termini, indicando con chiarezza la propria linea di pensiero su temi molto delicati, come la moralità dell’uso della bomba atomica, l’organizzazione Pugwash, la questione cinese, i test nucleari condotti da India e Pakistan.
Quella fatta finora è solo una sommaria descrizione dei rami principali in cui si snoda l’intera opera. Sarebbe davvero arduo citare tutte le tematiche affrontate. D’altronde, non si tratta di un testo didattico, né tantomeno divulgativo, per cui risulta difficile suddividerlo in blocchi ben separati e distinti tra loro. Leggere “Siamo tutti matematici” equivale ad osservare la matematica, e la scienza in genere, con gli occhi di qualcun altro; non dovrebbe, tuttavia, essere una visione molto distorta, dato che questo qualcuno è un matematico di rilievo come Michael Atiyah
Amir D. Aczel, Il taccuino segreto di Cartesio
Amir D. Aczel, Il Taccuino Segreto di Cartesio
Storia di un genio del Seicento e della misteriosa formula matematica che non volle rivelare
Mondatori, 2006, pp. 250.
 A mezzanotte Amir Aczel vagava smarrito in una tempesta di neve da qualche parte nell’Ontario; uscito dall’autostrada per cercare un posto dove aspettare che la tempesta finisse, giunse … alla conclusione che si era perso. A salvarlo fu la tecnologia del GPS che gli permise di localizzare la sua posizione e farsi guidare da un operatore al telefono (siamo nel 2002 e i sistemi di navigazione tramite GPS non erano così avanzati come sono oggi). Questo ‘salvataggio’ così provvidenziale lo fece riflettere su quanto fosse importante l’invenzione di Cartesio: la tecnologia che è alla base del GPS funziona infatti grazie all’invenzione del sistema di coordinate cartesiane.
A mezzanotte Amir Aczel vagava smarrito in una tempesta di neve da qualche parte nell’Ontario; uscito dall’autostrada per cercare un posto dove aspettare che la tempesta finisse, giunse … alla conclusione che si era perso. A salvarlo fu la tecnologia del GPS che gli permise di localizzare la sua posizione e farsi guidare da un operatore al telefono (siamo nel 2002 e i sistemi di navigazione tramite GPS non erano così avanzati come sono oggi). Questo ‘salvataggio’ così provvidenziale lo fece riflettere su quanto fosse importante l’invenzione di Cartesio: la tecnologia che è alla base del GPS funziona infatti grazie all’invenzione del sistema di coordinate cartesiane.
A ben guardare il numero di applicazione del sistema di coordinate cartesiane nella nostra vita quotidiana è impressionante: tutto ciò che facciamo o vediamo o usiamo nella vita di ogni giorno ha qualcosa a che fare con la grande invenzione di Cartesio. Da qui l’idea dell’autore di dedicare un libro alla biografia di questo personaggio che ha segnato una svolta nel mostro modo di vivere e di pensare.
Aczel si reca a Parigi sulle orme di Cartesio, lì ha modo di consultare lettere originali di Cartesio a Mersenne, edizioni originali delle opere di Cartesio e a un certo punto scopre che Cartesio aveva tenuto un taccuino segreto di cui si erano perse le tracce.
Il libro di Aczel, nonostante il tono un po’ da romanzo poliziesco, e il vago tentativo di imitare romanzi di successo, è sostanzialmente una biografia di Cartesio, ricca di informazioni e di commenti delle sue opere. Non è un saggio per specialisti; è scritto principalmente per chi vuole capire il ruolo di Cartesio nel mondo moderno.
Sullo sfondo del racconto la storia di un libro e di alcune ricerche matematiche che Cartesio sembra abbia scritto e che sono andati perduti. Le vicende di questa ‘formula’ misteriosa si intersecano poi con la storia dei Rosacroce, una confraternita segreta alla quale non è ben chiaro se Cartesio abbia mai aderito. Alla fine del libro Aczel rivela questa misteriosa formula.
Bruno D’Amore, Matematica dappertutto
Bruno D’Amore, Matematica dappertutto. Percorsi matematici inusuali e curiosi, Pitagora Editrice, Bologna, 2007, pp.88
 Bruno D’Amore ci mostra una matematica che ha invaso tutte le altre forme della cultura umana in 14 brevi ma intensi percorsi, ben illustrati e ricchi di citazioni. Per citarne qualcuno: la superformula di Lamé-Gielis
Bruno D’Amore ci mostra una matematica che ha invaso tutte le altre forme della cultura umana in 14 brevi ma intensi percorsi, ben illustrati e ricchi di citazioni. Per citarne qualcuno: la superformula di Lamé-Gielis
$frac 1
ho =
oot{n_1} {|frac{1}{a}cos(frac m 4 phi)|^{n_2}+|frac 1 b sin(frac m 4 phi)|^{n_3}}$
che con opportuni valori dei parametri a, b, m, n1, n2, n3, permette di ottenere una grande quantità di forme geometriche che effettivamente si incontrano in natura, dai cristalli alle conchiglie, dalle alghe alle foglie. D’amore ci mostra il confronto tra le forme geometriche disegnate per mezzo della formula e le foto degli oggetti reali.
Divertente anche il capitolo in cui confronta l’ignoranza matematica di alcuni scienziati con le competenze raffinate di alcuni scrittori. Gilbert White (1720-1793) studioso di uccelli, dallo studio di un esemplare di cavaliere, un uccello di palude, dal peso di 120 g e lunghezza delle zampe 20,4 cm, trovò che il rapporto peso/lunghezza delle zampe doveva essere 120:20,4 = 5,8. Quando lo stesso White catturò un fenicottero, simile al cavaliere ma molto più pesante, 1,82 kg su zampe lunghe 50 cm, osservò che la proporzione non era la stessa di quella del cavaliere, il fenicottero avrebbe dovuto infatti avere le zampe di 3m. Da qui White dedusse che la natura non lavora con ‘armonia matematica’. Jonathan Swift (1667-1745) nel suo famoso romanzo I Viaggi di Gulliver scrive che quando Gulliver raggiunge il paese di Lilliput, i matematici di questo paese avendo scoperto che la statura di Gulliver eccedeva la loro nella proporzione di dodici a uno, e considerando che i loro corpi erano simili al suo, dedussero che doveva contenere 1728 corpi loro e che quindi Gullier aveva bisogno di tanto cibo quanto ne occorreva per altrettanti lillipuziani. Come mai un naturalista come White non se è reso conto che il peso degli uccelli, va pensato come un volume e quindi va rapportato con il cubo delle lunghezze (quella delle gambe) mentre Swift lo aveva capito? Scrivendo infatti correttamente la proporzione si osserva che la natura lavora armonicamente anche negli uccelli: $120:20,43=1820:503$.
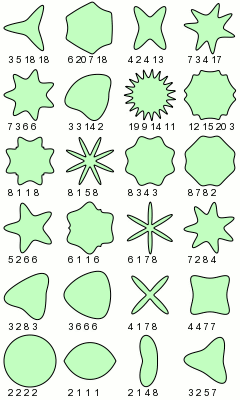
Alcune immagini della superformula per i valori dei parametri indicati. Immagine da http://it.wikipedia.org/wiki/Superformula
76. Lo scaffale dei libri
 Recensioni di: Beppe Scienza, Il risparmio tradito, come difendersi da bancari, assicuratori… e giornalisti, prefazione di Beppe Grillo – Brian Greene, L’universo elegante – Superstringhe, dimensioni nascoste e la ricerca della teoria ultima – AA. VV., La matematica nel mondo della natura, a cura di L. Capocaccia Orsini e L. Pusillo – AA. VV., Tutti i numeri sono uguali a cinque, a cura di S. Sandrelli, D. Gouthier, R. Ghattas – Enrico Giusti,Piccola storia del calcolo infinitesimale dall’antichità al Novecento – Tamás Varga, Fondamenti di logica per insegnanti – AA. VV., Vite matematiche. Protagonisti del ‘900 da Hilbert a Wiles, a cura di C. Bartocci, R. Betti, A. Guerraggio, R. Lucchetti
Recensioni di: Beppe Scienza, Il risparmio tradito, come difendersi da bancari, assicuratori… e giornalisti, prefazione di Beppe Grillo – Brian Greene, L’universo elegante – Superstringhe, dimensioni nascoste e la ricerca della teoria ultima – AA. VV., La matematica nel mondo della natura, a cura di L. Capocaccia Orsini e L. Pusillo – AA. VV., Tutti i numeri sono uguali a cinque, a cura di S. Sandrelli, D. Gouthier, R. Ghattas – Enrico Giusti,Piccola storia del calcolo infinitesimale dall’antichità al Novecento – Tamás Varga, Fondamenti di logica per insegnanti – AA. VV., Vite matematiche. Protagonisti del ‘900 da Hilbert a Wiles, a cura di C. Bartocci, R. Betti, A. Guerraggio, R. Lucchetti
Parole chiave: libri di matematica, divulgazione matematica, biografie matematici, economia, risparmio tradito, superstringhe, matematica e natura, storia dell’analisi, logica per insegnanti
Link indicati
Tutti i numeri sono uguali a cinque
Fondamenti di logica per insegnanti Capitolo primo
Roberto Lucchetti, Passioni per Trilli
Roberto Lucchetti, Passione per Trilli. Alcune idee dalla matematica, Springer, 2007, pp.154
 Trilli è la fatina innamorata di Peter Pan. Cosa c’entri con la matematica lo si scopre soltanto a pagina 123 del libro: "la matematica è un mondo vivo, che contiene anche tante contraddizioni, pieno di difetti. La matematica è possessiva, gelosa e incline alla vanità: proprio come Trilli."
Trilli è la fatina innamorata di Peter Pan. Cosa c’entri con la matematica lo si scopre soltanto a pagina 123 del libro: "la matematica è un mondo vivo, che contiene anche tante contraddizioni, pieno di difetti. La matematica è possessiva, gelosa e incline alla vanità: proprio come Trilli."
Lucchetti ha voluto scrivere un libro di matematica e sulla matematica presentandocela sotto l’aspetto di disciplina brillante e variegata, una disciplina che incontri anche dove non te lo aspetti.
Professore di Analisi presso il Politecnico di Milano, appassionato studioso di Teoria dei Giochi, autore di un libro divulgativo di successo su questa teoria (Di duelli, scacchi e dilemmi, Mondatori, 2001), Lucchetti presenta in sei capitoli, altrettanti temi di matematica, descrivendone le idee in modo non tecnico, convinto che le idee importanti della matematica si possano comunicare senza formule e senza usare il linguaggio tecnico di questa disciplina, linguaggio incomprensibile alla maggior parte dei lettori comuni.
Fanno da Intermezzo a queste storie di matematica altrettante storie ‘personali’ e semiserie dell’autore: una poesia, un commento all’ultimo mondiale di calcio e altre amenità che in un libro di matematica disorientano il lettore ma lo coinvolgono sul piano più strettamente personale.
Ma veniamo ai contenuti matematici, si tratta per lo più di temi che hanno attinenza con la teoria dei giochi: dai primi elementi di questa teoria alle sue applicazioni alle scienze sociali: il teorema di Arrow sulle difficoltà a prendere decisioni ‘democratiche’ in un gruppo di persone e l’indice di Shapley che misura la ‘forza’ dei singoli componenti di un gruppo cooperativo.
Oltre ai temi di teoria dei giochi Lucchetti discute anche delle problematiche dell’infinito in matematica, il passaggio dalle strutture numeriche alla strutture algebriche, qualche biografia controversa di matematici del ‘900, in particolare Nash e von Neumann, principali artefici della teoria dei giochi.
Un libro per tutti: adulti e ragazzi, docenti e studenti, professionisti e semplici appassionati di Trilli.
R. Clerico e P. Fabbri, Rudi simmetrie
Rodolfo Clerico e Piero Fabbri, Rudi simmetrie, CS libri, 2007, pp. 127
 Rudi Mathematici, rivista on line di matematica, nata nel lontano 1999, è diventata un libro di carta, o meglio ha prodotto un libro che si può leggere anche senza stare davanti al computer. Gli autori finora sempre celati da misteriosi nick si sono dovuti rivelare con i loro nomi veri; la carta stampata non ammette tanti misteri. E così scopriamo che dietro la divertente rivista pdf ci sono tre persone in carne e ossa; lascio a voi la possibilità di scoprire chi sono e cosa fanno.
Rudi Mathematici, rivista on line di matematica, nata nel lontano 1999, è diventata un libro di carta, o meglio ha prodotto un libro che si può leggere anche senza stare davanti al computer. Gli autori finora sempre celati da misteriosi nick si sono dovuti rivelare con i loro nomi veri; la carta stampata non ammette tanti misteri. E così scopriamo che dietro la divertente rivista pdf ci sono tre persone in carne e ossa; lascio a voi la possibilità di scoprire chi sono e cosa fanno.
Nel libro sono presentati sostanzialmente sette temi di divulgazione della matematica o forse è meglio dire sette tematiche strettamente connesse alla matematica. Come mia abitudine vi racconto brevemente cosa il lettore può trovare nel libro.
Il primo dei temi proposti introduce alla problematica del raccontare la storia della matematica, la storia della ricerca e dei ricercatori. Un aneddoto su tutti: Julia Robinson, ricercatrice non da poco, visto che ha poi risolto il X problema di Hilbert, per essere assunta come ricercatrice di matematica è costretta a redigere un rapporto del suo lavoro, rapporto che è diventato famoso e significativo: "Lunedì: Provato a dimostrare teorema; Martedì: Provato a dimostrare teorema; Mercoledì: provato a dimostrare teorema; Giovedì: provato a dimostrare teorema; Venerdì: Teorema falso."
La narrazione preferita dagli autori del libro non è sempre quella lineare di una storia che si lascia raccontare dall’inizio alla fine. Clerico e Fabbri preferiscono percorsi più tortuosi e originali. A che punto è la notte è un pezzo che ha tanti inizi ma parla tante volte della stessa cosa: la teoria dei gruppi.
In Difficile contare fino a dieci, gli autori partono da un giro sul cavalluccio di una giostra per parlare di astronomia, delle discussioni recenti su quali debbano essere i pianeti del sistema solare, per poi arrivare alle discussione sulla geometria dello spazio.
Altri capitoli del libro sono dedicati alle trasformazioni geometriche, tassellazioni, decorazioni ritmiche, i rapporti tra matematica e arte. Il ritmo complessivo del racconto giace nelle simmetrie più o meno evidenti espresse nel titolo del libro. Lo stile narrativo è accattivamente, semplice,… un libro che ci ha impressionato positivamente.
Geogebra
 Una miniguida e tanti video per imparare a usare il software open source Geogebra, un programma per l’apprendimento di geometria, algebra e analisi per la didattica della matematica nella scuola secondaria di primo e secondo grado.
Una miniguida e tanti video per imparare a usare il software open source Geogebra, un programma per l’apprendimento di geometria, algebra e analisi per la didattica della matematica nella scuola secondaria di primo e secondo grado.
Vai alla sezione di Geogebra
GeoGebra è un programma adatto per l’apprendimento di geometria, algebra e analisi. Sviluppato da Markus Hohenwarter presso la Florida Atlantic University, per la didattica della matematica nella scuola, è un sistema di geometria dinamica con il quale è possibile eseguire costruzioni con punti, vettori, segmenti, rette, coniche e funzioni e successivamente modificarle dinamicamente. Ma GeoGebra può gestire contemporaneamente variabili numeriche, vettori e punti, calcolare derivate e integrali di funzioni e dispone di comandi come Radice o Estremo. I due punti di vista, quello puramente geometrico e quello algebrico-analitico, sono caratteristici di GeoGebra: un’espressione nella finestra algebra corrisponde a un oggetto nella finestra geometria e viceversa.
La retta di Eulero di un triangolo VIDEO
In questo video si mostra come costruire con Cabri la retta di Eulero di un triangolo {flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_retta_eulero.flv{/flvremote}
77. Giochi matematici
 In questo numero: uno chef prepara un dolce, ha messo il latte in una ciotola, di quanto deve inclinare la ciotola per versare esattamente un quarto del latte contenuto? Infine un cruciverba matematico per esperti.
In questo numero: uno chef prepara un dolce, ha messo il latte in una ciotola, di quanto deve inclinare la ciotola per versare esattamente un quarto del latte contenuto? Infine un cruciverba matematico per esperti.
Parole chiave: giochi matematici, cruciverba matematico
La retta di Eulero di un triangolo
Si mostra passo passo come costruire la retta di Eulero di un triangolo con il software Cabri
1. Dall’Icona n.3 (strumenti rettilinei) attiva lo strumento "Triangolo" e disegna il triangolo:
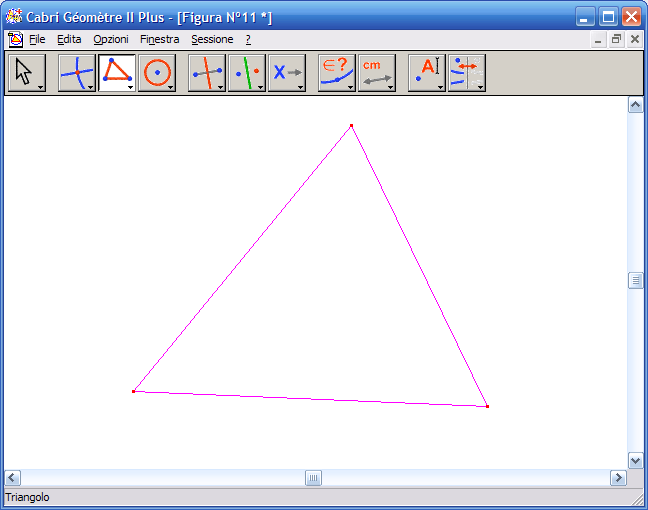
2. Dall’Icona n.5 (costruzioni) attiva lo strumento "Retta perpendicolare":
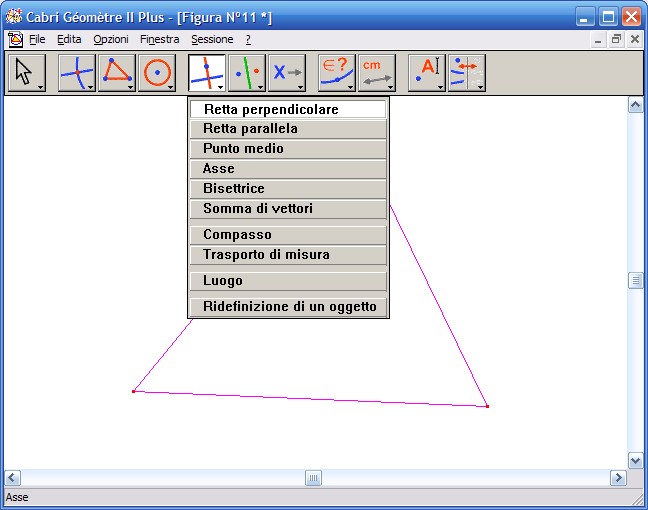
3. Fai clic su un vertice del triangolo e poi sul lato opposto, otterrai la retta dell’altezza del triangolo, ripeti l’operazione con gli altri vertici e le altre basi, otterrai le tre altezze del triangolo:
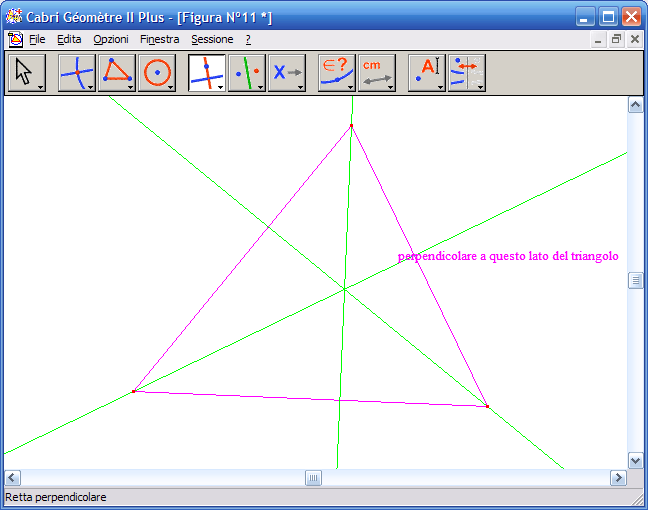
4. Dall’Icona n.2 (punti) attiva lo strumento "Punto di intersezione" e fai clic sul punto di intersezione delle altezze:
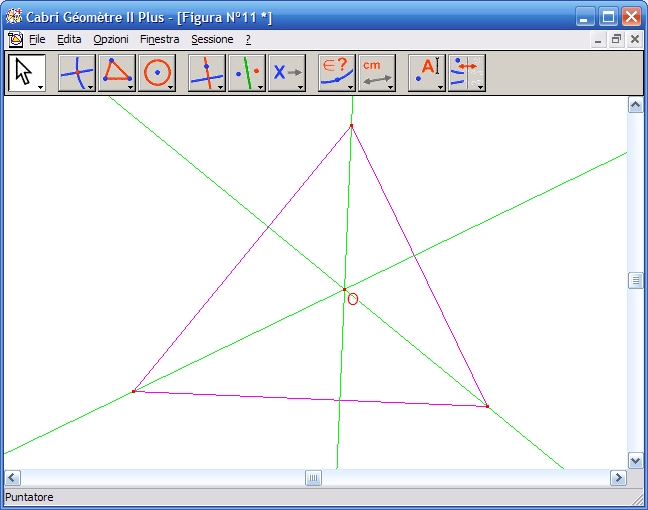
5. Dall’Icona n.11 attiva lo strumento "Mostra/Nascondi":
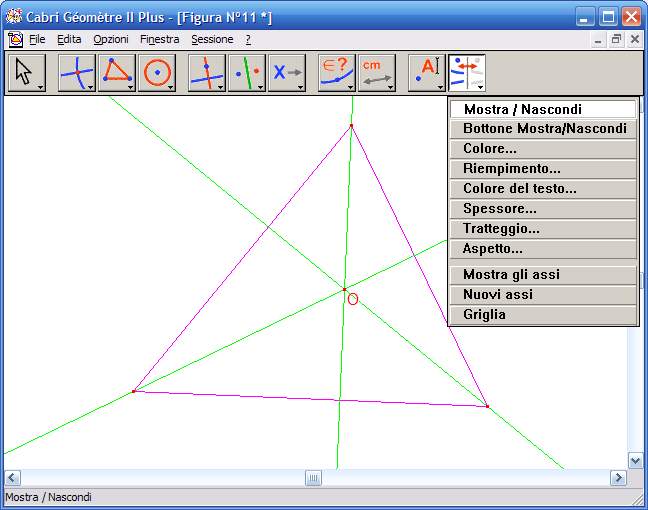
6. Fai clic sulle tre altezze per nasconderle dalla costruzione:
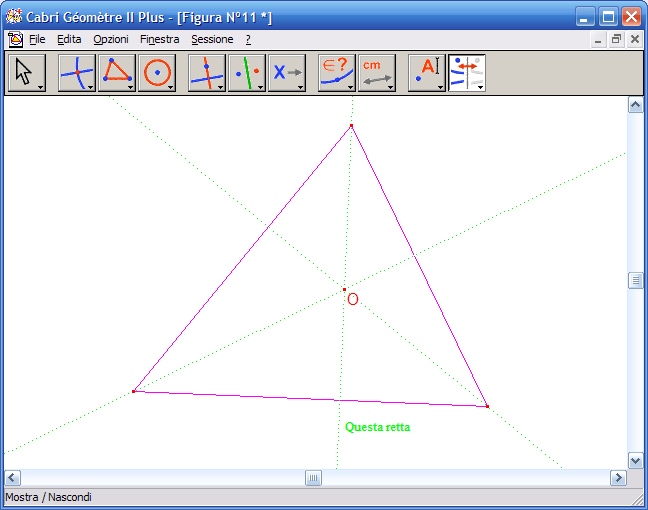
7. Dall’Icona n. 5 (costruzioni) attiva lo strumento "Punto medio":
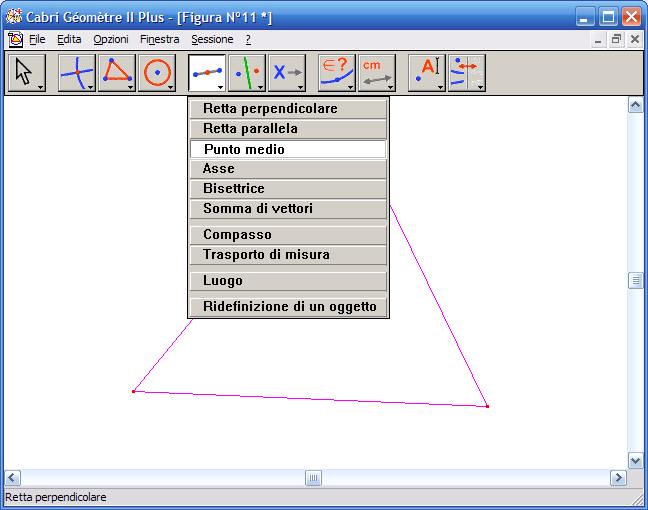
8. Con il mouse fai clic sui tre lati del triangolo per ottenere i rispettivi punti medi:
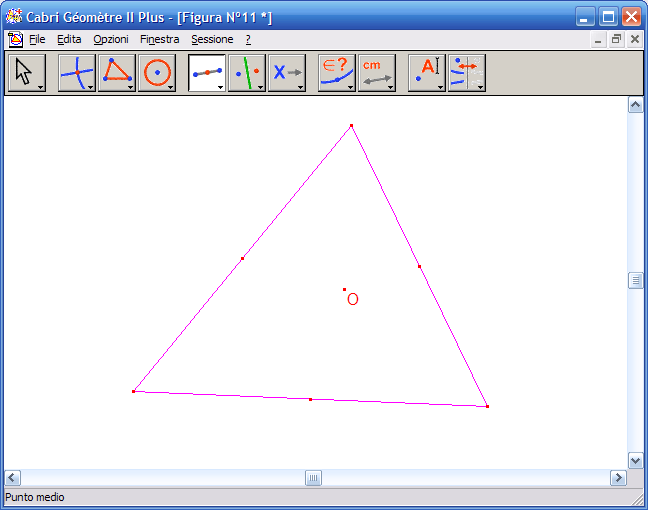
9. Dall’Icona n.3 seleziona lo strumento "Segmento":
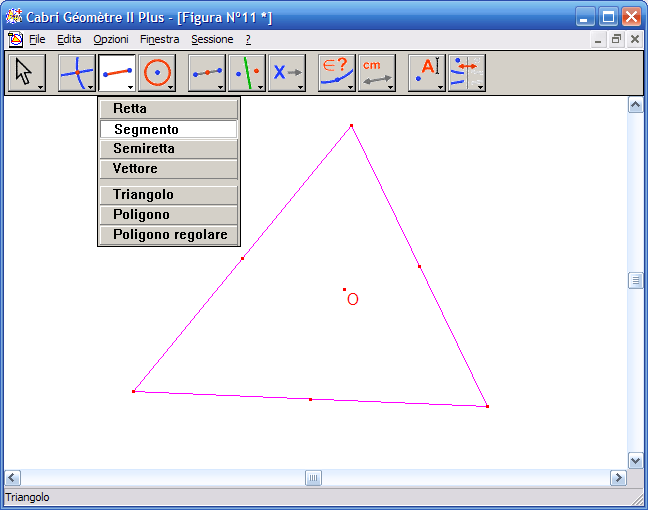
10. Fai clic su un vertice del triangolo e sul punto medio del lato opposto per ottenere la mediana; ripeti l’operazione con gli altri vertici:
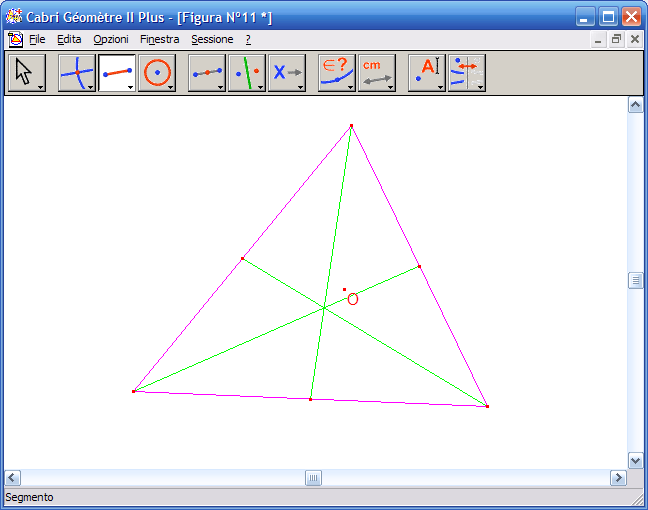
11. Dall’Icona n.2 attiva lo strumento "Punto di intersezione" e fai clic sul punto di intersezione delle tre mediane:
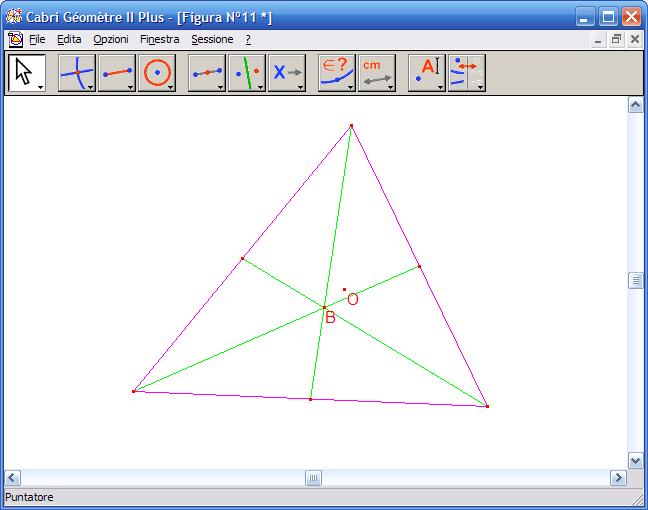
12. Attiva lo strumento "Mostra / Nascondi" e fai clic sulle mediane per nasconderle dalla costruzione:
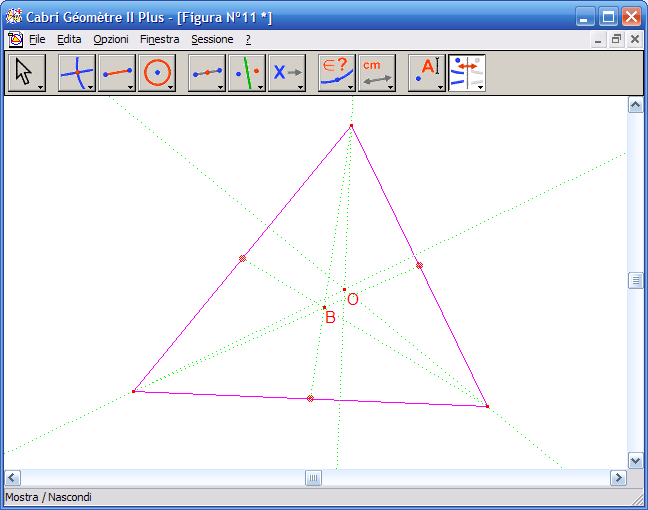
13. Dall’Icona n.5 attiva lo strumento "Asse":
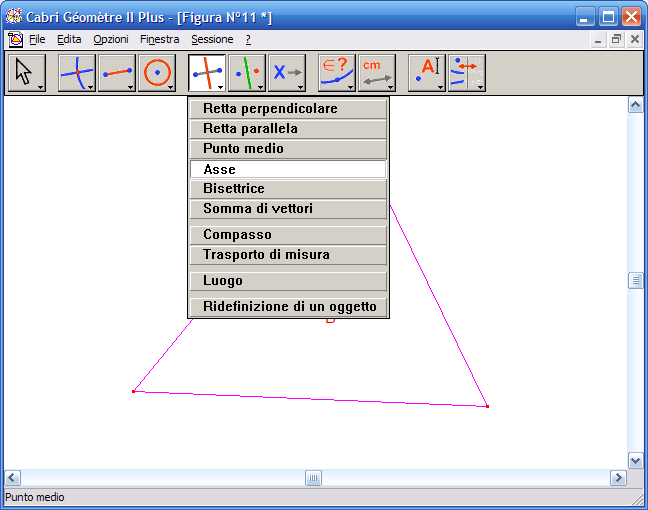
14. Fai clic su ciascuno dei tre lati del triangolo per ottenere i tre assi:
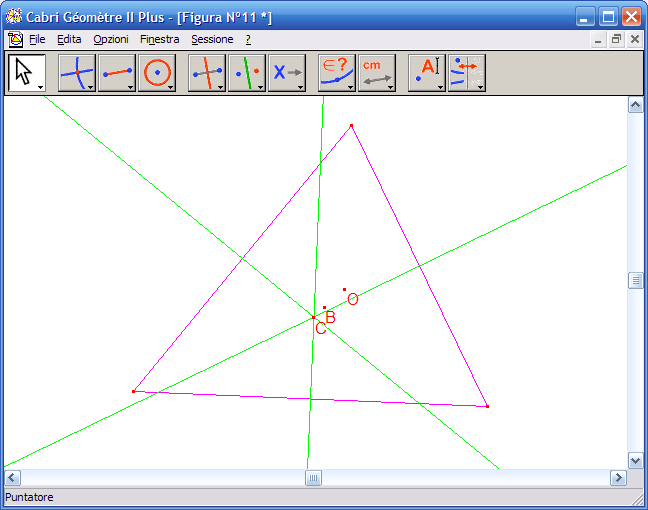
15. Con lo strumento "Punti di intersezione" fai clic sul punto di intersezione dei tre assi:

16. Con lo strumento "Mostra / Nascondi" fai clic su ciascuno dei tre assi per nasconderli dalla costruzione:
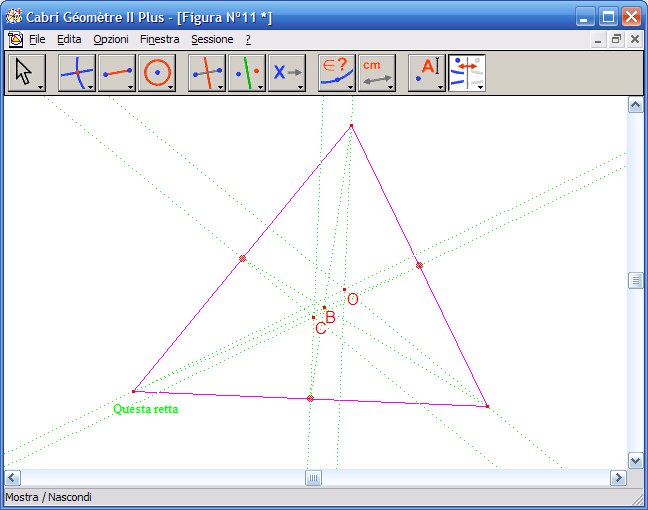
17. Dall’Icona n.3 attiva lo strumento "Retta" e fai clic su Ortocentro e Baricentro, otterrai la retta passante per questi due punti:
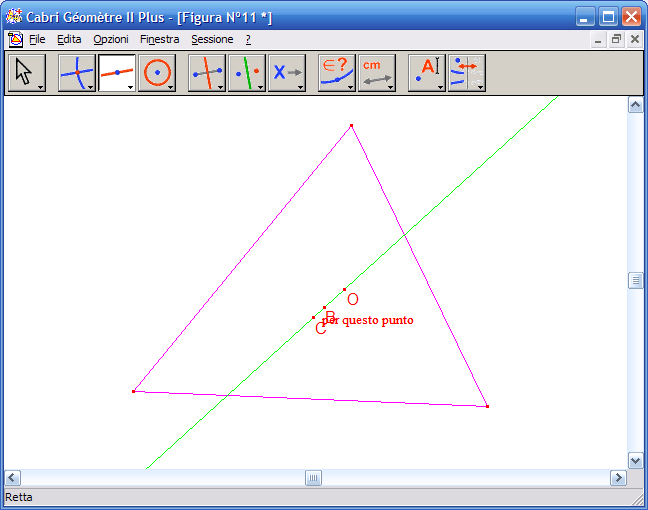
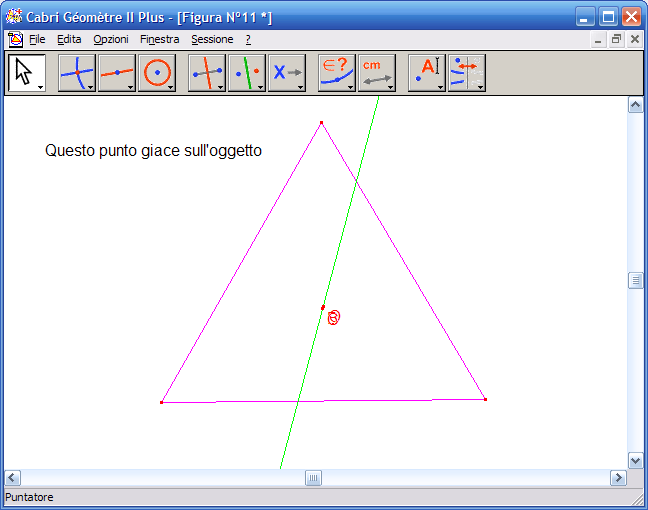
18. Dall’Icona n. 7 (relazioni) attiva lo strumento "Appartiene a…?":
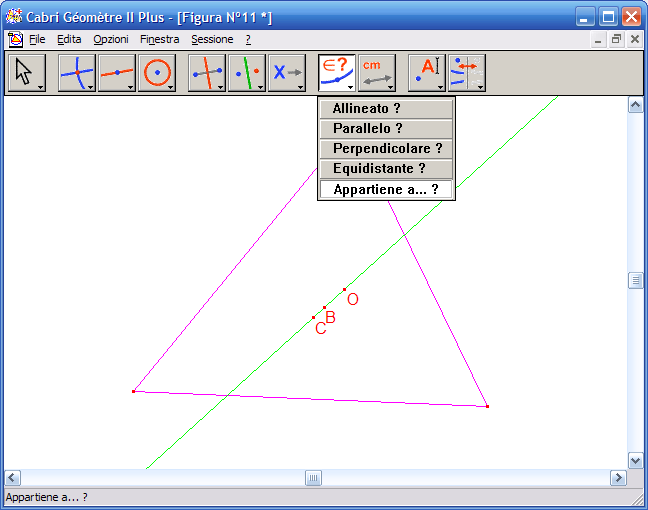
19. Fai clic sul Circocentro e poi per la retta precedentemente costruita, fai clic su un punto dell’area da disegno per avere la risposta, se la costruzione è corretta la risposta sarà: "Questo punto giace sull’oggetto". La retta costruita è quindi la retta che passa per ortocentro, baricentro, circocentro, nota con il nome retta di Eulero.
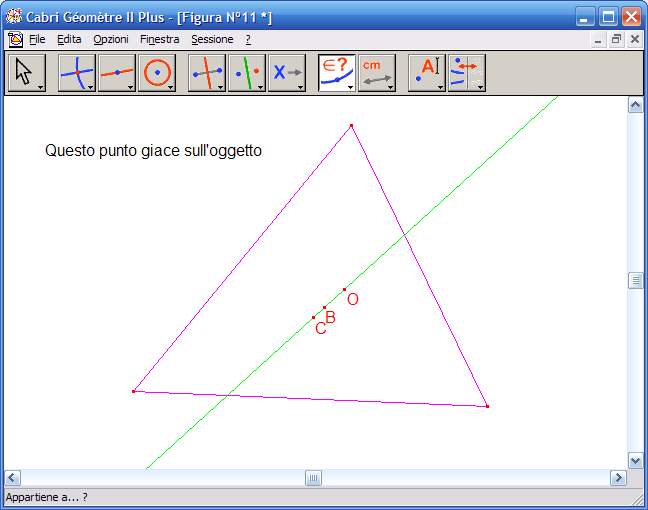
20. Con lo strumento "Puntatore" muovi uno dei vertici del triangolo fino a ottenere un triangolo rettangolo, noterai che l’ortocentro coincide con uno dei vertici del triangolo e la retta di Eulero coincide con la mediana.
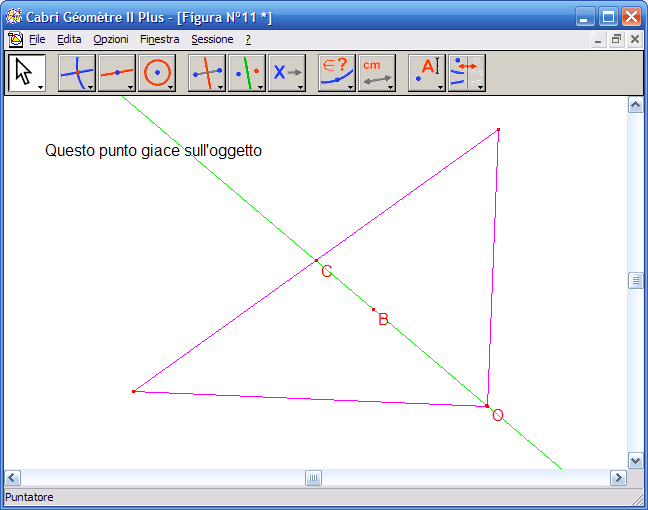
21. Continua a mouvere uno dei vertici del triangolo fino a fare in modo che i tre punti notevoli (ortocentro, baricentro e circocentro) coincidano, il triangolo ottenuto è un triangolo equilatero.
La retta di Eulero di un triangolo VIDEO
In questo video si mostra come costruire con il software open source Geogebra la retta di Eulero di un triangolo {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_retta_eulero.flv{/flvremote}
Costruire il circocentro di un triangolo VIDEO
In questo video si mostra come costruire il circocentro di un triangolo con Cabri {flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_circocentro.flv{/flvremote}
Costruire il circocentro di un triangolo VIDEO
In questo video si mostra come costruire il circocentro di un triangolo con il software open source Geogebra. {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_circocentro.flv{/flvremote}
Costruire l’incentro di un triangolo VIDEO
In questo video si mostra come costruire l’incentro di un triangolo con Cabri {flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_incentro.flv{/flvremote}
Costruire l’incentro di un triangolo VIDEO
In questo video si mostra come costruire l’incentro di un triangolo con il software open source Geogebra {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_incentro.flv{/flvremote}
Costruire il baricentro di un triangolo VIDEO
In questo video si mostra come costruire il baricentro di un triangolo con Cabri {flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_baricentro.flv{/flvremote}
Costruire il baricentro di un triangolo VIDEO
In questo video si mostra come costruire con Geogebra il baricentro di un triangolo. {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_baricentro.flv{/flvremote}
Costruire l’ortocentro di un triangolo VIDEO
In questo video si mostra come costruire l’ortocentro di un triangolo. {flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_ortocentro.flv{/flvremote}
Somma degli angoli interni di un triangolo
Si mostra passo passo come verificare con Cabri che la somma degli angoli interni di un triangolo misura 180°.
1. Attiva lo strumento "Triangolo":
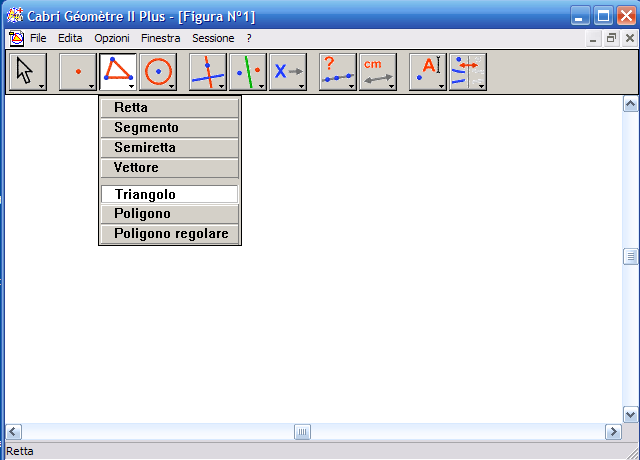
2. Per disegnare il triangolo fai clic su tre punti non allineati del piano:
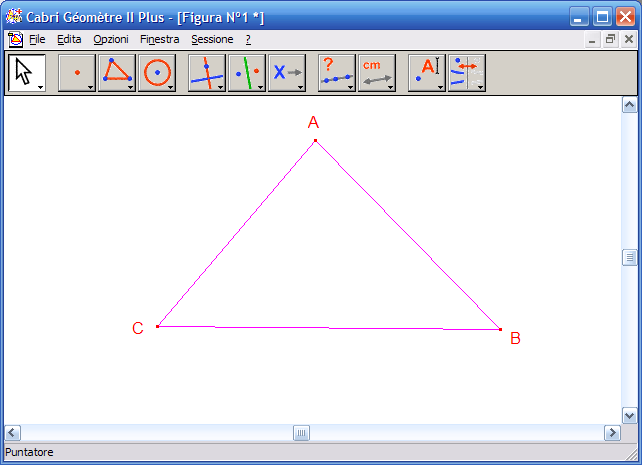
3. Attiva lo strumento "Misura dell’angolo"
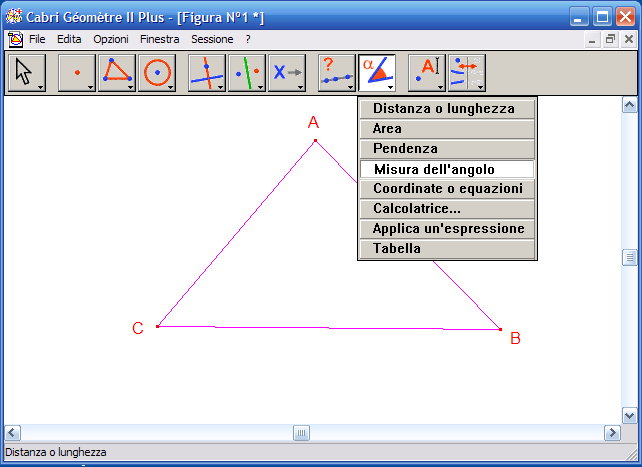
4.Fai clic in ordine sui punti B, A, C per ottenre la misura dell’angolo in A; fai clic in ordine sui punti A, B, C per ottenere la misura dell’angolo in B; fai clic in ordine sui punti B, C, A per ottenere la misura dell’angolo in C:
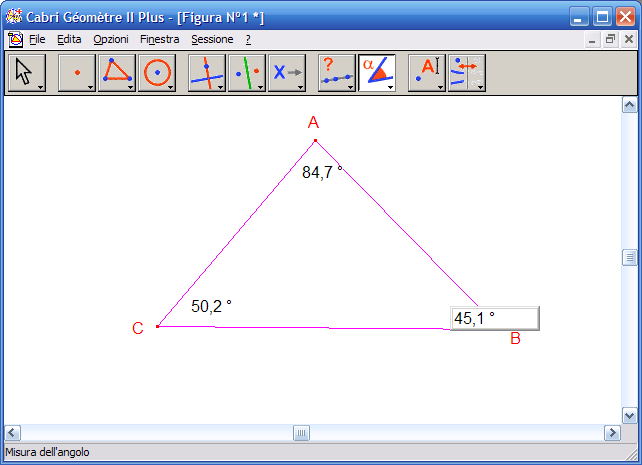
5. Dall’Icona n.9 attiva lo strumento "Calcolatrice", apparirà la finestra della calcolatrice:
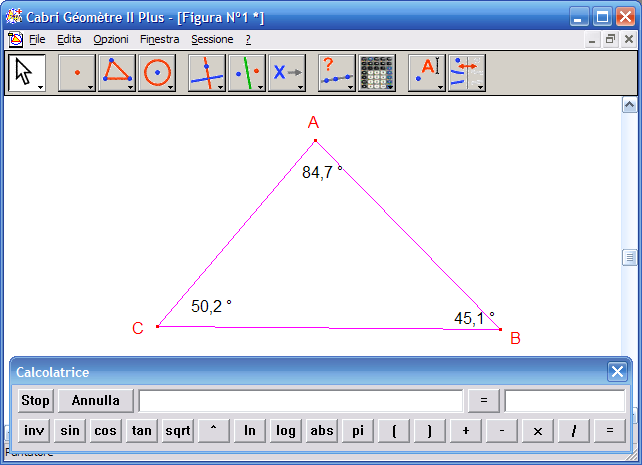
6. Fai clic in ordine sull’angolo A, sul bottone "+" della calcolatrice:
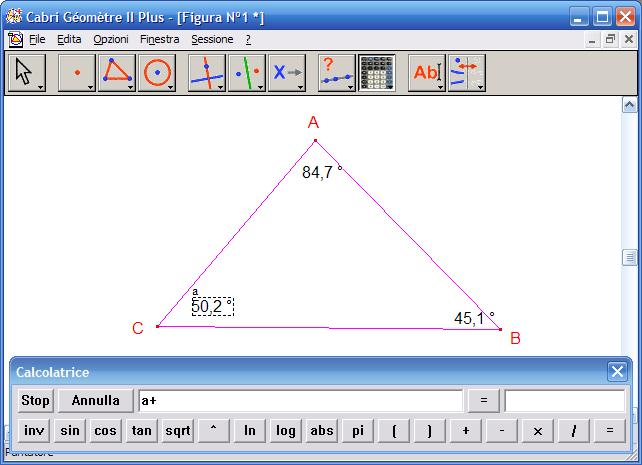
7. Fai clic sull’angolo in B, sul bottone "+" della calcolatrice, sull’angolo in C, sul bottone "=" della calcolatrice, otterrai la misura della somma degli angoli interni del triangolo, se la costruzione è corretta otterrai 180°:
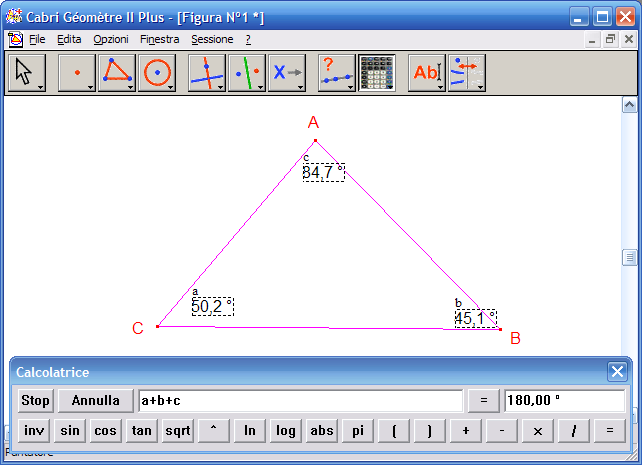
8. Puoi trascinare con il mouse il risultato della somma dalla calcolatrice al foglio da disegno:
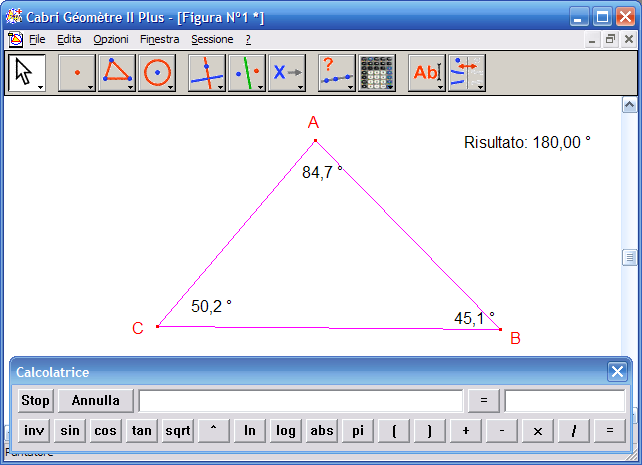
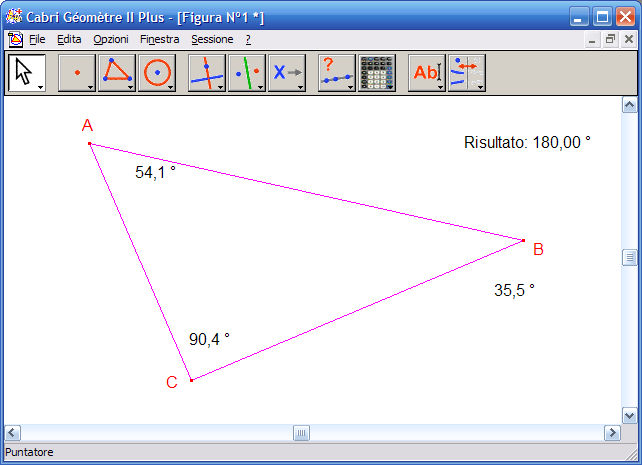
9. Con lo strumento "Puntatore" della prima Icona muovi a piacere i punti del triangolo: le misure dei singoli angoli cambieranno, la somma degli angoli resterà sempre 180°:
Costruire l’ortocentro di un triangolo VIDEO
In questo video si mostra come costruire con il software open-source Geogebra come costruire l’ortocentro di un triangolo. {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_ortocentro.flv{/flvremote}
La somma degli angoli interni di un triangolo misura 180° VIDEO
In questo video si mostra con il software Cabri che la somma degli angoli interni di un triangolo misura 180° {flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_somma_angoli.flv{/flvremote}
La somma degli angoli interni di un triangolo misura 180° VIDEO
In questo video si mostra con il software open-source Geogebra che la somma degli angoli interni di un triangolo misura 180° {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_angoli_interni.flv{/flvremote}
In un triangolo un lato è minore della somma degli altri due VIDEO
In questo video si presentano con Geogebra due proprietà relazioni tra i lati di un triangolo
{flv}triangolo_somma_lati{/flv}
Costruire l’asse di un segmento VIDEO
In questo video si mostra come costruire l’asse di un segmento con Cabri. {flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_asse_segmento.flv{/flvremote}
Costruire l’asse di un segmento
Si presenta un modo per costruire l’asse di un segmento con il software Cabri.
1. Dall’Icona n.3 attiva lo strumento "Segmenti", fai clic su due punti del piano e ottieni un segmento.
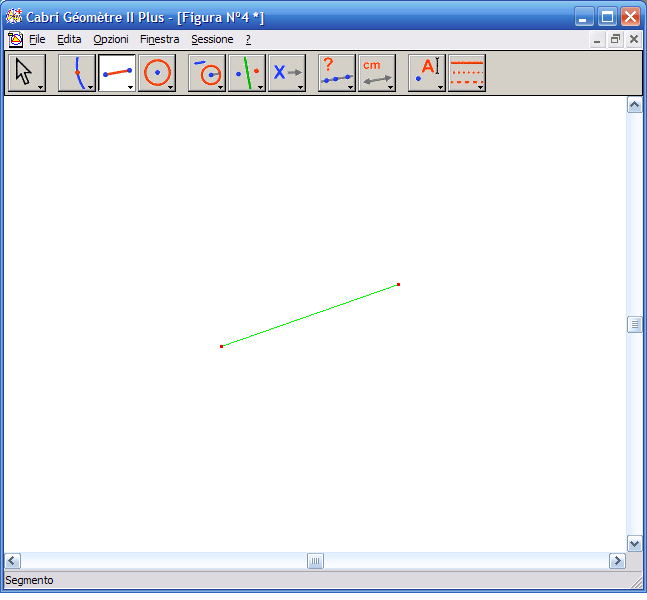
2. Dall’Icona n. 10 attiva lo strumento "Nomi", fai clic su un estremo del segmento e assegnagli il nome A, fai clic sull’altro estremo e assegnagli il nome B. Dall’Icona n.5 attiva lo strumento "Compasso", fai clic sul punto A e poi sul segmento per costruire una circonferenza di centro A e raggio AB, costruisci anche la circonferenza di centro B e raggio AB.
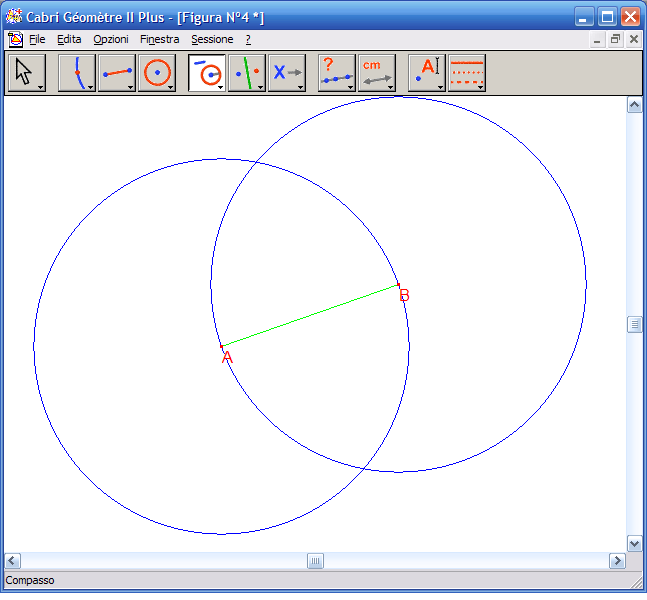
3. Dall’Icona n.2 attiva lo strumento "Intersezione di due oggetti", fai clic su ciascuno dei due punti di intersezione delle circonferenze.
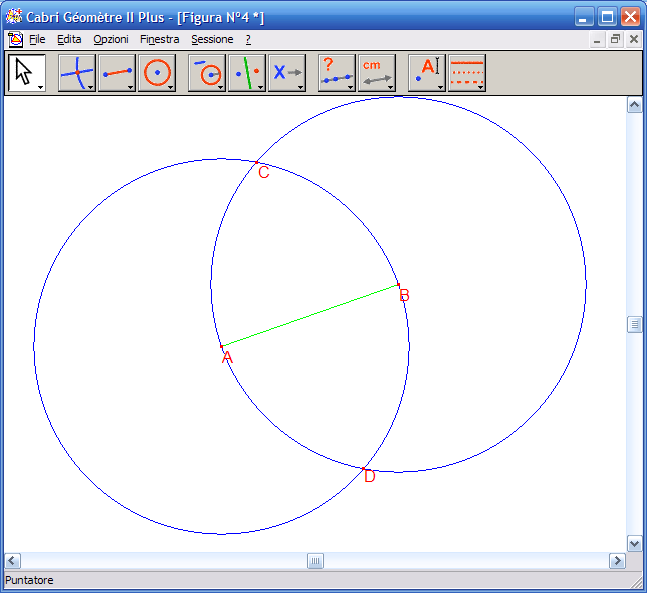
4. Dall’Icona n.3 attiva lo strumento "Retta" e fai clic sui punti C e D per ottenere la retta CD che è l’asse del segmento AB.
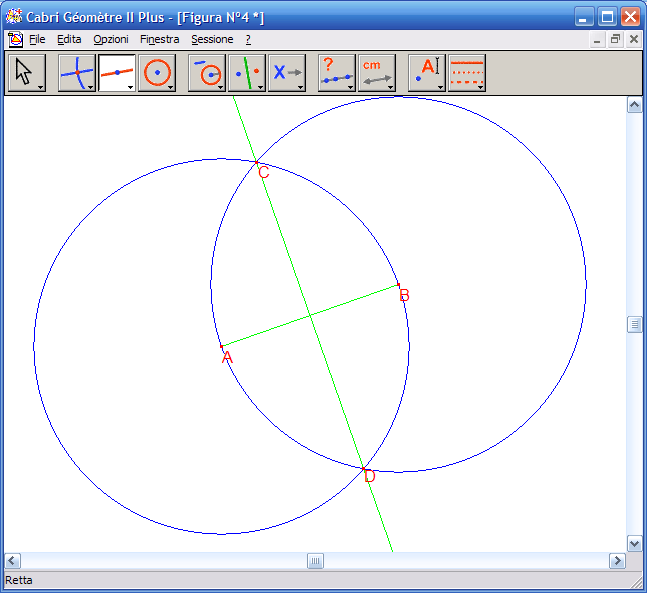
5. Verifica ora la proprietà dell’asse di un segmento, secondo la quale un qualsiasi punto dell’asse è equidistante dagli estremi del segmento. Per fare ciò dall’Icona n.2 attiva lo strumento "Punto su un oggetto" e fai clic su un punto qualsiasi della retta CD, chiama P il punto ottenuto.
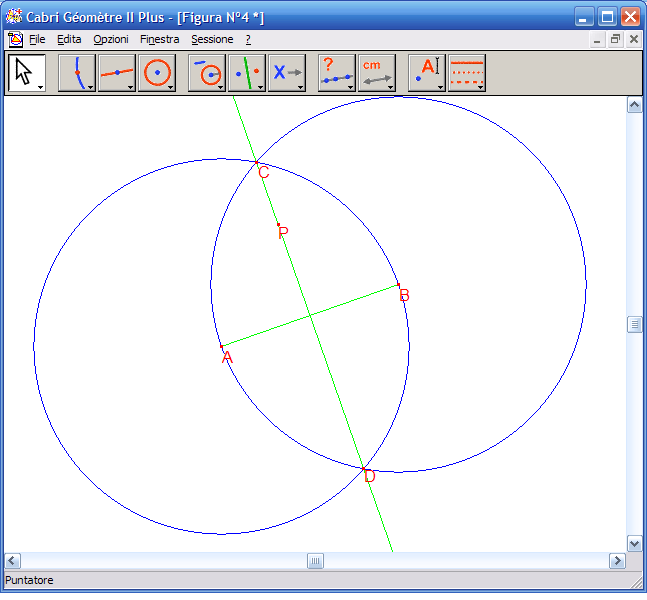
6. Per rendere più efficace la costruzione, disegna i segmenti PA e PB con lo strumento "Segmento" dall’Icona n.3. Dall’Icona n.11 attiva la modalità "Tratteggio…", scegli un tratteggio e fai clic sul segmento PA e poi su PB.
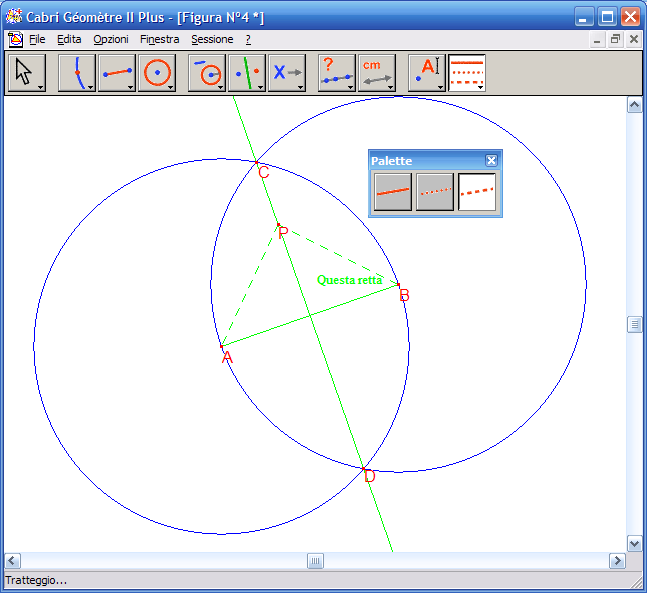
7. Dall’Icona n.9 attiva lo strumento "Distanza o lunghezza", fai clic sul segmento PA e poi su PB, se la costruzione è corretta le due distanze risulteranno uguali.
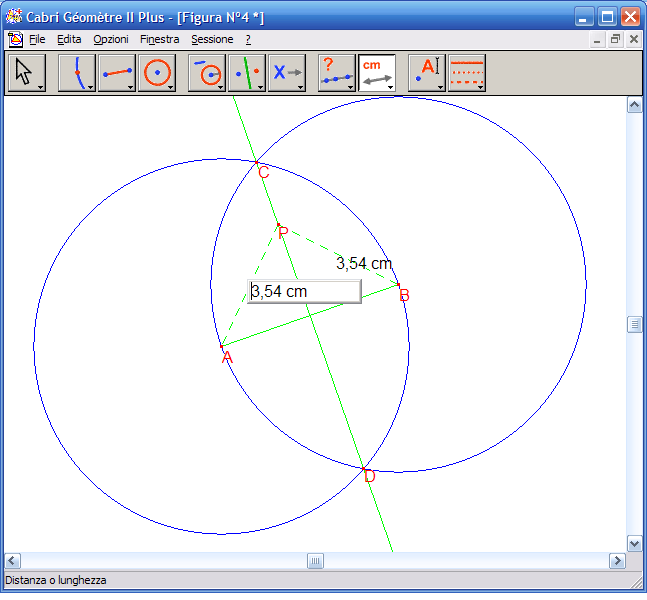
8. Dall’Icona n.1 attiva lo strumento "Puntatore" e muovi con il mouse il punto P, che resterà vincolato sull’asse: le distanze PA e PB risulteranno sempre uguali tra di loro.
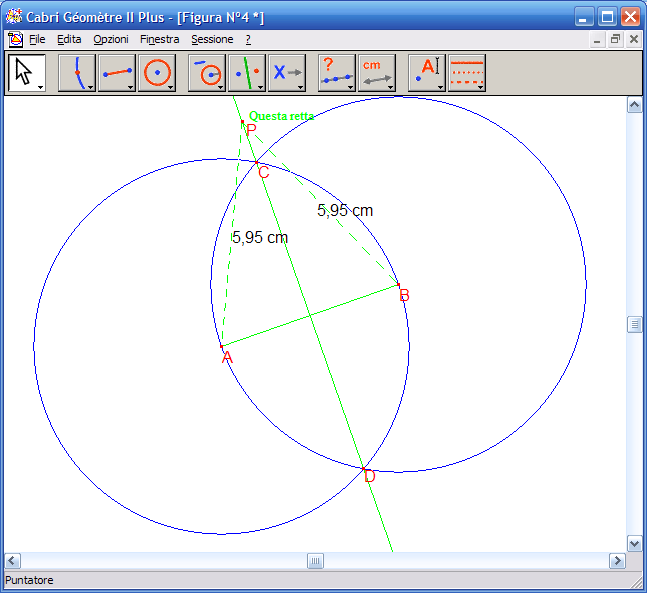
Costruire l’asse di un segmento VIDEO
In questo video si mostra come costruire l’asse di un segmento con il software Open-source Geogebra. {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_asse_segmento.flv{/flvremote}
Costruire l’asse di un segmento
Guida passo-passo per costruire l’asse di un segmento con il software open-source Geogebra.
1. Dall’Icona n.3 (strumenti rettilinei) attiva la modalità "Segmento tra due punti". Fai clic con il mouse su due punti del piano da disegno e ottieni un segmento.
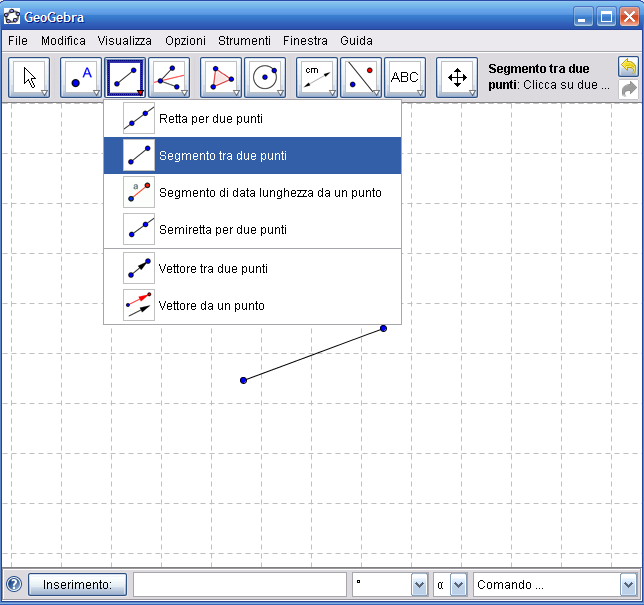
2. Dall’Icona n.10 attiva lo strumento "Mostra/nascondi etichetta" fai clic sui punti e sul segmento per visualizzare i nomi degli oggetti della costruzione.
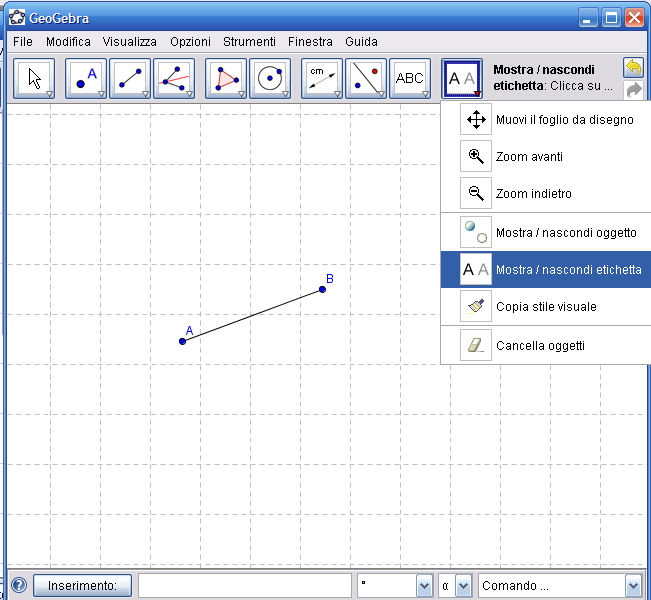
3. Dall’Icona n.6 attiva lo strumento "Circonferenza di dato centro" e disegna la circonferenza di centro A con estremo B, disegna anche la circonferenza di centro B con estremo A.
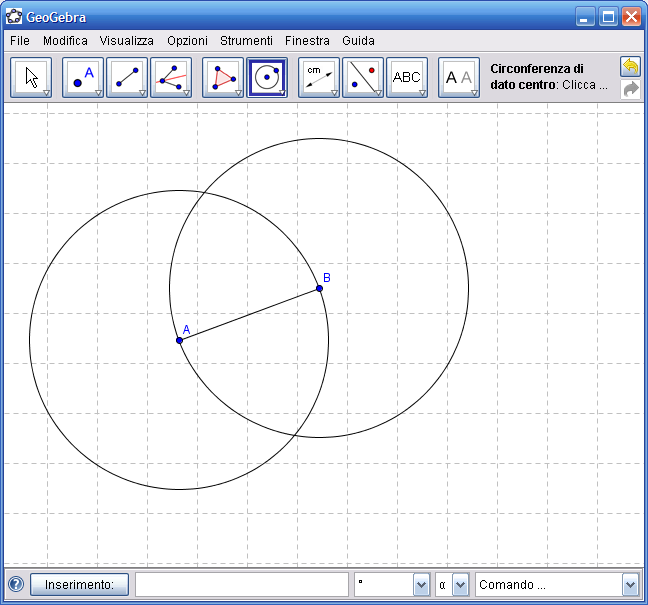
4. Dall’Icona n.2 attiva lo strumento "Intersezione di due oggetti", fai clic prima su una circonferenza e poi sull’altra, otterrai i punti C e D intersezioni delle due circonferenze
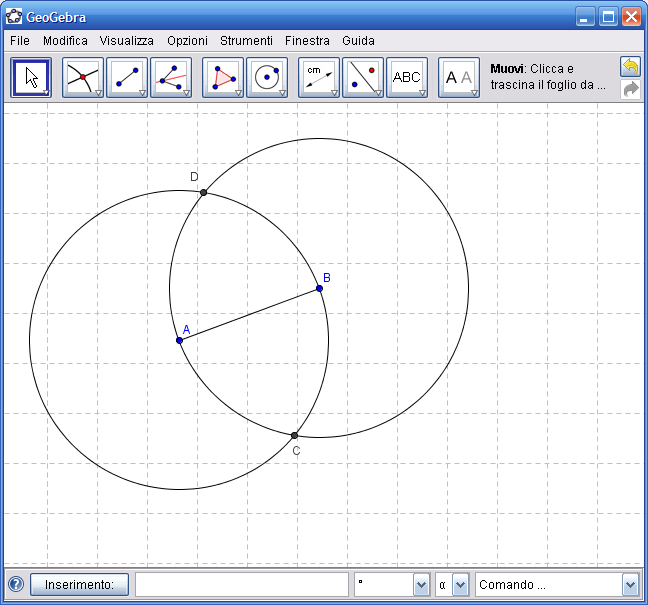
5. Dall’Icona n.3 attiva lo strumento "Retta per due punti", fai clic sul punto C e poi sul punto D, ottieni la retta CD che è l’asse del segmento AB.
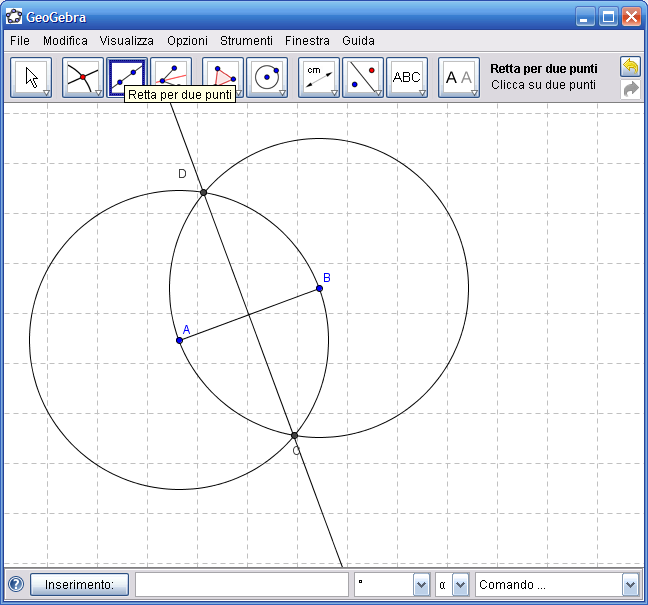
6. Verifica la seguente proprietà dell’asse di un segmento: ogni punto dell’asse è equidistante dagli estremi del segmento. Dall’Icona n. 1 attiva "Punto nuovo" e fai clic su un punto dell’asse DC, il punto E della figura che segue, questo punto resta vincolato a stare sulla retta CD.
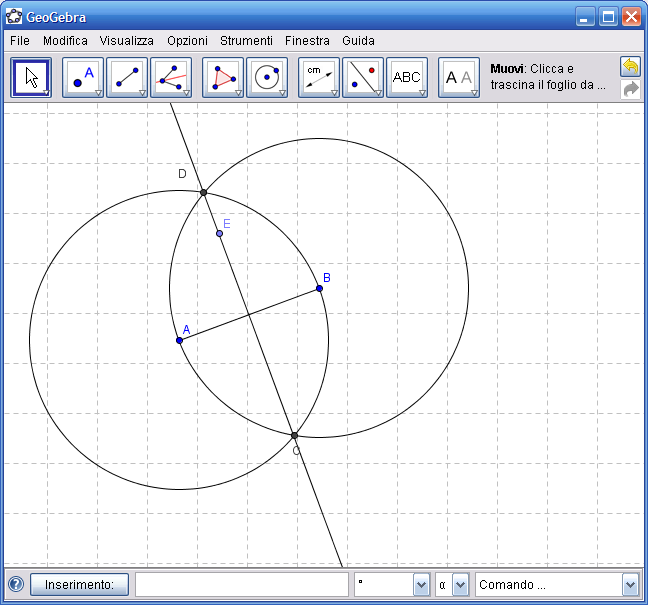
7. Dall’Icona n.7 attiva lo strumento "Distanza o lunghezza", fai clic sul punto E e poi sul punto B per ottenere la distanza EB, ripeti la stessa operazione con i punti E e A per ottenere la distanza EA. Se la costruzione è corretta le due distanze saranno uguali.
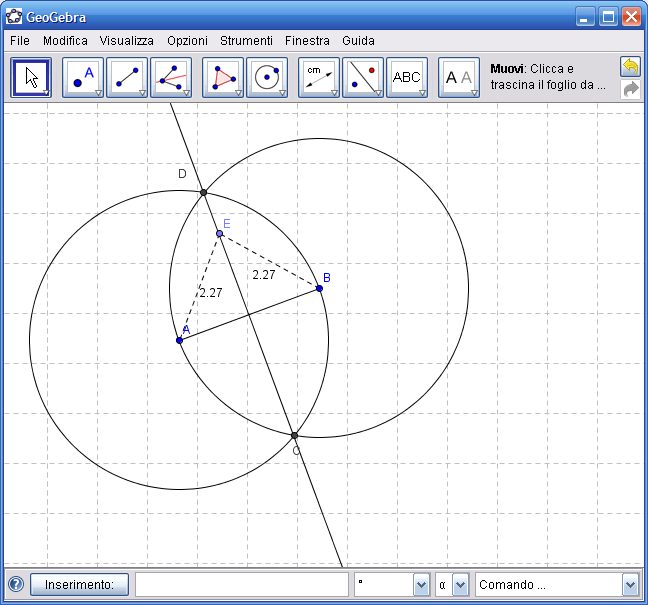
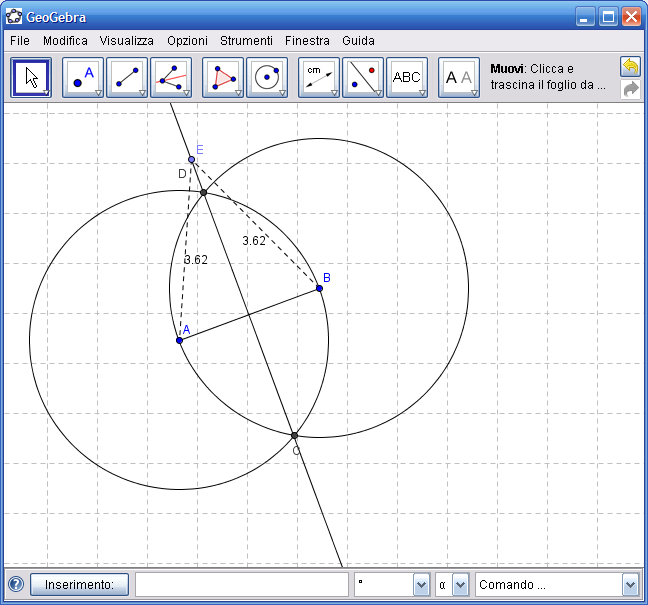
8. Dall’Icona n.1 attiva lo strumento "Muovi" e trascina con il mouse il punto E. Il punto E resterà vincolato a muoversi lungo l’asse CD e le distanze EA e EB saranno sempre uguali.
Costruire la bisettrice di un angolo VIDEO
In questo video si mostra come costruire la bisettrice di un angolo con il software open source Geogebra {flvremote}http://videolezioni.matematicamente.it/video-media/Geogebra_bisettrice.flv{/flvremote}
Costruire la bisettrice di un angolo
Si mostra come costruire la bisettrice di un angolo con il software open source Geogebra
1. Dall’Icona n.3 della barra degli strumenti, attiva lo strumento "Semiretta per due punti" e disegna le due semirette che compongono l’angolo:
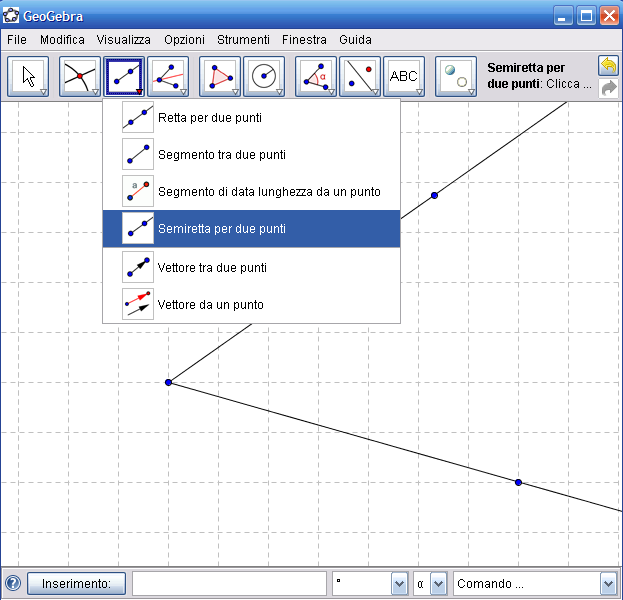
2. Dall’Icona n.5, attiva "Circonferenza di dato centro" indica il vertice dell’angolo come centro della circonferenza e poi indica un altro punto qualsiasi come secondo estremo per tracciare la circonferenza:
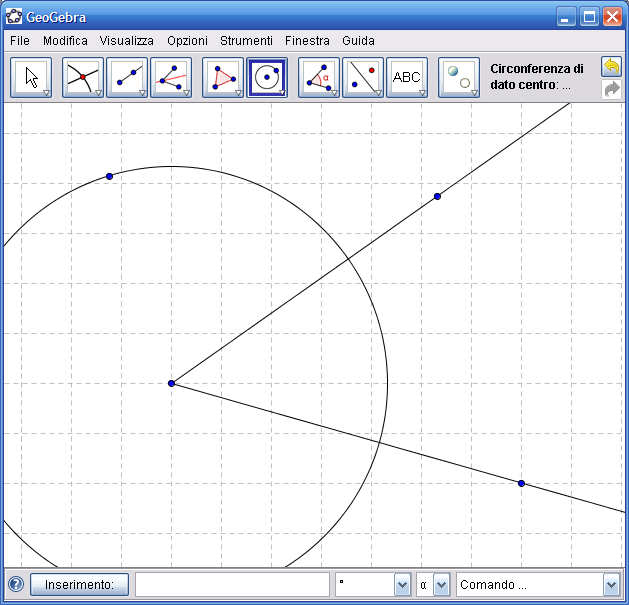
3. Dall’Icona n.2 attiva lo strumento "Intersezione di due oggetti" e segna con il mouse i due punti di intersezione della circonferenza con le semirette:
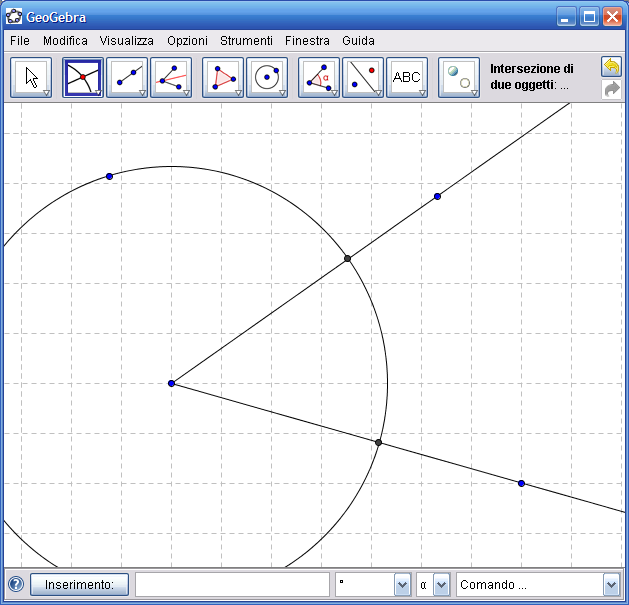
4. Dall’Icona n.5 attiva lo strumento "Circonferenza dati centro e raggio", clicca su un punto di intersezione circonferenza-semiretta, nella finestra che si apre inserisci 4 come misura del raggio:
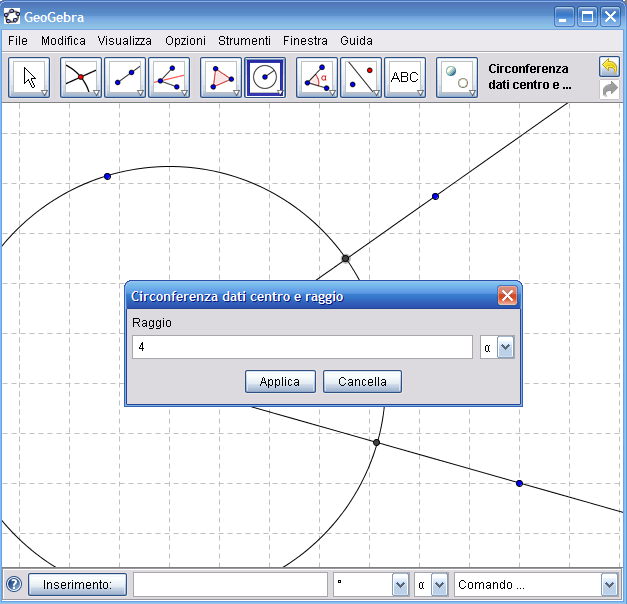
5. Ripeti il procedimento con l’altro punto di intersezione circonferenza-semiretta, avendo cura di assegnare lo stesso raggio di lunghezza 4
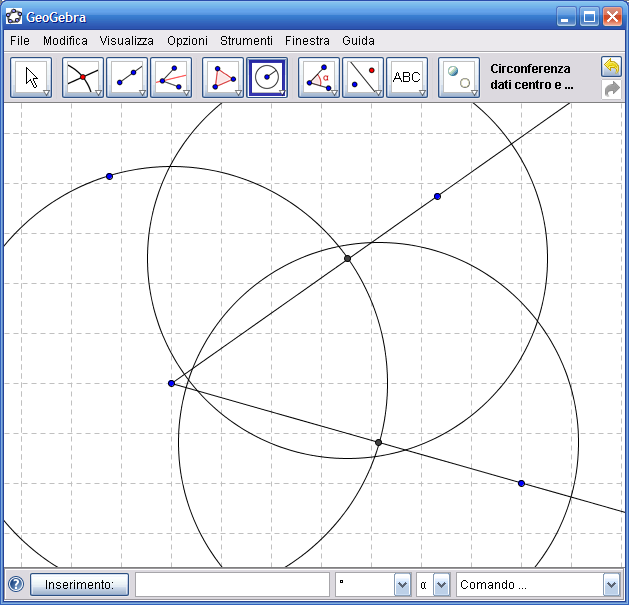
6. Dall’Icona n.2 attiva "Intersezione di due oggetti" e fai clic sul punto di intersezione delle due ultime circonferenze disegnate:
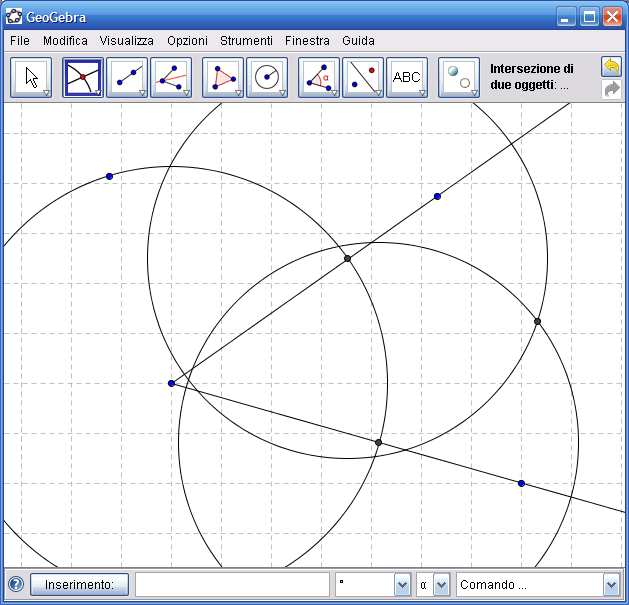
7. Dall’Icona n.3 attiva "Semiretta per due punti" e traccia la semiretta che ha origine nel vertice dell’angolo e passa per il punto ottenuto al passo precedente:
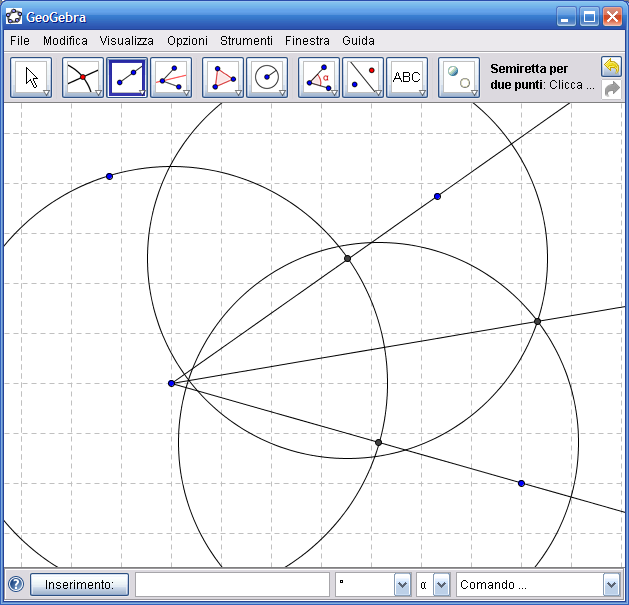
8. Dall’Icona n.10 attiva "Mostra/Nascondi oggetto" e clicca con il mouse sugli elementi della costruzione da nascondere, fino a lasciare soltanto i due lati dell’angolo e la bisettrice:
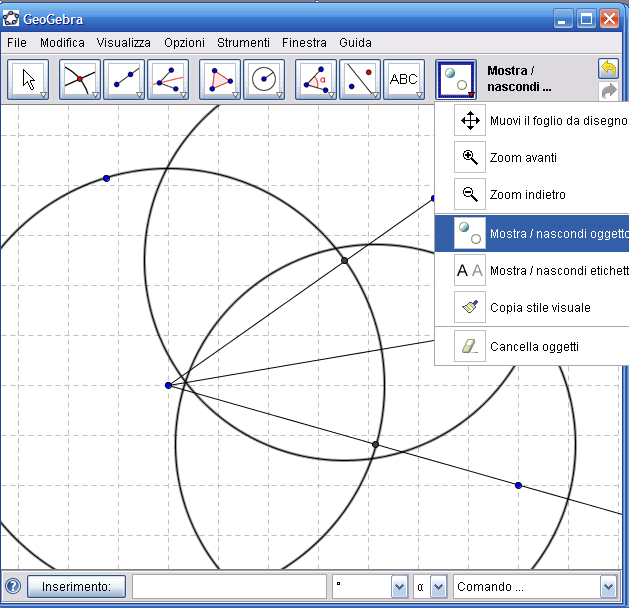
9. Fai clic sull’Icona n.1 e gli elementi indicati al passo precedente saranno nascosti:
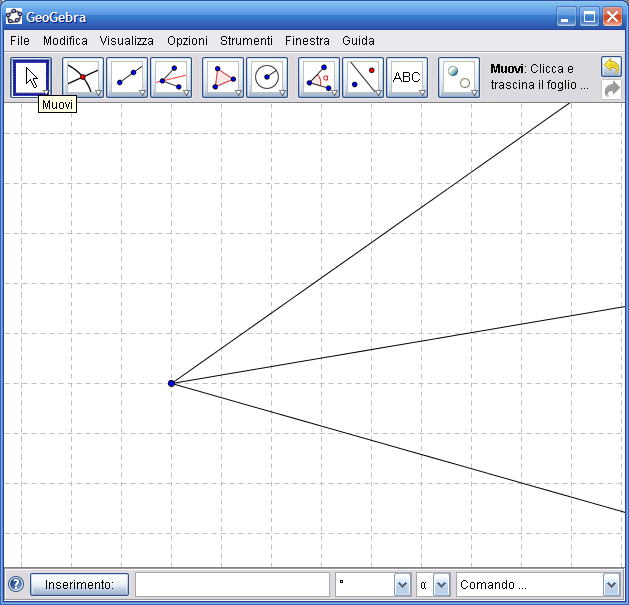
10. Dall’Icona n.7 attiva lo strumento "Angolo" e fai clic prima su una delle due semirette e poi sulla bisettrice, in questo modo verrrà indicato l’angolo compreso tra le due semirette e sarà indicata anche la misura dell’angolo. Se viene indicato l’angolo concavo invece di quello convesso, puoi modificare questa scelta facendo clic con il tasto destro del mouse sull’angolo e dal menu contestuale che appare scegli la voce "Proprietà", come mostrato in figura:
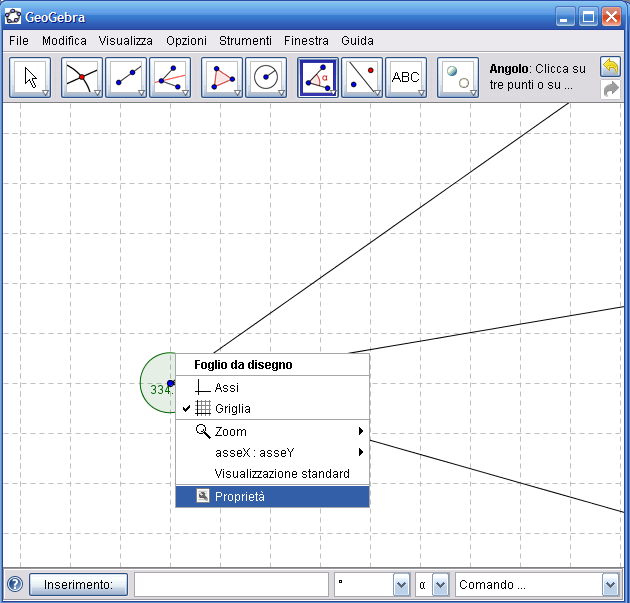
11. Nella successiva finestra che si apre, togli la spunta alla voce "permetti angolo concavo"
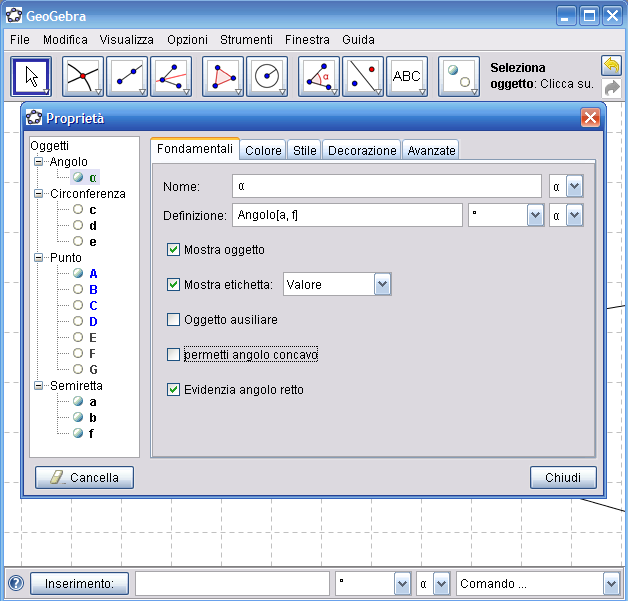
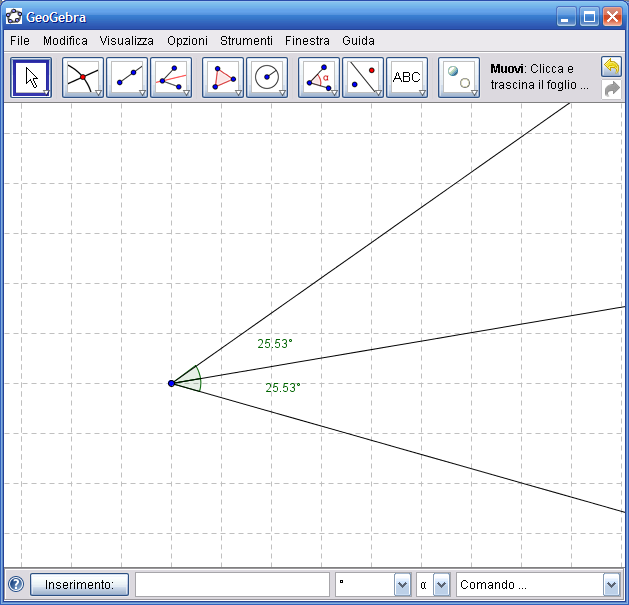
12. Ripeti lo stesso procedimento per l’altro angolo. Se la costruzione è stata effettuata correttamente le misure dei due angoli risulteranno uguali:
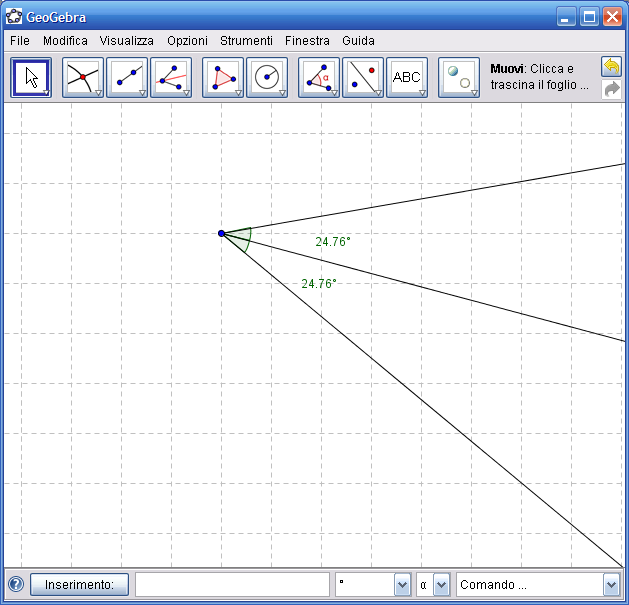
13. Infine dall’Icona n.1 attiva lo strumento "Muovi" e con il mouse trascina il vertice dell’angolo: l’angolo cambierà di dimensioni ma la bisettrice continuerà a dividerlo sempre in due parti uguali.
Costruire la bisettrice di un angolo VIDEO
In questo video si mostra come costruire la bisettrice di un angolo con il software Cabri Géométre II Plus
{flvremote}http://videolezioni.matematicamente.it/video-media/Cabri_bisettrice.flv{/flvremote}
Costruire la bisettrice di un angolo
Come si costruisce la bisettrice di un angolo con Cabri Géométre II plus
1. Disegno dell’angolo – Dalla barra degli strumenti, attiva lo strumento "Semiretta" e traccia due semirette con l’origine in comune:
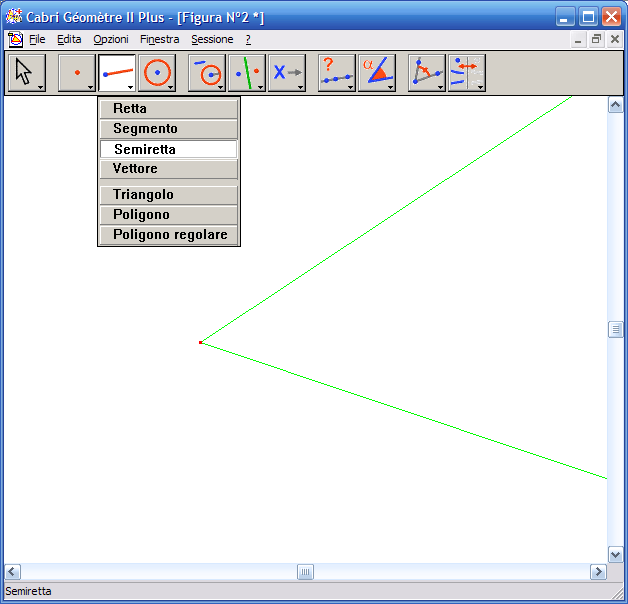
2. Disegna una circonferenza con centro l’origine delle semirette e raggio a piacere – Con lo strumento "Circonferenza" indica prima il centro della circonferenza, che sarà l’origine delle bisettrici, e poi un altro estremo qualsiasi:
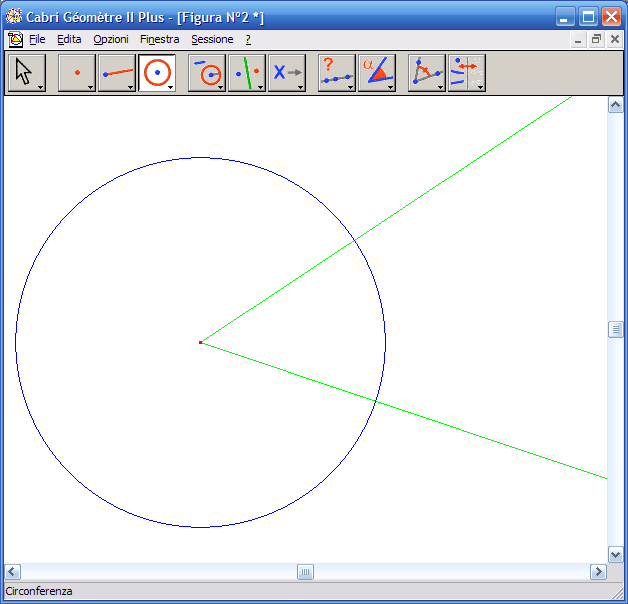
3. Segna i punti di intersezione della circonferenza con le semirette – Attiva lo strumento "Intersezione di due oggetti" e indica con il cursore il punto di intersezione della circonferenza con una semiretta, fai clic con il tasto sinistro del mouse; indica con il cursore il punto di intersezione della circonferenza con l’altra semiretta.
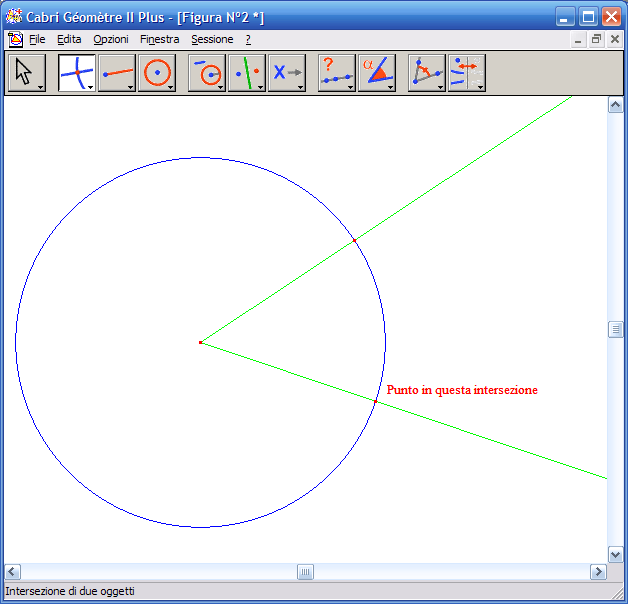
4. Disegna un segmento – Con lo strumento segmento traccia un segmento che sarà il raggio delle due circonferenze che occorrerà disegnare:
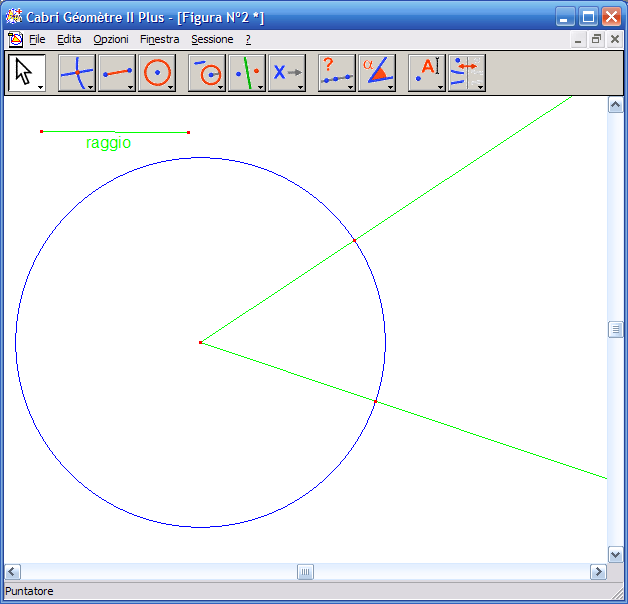
5. Con lo strumento "Compasso" traccia una circonferenza con il centro nel punto di intersezione individuato al punto 4 e raggio il segmento tracciato; traccia l’altra ciconferenza con centro nell’altro punto di intersezione e lo stesso raggio. Con lo strumento "Intersezione di due oggetti" marca il punto di intersezione delle due circonferenze:
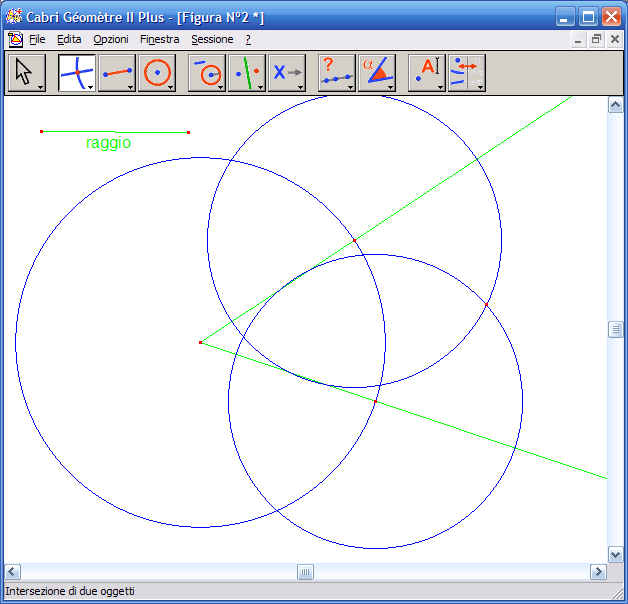
6. Con lo strumento "Semiretta" disegna la semiretta passante per il vertice dell’angolo e per il punto di intersezione delle due circonferenze:
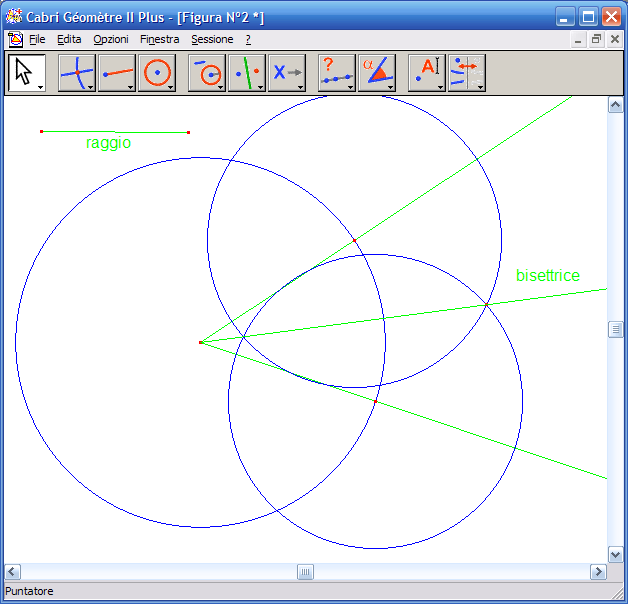
7. Con lo strumento "Mostra nascondi" nascondi tutti gli elementi della costruzione, in modo che restino soltanto i lati dell’angolo e la bisettrice:
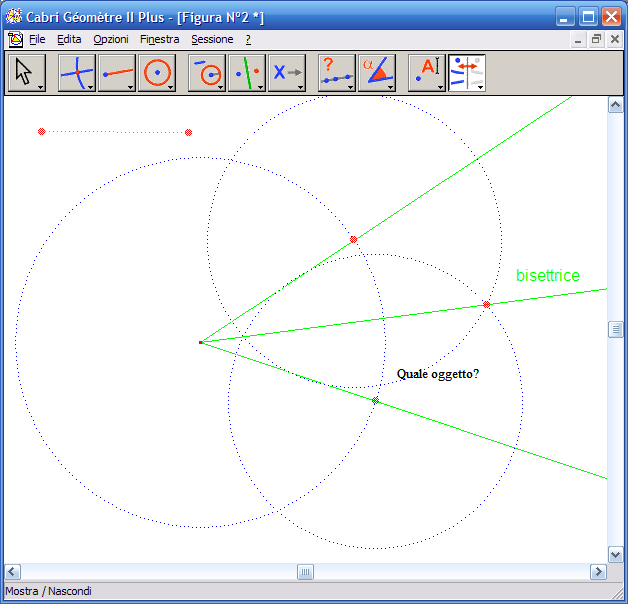
8. Con lo strumento "Misura dell’angolo" indica in ordine un punto del lato dell’angolo, il vertice dell’angolo, un punto della bisettrice: otterrai come risultato la misura di uno dei due angoli. Ripeti lo stesso procedimento per ottenere la misura dell’altro angolo. I due angoli risulteranno della stessa misura:
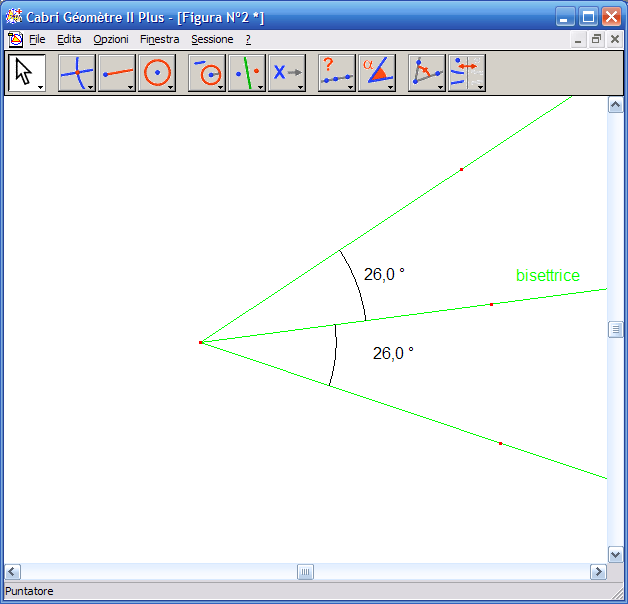
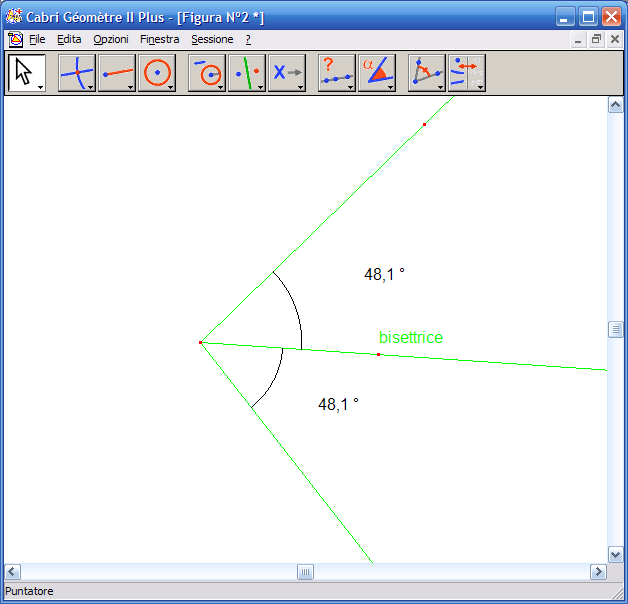
9. Attiva lo strumento "Puntatore" e con il mouse muovi i lati dell’angolo: le dimensioni dell’angolo varieranno ma la bisettrice tracciata individua sempre due angoli congruenti.
Passeggiate aleatorie
 Una passeggiata aleatoria è un percorso dove ogni passo ha una direzione casuale e possibilmente anche una dimensione casuale. Queste passeggiate aleatorie, a caso, servono come modelli per studiare fenomeni variabili come la diffusione, l’altalena dei valori di borsa, ecc.
Una passeggiata aleatoria è un percorso dove ogni passo ha una direzione casuale e possibilmente anche una dimensione casuale. Queste passeggiate aleatorie, a caso, servono come modelli per studiare fenomeni variabili come la diffusione, l’altalena dei valori di borsa, ecc.
Dimostrazione dell’irrazionalità di e
 In questa nota si dimostra che il numero di Nepero "e" è irrazionale. La dimostrazione richiede conoscenze di matematica superiore.
In questa nota si dimostra che il numero di Nepero "e" è irrazionale. La dimostrazione richiede conoscenze di matematica superiore.
Policultura: concorso per scuole primarie, secondarie di primo e secondo grado
 Per prendere parte a PoliCultura, occorre iscriversi e realizzare una narrazione multimediale attraverso il software "1001storia", messo a disposizione gratuitamente dal Politecnico di Milano.
Per prendere parte a PoliCultura, occorre iscriversi e realizzare una narrazione multimediale attraverso il software "1001storia", messo a disposizione gratuitamente dal Politecnico di Milano.
http://www.policultura.it/concorso.htm
PoliCultura si divide in 3 concorsi:
PoliCultura SENIOR (scuole secondarie di secondo grado)
PoliCultura JUNIOR (scuole secondarie di primo grado)
PoliCultura KIDS (scuole primarie)
PoliCultura SENIOR, dedicato alle scuole secondarie di secondo grado, si divide in 3 sezioni, a seconda del tema che si sceglie di trattare:
“Le tue radici”. Un argomento di rilievo per il territorio in cui si trova la scuola (storia, arte o tradizioni).
“Il tempo”. Rintracciare lungo la storia del pensiero umano come esso sia stato influenzato da diverse concezioni del tempo; individuare e commentare in particolare come il tempo sia considerato nella fisica e nelle scienze naturali e come, da queste e dalla visione matematica e filosofica, esso sia diventato un parametro essenziale nelle tecnologie elettroniche, informatiche e delle telecomunicazioni (tema proposto dalla facoltà dell’Ingegneria dell’Informazione del Politecnico di Milano).
Tema libero: Un argomento legato al programma scolastico di qualsiasi materia, anche scientifica, che si vuole approfondire.
In PoliCultura JUNIOR e PoliCultura KIDS (per le scuole primarie), le tematiche possono essere le più svariate, in ambito umanistico o scientifico (descrizione di un esperimento, di una scoperta, spiegazione di formule matematiche ecc.). La tematica scelta potrà riguardare anche più materie contemporaneamente, oppure si potrà raccontare un’uscita didattica o un progetto realizzato a scuola.
Le modalità dei tre concorsi sono descritte in modo particolareggiato nei rispettivi siti:
http://www.policultura.it/senior/home.htm
Video lezioni
CruciPuzzle – Natale 2007
 Un crucipuzzle per il Natale. Trova nello schema tutte le parole di matematica elencate … e scopri la frase misteriosa.
Un crucipuzzle per il Natale. Trova nello schema tutte le parole di matematica elencate … e scopri la frase misteriosa.
Pagina Web creata con Crossword Compiler.
Il Piacere di Insegnare – Il Piacere di Imparare la Matematica
 CONVEGNO NAZIONALE
CONVEGNO NAZIONALE
San Giovanni Valdarno – Montevarchi – Terranuova Bracciolini – Figline Valdarno
21 – 22 – 23 febbraio 2008
Gentile collega, non accade spesso, nel panorama italiano dell’educazione scolastica, che più scuole di tipo diverso, appartenenti a comuni diversi e situati anche in province diverse, si mettano, come si dice oggi, in rete, per organizzare un convegno nazionale che faccia il punto su quanto di meglio è stato prodotto in Italia nella "Didattica della matematica e nei processi di apprendimento".
Attraverso numerosi incontri svoltisi durante tutto il 2007 nelle varie sedi delle scuole organizzatrici, siamo pervenuti alla formulazione del programma del convegno "Il Piacere di Insegnare – Il Piacere di Imparare la Matematica" che si svolgerà nei giorni 21, 22 e 23 febbraio 2008 nei comuni del Valdarno: San Giovanni Valdarno, Montevarchi, Terranuova Bracciolini e Figline Valdarno.
Al convegno sono stati invitati, come relatori, i maggiori esperti del panorama nazionale nella didattica della matematica, provenienti dalle più prestigiose università italiane, da numerose istituzioni e scuole superiori e dell’obbligo di tutta Italia.
Il convegno costituisce anche un’occasione per far conoscere ad insegnanti provenienti da tutte le regioni d’Italia le ricchezze storico-artistico-ambientali della nostra vallata e delle tre città d’arte che la circondano: Firenze, Arezzo e Siena.
Puoi trovare il programma e tutte le informazioni sul sito internet
http://www.liceisgv.it/convegno/
Con preghiera di massima diffusione della presente email, ti ringraziamo, ti salutiamo e ti aspettiamo in Valdarno.
Il Comitato Scientifico e Organizzatore:
per la scuola dell’Infanzia, Primaria e Secondaria di primo grado, Anna Gloria Giorgi, Marialaura Lapucci
per la scuola Secondaria di secondo grado, Gabriele Baldi, Silvana Bianchini, Attilio Ferrini, Francesca Lascialfari

