Convegno e corso di aggiornamento per docenti di matematica sui temi della nuova didattica per la matematica: giochi, modelli e tecnologie.
Convegno e corso di aggiornamento per docenti di matematica sui temi della nuova didattica per la matematica: giochi, modelli e tecnologie.
26-27-28-29 marzo 2008, Duomo Antico, Milazzo (ME)
Il Comune di Milazzo in rete con le scuole,
organizza il Meeting Mylaematica
sul tema
Giochi, Modelli e Tecnologie per la Nuova Didattica della Matematica
26-27-28-29 marzo 2008, Duomo Antico, Milazzo (ME)
con il patrocinio di Dipartimento di Matematica Università di Messina, AIF Sezione di Messina, Mathesis
Comitato Scientifico
Primo Brandi (U Perugia), Luisa Carini (U Messina), Mauro Cerasoli (U Roma 3), Francesco A. Costabile (U Calabria), Andrea Laforgia (U Roma 3), Domenico Lenzi (U Lecce), Annarosa Serpe (U Calabria)
Comitato Organizzatore
Cinzia Catanzaro, Mauro Cerasoli, Teresa D’Andrea, Mario Gregorio, Alessandra La Camera, Eugenio Mercuri, Adele R. Ruggeri, Daniela Smedile
Programma
Mercoledì 26 marzo
15:00 Iscrizioni, saluto delle autorità e apertura del convegno
15:40 Luisa Carini (U Messina) Algebra interattiva
16:20 Comunicazioni
17:00 Intervallo
17:20-19:00 Tavola rotonda dei docenti partecipanti al Corso di Formazione Primaria (a cura di Mat^Nat Matematica in Natura)
Giovedì 27 marzo
9:00 Alessandro Sarritzu (U Messina) Matematica e Musica: una proposta didattica
9:20 Giuseppe Gentile (U Messina) Gli ostacoli epistemologici: dalla Storia alla Didattica
10:00 Renato Migliorato (U Messina) Dalla visione mitica alla visione scientifica: un percorso per la Didattica
10:40 Cinzia Catanzaro (IC S. Lucia del Mela ME) MaD: Matematica a distanza
11:00 Intervallo
11:20 Comunicazioni
12:00 Edoardo Piparo (LS Messina) Dal gioco della vita di Conway al calcolatore universale
12:20 Comunicazioni
13:00 Intervallo pranzo
15:00 Franca Rossetti (ITIS Monza) Motivazioni didattiche a partire da un problema di Eulero
15:20 Rosanna Utano (U Messina)
16:00 Francesco A. Costabile, Annarosa Serpe (U Calabria) Il calcolatore nella Scuola Primaria: una proposta per attività logico-matematico-linguistiche
17:00 Intervallo
17:20 Mauro Cerasoli (U Roma 3) La stocastica di TI-nspire
18:00 Comunicazioni
18:40-19:00 Massimo Raffa (LC Milazzo) Symphonoi arithmoi: musica e matematica nel pensiero greco
Venerdì 28 marzo
9:00 Comunicazioni
10:20 Domenico Lenzi (U Lecce) La modularità in aritmetica e in altri contesti
11:00 Intervallo
11:20 Primo Brandi (U Perugia) Matematica & media
12:00 Anna Salvadori (U Perugia) I saperi del cittadino: i modelli matematici in elettricità (dalla pila di Volta all’effetto foto-voltaico)
12:40 Comunicazione
13:00 Intervallo pranzo
15:00 Andrea Laforgia (U Roma 3) Per divertirsi con l’Analisi
15:40 Bruno Barigelli, Paolo Bruni (U Ancona) Esperienza in classe di un nuovo modello per lo studio degli sforzi tangenziali nel moto laminare
16:20 Mauro Francaviglia, Marcella G. Lorenzi (U Calabria) Arte per una matematica divertente
17:00 Intervallo
17:20 Domenico Cariello (LS Salerno) Modelli esponenziali e logaritmici con TI-nspire CAS
18:00 Laura Persico (LS Giarre) La divertimatica (fare Matematica divertendosi)
18:20 Giovanni Corrado (LS Catanzaro)
18:40-19:00 Giuseppe Sollami (LS Caltanissetta) Matematica per lottatori di sumo
20:30 Cena di gala
Sabato 29 marzo
9:00 Alessandra Provenzano (LC Palermo) Retta, parabola e frattali come strumenti di modellizzazione della vita reale
9:20 Lucia Perretti (ITC Potenza) Ascoltando i modelli
9:40 Anna Alfieri (LS Catanzaro) Trasformazioni geometriche e frattali IFS
10:00 Tiziana Bindo (MPI) Curve celebri disegnate con TI-nspire
10:30 Domenica di Sorbo (DS Sparanise CE) Il ruolo delle tecnologie nella didattica: come e perché
11:00 Intervallo 11.20 Salvatore D’Arrigo (LS Messina) Origami e matematica: l’arte di piegare la carta come attività ludo-didattica
12:00 Carmelo Di Stefano (LS Gela) Insegnare matematica con TI-nspire
12:40 Giovanni Florio (LS Messina) Presentazioni on screen e didattica della matematica
13:00 Intervallo pranzo
15:00-18:00 La didattica informale e lo sviluppo delle intelligenze multiple di Howard Gardner attraverso l’uso di exhibit (modelli scientifici sperimentali realizzati con materiale povero, a cura di Salvatore D’Arrigo)
Informazioni
Chi desidera tenere una comunicazione di 20 minuti può fare la richiesta a [email protected] inviando il titolo e un sunto di una pagina entro il 29 febbraio 2008. L’iscrizione avviene durante il convegno; sono gradite le prenotazioni a [email protected] . Ai partecipanti che non sono relatori o iscritti alla SISSIS è richiesto un contributo alle spese di organizzazione di 30€ (ridotto a 20€ per i soci di ADT, AIF, Mathesis, Mat^Nat).
ADT rilascerà un attestato di partecipazione ad aggiornamento in base alla CM 376, prot. 15218, del 23-12-1995 e successive modifiche.
Al fine di seguire i lavori del convegno, il MPI concede l’esonero dal servizio per insegnanti di ogni ordine e grado, per il personale direttivo e ispettivo.
E’ prevista la pubblicazione degli atti.
Nel pomeriggio di sabato 29 marzo si svolgerà la finale delle Gare di Matematica con le Tecnologie. Bando e regolamento sul sito www.adt.it (Info: [email protected] ). Soggiorno Informazioni sugli alberghi sono sul sito www.milazzohotel.com
Contattare [email protected] per le prenotazioni.
 Modelli di regressione per fattori controllabili non lineari nei parametri: possibili contributi della Geometria Differenziale. Tesi di Laurea per il Corso di Laurea Specialistica in Scienze Statistiche ed Economiche Indirizzo per il Controllo della Qualità ed il Marketing, Università cattolica del sacro cuore di Milano. La tesi tratta dell’utilizzo della metodologia geometrico-differenziale in ambito di analisi dei modelli statistici non lineari. L’autore ha iniziato un dottorato di ricerca in Statistica.
Modelli di regressione per fattori controllabili non lineari nei parametri: possibili contributi della Geometria Differenziale. Tesi di Laurea per il Corso di Laurea Specialistica in Scienze Statistiche ed Economiche Indirizzo per il Controllo della Qualità ed il Marketing, Università cattolica del sacro cuore di Milano. La tesi tratta dell’utilizzo della metodologia geometrico-differenziale in ambito di analisi dei modelli statistici non lineari. L’autore ha iniziato un dottorato di ricerca in Statistica. 
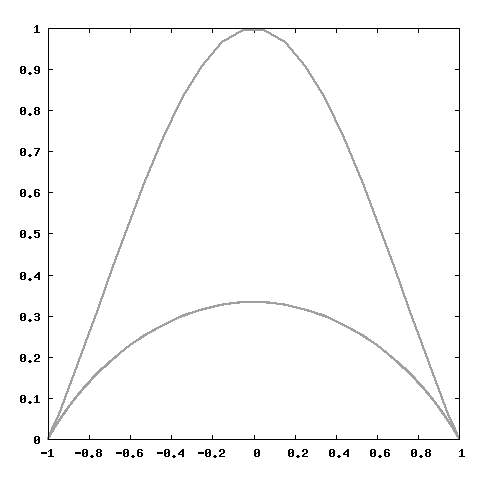
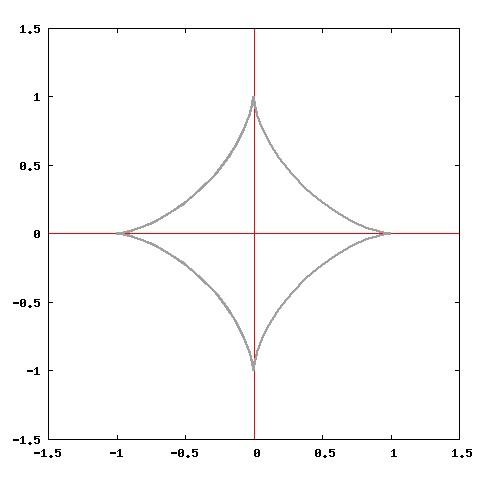
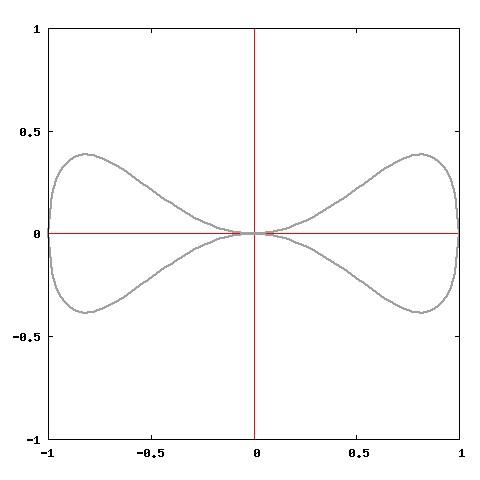
 In questo gioco devi scegliere una carta tra quelle che ti propongo, osservarla e memorizzala; un algoritmo sarà in grado di individuarla e di toglierla dal mazzo. Provare per credere. La teoria degli insiemi la farà sparire!
In questo gioco devi scegliere una carta tra quelle che ti propongo, osservarla e memorizzala; un algoritmo sarà in grado di individuarla e di toglierla dal mazzo. Provare per credere. La teoria degli insiemi la farà sparire! 
 Nicoletta Passera insegna matematica nella scuola secondaria di primo grado "Ardigò" di Monza. Nel laboratorio di matematica ha proposto una ricerca sugli studi che i matematici hanno fatto su uno dei numeri più noti della matematica $pi$ pi greco, ecco come i ragazzi hanno interpretato il compito.
Nicoletta Passera insegna matematica nella scuola secondaria di primo grado "Ardigò" di Monza. Nel laboratorio di matematica ha proposto una ricerca sugli studi che i matematici hanno fatto su uno dei numeri più noti della matematica $pi$ pi greco, ecco come i ragazzi hanno interpretato il compito.  Un file di Excel realizzato dai ragazzi dell’Istituto Comprensivo di Muro Leccese (sede di Palmariggi) per il calcolo di perimetro e area delle principali figure geometriche piane. Il file, utile per risolvere esercizi di geometria, è un esempio didattico di uso di Excel nell’insegnamento della matematica per la secondaria di primo grado.
Un file di Excel realizzato dai ragazzi dell’Istituto Comprensivo di Muro Leccese (sede di Palmariggi) per il calcolo di perimetro e area delle principali figure geometriche piane. Il file, utile per risolvere esercizi di geometria, è un esempio didattico di uso di Excel nell’insegnamento della matematica per la secondaria di primo grado. 
 Incontro su Matematica e Biomedicina – Venerdì 8 febbraio 0re 16.00 – presso Politecnico di Torino – Aula Magna G.Agnelli – Corso Duca degli Abruzzi, 24 – Torino
Incontro su Matematica e Biomedicina – Venerdì 8 febbraio 0re 16.00 – presso Politecnico di Torino – Aula Magna G.Agnelli – Corso Duca degli Abruzzi, 24 – Torino  L’Istituto storico italiano per il medioevo e la Società italiana di scienze matematiche e fisiche Mathesis, in collaborazione con il Ministero della Pubblica Istruzione, bandiscono un concorso dal titolo La matematica nel Medioevo, destinato agli studenti delle scuole secondarie di secondo grado.
L’Istituto storico italiano per il medioevo e la Società italiana di scienze matematiche e fisiche Mathesis, in collaborazione con il Ministero della Pubblica Istruzione, bandiscono un concorso dal titolo La matematica nel Medioevo, destinato agli studenti delle scuole secondarie di secondo grado.  Il titolo completo di questa tesi di laurea in Ingegneria Elettronica è "Analisi e controllo di sistemi non lineari con applicazione ad un Robot sottoattuato". Nella prima parte, si introducono i principali risultati della Teoria dei Sistemi Dinamici non lineari. Nella seconda parte della tesi universitaria, l’autore presenta un controllore per un sistema sottoattuato: il sistema "Pendubot", formato da un doppio pendolo di cui il primo braccio è attuato, cioè è collegato ad un motore elettrico, mentre il secondo è libero di muoversi.
Il titolo completo di questa tesi di laurea in Ingegneria Elettronica è "Analisi e controllo di sistemi non lineari con applicazione ad un Robot sottoattuato". Nella prima parte, si introducono i principali risultati della Teoria dei Sistemi Dinamici non lineari. Nella seconda parte della tesi universitaria, l’autore presenta un controllore per un sistema sottoattuato: il sistema "Pendubot", formato da un doppio pendolo di cui il primo braccio è attuato, cioè è collegato ad un motore elettrico, mentre il secondo è libero di muoversi.  Un test con 30 domande sui limiti notevoli sul calcolo di limiti immediati. Sono gli esercizi sui limiti che è necessario conoscere per risolvere tutti i limiti in matematica.
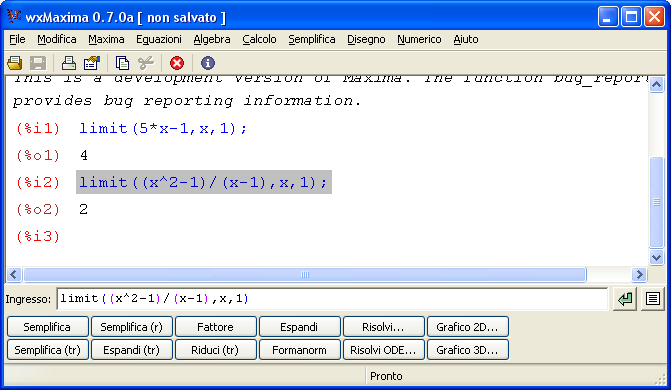
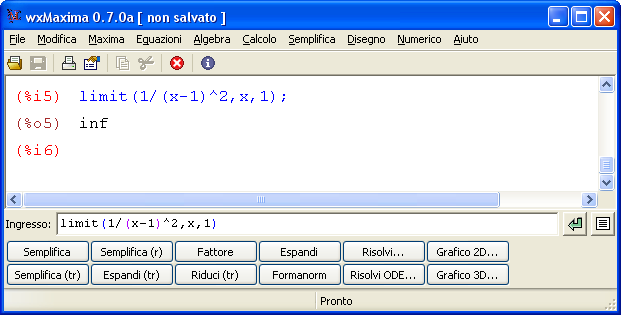
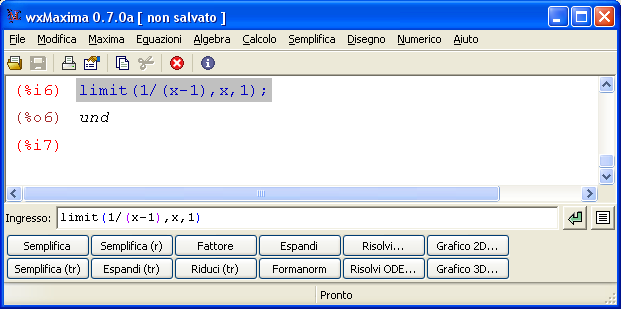
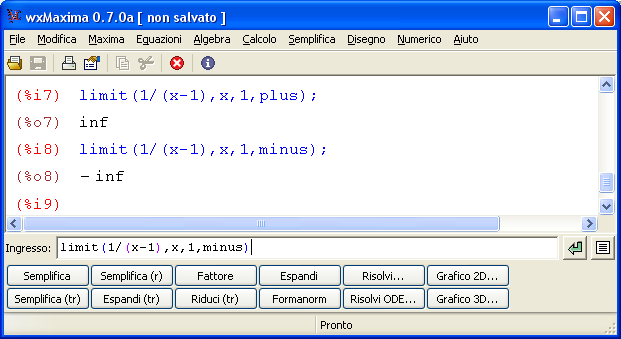
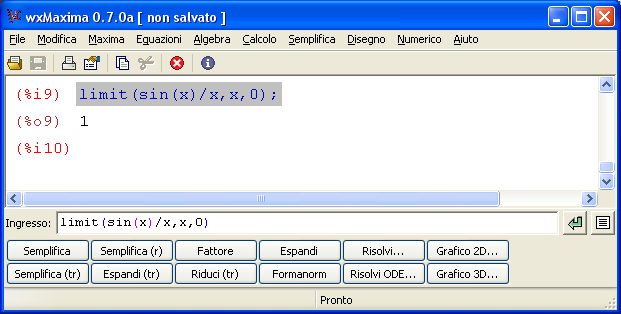
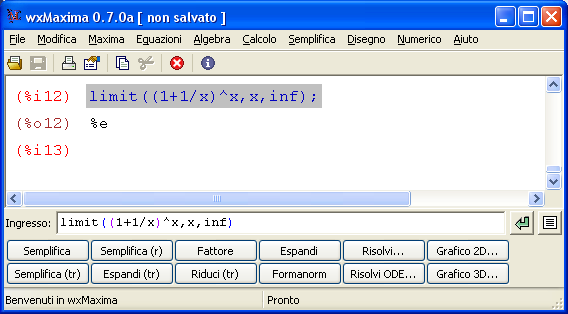
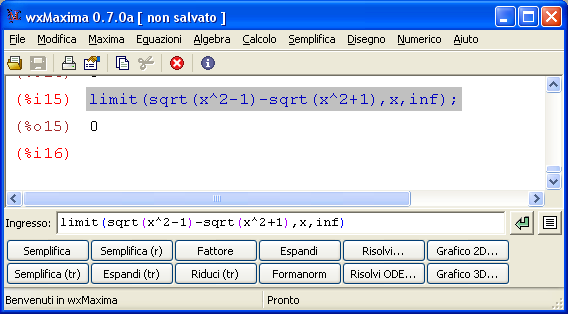
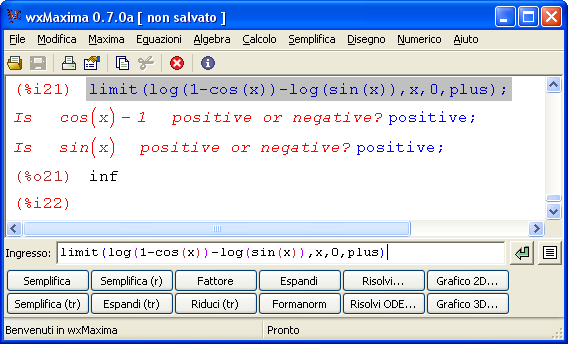
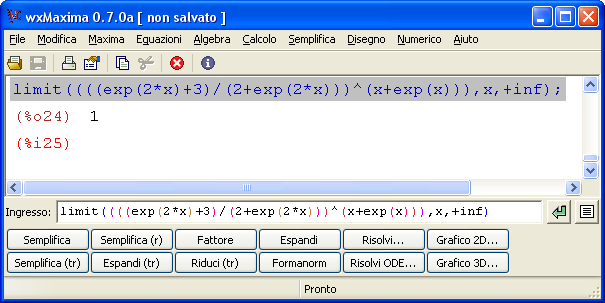
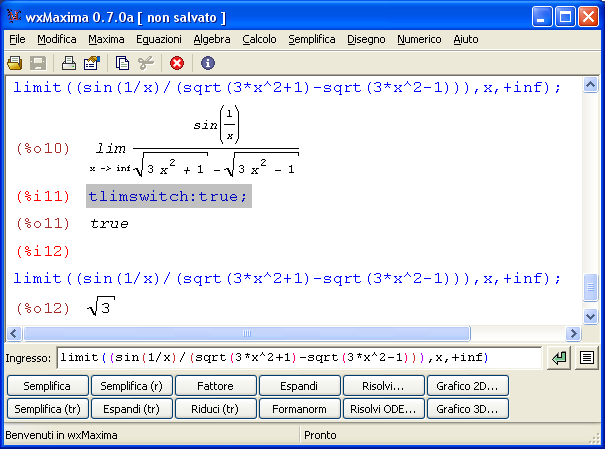
Un test con 30 domande sui limiti notevoli sul calcolo di limiti immediati. Sono gli esercizi sui limiti che è necessario conoscere per risolvere tutti i limiti in matematica.  Maxima è un software gratuito e open source in grado di eseguire calcoli numerici, simbolici, grafici e altre operazioni tipiche della matematica. Fa parte dei software detti CAS (Computer Algebra System) in quanto è in grando non solo di eseguire calcoli matematici passando attraverso le approssimazioni numeriche ma anche e soprattutto di simulare molto bene passaggi e calcoli matematici così come siamo abituati a farlo. In altre parole le risposte che dà il programma non sono approssimazioni numeriche ma risposte ‘esatte’.
Maxima è un software gratuito e open source in grado di eseguire calcoli numerici, simbolici, grafici e altre operazioni tipiche della matematica. Fa parte dei software detti CAS (Computer Algebra System) in quanto è in grando non solo di eseguire calcoli matematici passando attraverso le approssimazioni numeriche ma anche e soprattutto di simulare molto bene passaggi e calcoli matematici così come siamo abituati a farlo. In altre parole le risposte che dà il programma non sono approssimazioni numeriche ma risposte ‘esatte’. 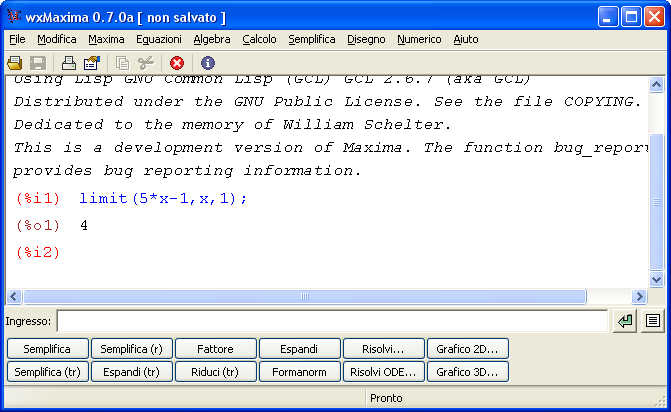
 Il prof. Prinari, docente di matematica al liceo scientifico, mette a disposizione dei colleghi alcuni file Excel realizzati con e per i ragazzi. In questa cartella ha raccolto le formule più ricorrenti nella risoluzione di problemi di geometria analitica sulla retta: tre fogli di lavoro, ognuno dedidicato a uno specifico problema e a una specifica formula.
Il prof. Prinari, docente di matematica al liceo scientifico, mette a disposizione dei colleghi alcuni file Excel realizzati con e per i ragazzi. In questa cartella ha raccolto le formule più ricorrenti nella risoluzione di problemi di geometria analitica sulla retta: tre fogli di lavoro, ognuno dedidicato a uno specifico problema e a una specifica formula.  Nella rete ci sono molti siti belli da vedere, funzionali e ben gestibili, ma purtroppo non ottimizzati per i motori di ricerca. Lo scopo principale di un sito web è quello di farlo trovare dalle persone, altrimenti sarebbe come avere una bella macchina chiusa in garage.
Nella rete ci sono molti siti belli da vedere, funzionali e ben gestibili, ma purtroppo non ottimizzati per i motori di ricerca. Lo scopo principale di un sito web è quello di farlo trovare dalle persone, altrimenti sarebbe come avere una bella macchina chiusa in garage.  Convegno e corso di aggiornamento per docenti di matematica sui temi della nuova didattica per la matematica: giochi, modelli e tecnologie.
Convegno e corso di aggiornamento per docenti di matematica sui temi della nuova didattica per la matematica: giochi, modelli e tecnologie.  Ragazzi, altri 20 quesiti per gli allenamenti ufficiali per la MatematiCup!
Ragazzi, altri 20 quesiti per gli allenamenti ufficiali per la MatematiCup! Esiste un rapporto fecondo che lega la matematica all’origami, l’arte di piegare la carta. Numerosi modelli origami rappresentano oggetti della geometria e viceversa alcune teorie matematiche aiutano a progettare nuovi e particolari modelli. Lucia Gecchelin ha esplorato qualche aspetto di questo legame.
Esiste un rapporto fecondo che lega la matematica all’origami, l’arte di piegare la carta. Numerosi modelli origami rappresentano oggetti della geometria e viceversa alcune teorie matematiche aiutano a progettare nuovi e particolari modelli. Lucia Gecchelin ha esplorato qualche aspetto di questo legame. L’articolo si propone di illustrare, in maniera sintetica e per quanto possibile esaustiva, lo stretto legame tra campi vettoriali, fisica classica ed equazioni differenziali. Fin dall’antichità si pensava che le forze si originassero in seguito ad un contatto, anche ai tempi di Newton, la forza era associata all’idea di spinta o di urto. Tuttavia, quando si intrapresero i primi studi sulla gravitazione universale …
L’articolo si propone di illustrare, in maniera sintetica e per quanto possibile esaustiva, lo stretto legame tra campi vettoriali, fisica classica ed equazioni differenziali. Fin dall’antichità si pensava che le forze si originassero in seguito ad un contatto, anche ai tempi di Newton, la forza era associata all’idea di spinta o di urto. Tuttavia, quando si intrapresero i primi studi sulla gravitazione universale …







 Abbiamo festeggiato da poco l’inizio del nuovo anno, brindando nella notte del 31 dicembre con l’auspicio di un anno il più possibile sereno. Ma dovevamo brindare alle 24.00 oppure alle …
Abbiamo festeggiato da poco l’inizio del nuovo anno, brindando nella notte del 31 dicembre con l’auspicio di un anno il più possibile sereno. Ma dovevamo brindare alle 24.00 oppure alle …


 Euclide immaginato da Justus van Ghent (XV secolo)
Euclide immaginato da Justus van Ghent (XV secolo) 
 Dipinto a olio (96×92), 1923
Dipinto a olio (96×92), 1923