 Una riflessione sulla gestione della scuola da un docente a riposo: decisioni strategiche ribaltate nel momento dell’applicazione, mancanza della cultura dell’organizzazione, controllore e controllato coincidono, … Tante situazioni problematiche messe in evidenza ma anche qualche possibile soluzione: indicare in maniera dettagliata i risultati da conseguire, scomporli e assegnarli ai vari organismi che compongono un sistema complesso come quello scolastico.
Una riflessione sulla gestione della scuola da un docente a riposo: decisioni strategiche ribaltate nel momento dell’applicazione, mancanza della cultura dell’organizzazione, controllore e controllato coincidono, … Tante situazioni problematiche messe in evidenza ma anche qualche possibile soluzione: indicare in maniera dettagliata i risultati da conseguire, scomporli e assegnarli ai vari organismi che compongono un sistema complesso come quello scolastico.
Le decisioni strategiche sempre ribaltate nel momento applicativo
Il legislatore, per affrontare la dinamicità e la complessità della società moderna, ha superato l’obsoleto modello di scuola fondato sulla trasmissione di conoscenza orientando il sistema formativo alla promozione e al potenziamento delle qualità intellettive ed operative dei giovani.
La legge 53/2003 all’art. 2 comma a), ad esempio, afferma la strumentalità di conoscenze e abilità rispetto allo sviluppo di capacità e di competenze. Nel successivo articolo, al comma b), per valutare l’efficacia del servizio, dà mandato all’INVALSI di “effettuare verifiche periodiche e sistematiche sulle conoscenze e abilità degli studenti” istituendo il feedback non sulle finalità ma sugli strumenti.
Un altro esempio è opportuno: i programmi ufficiali degli istituti tecnici commerciali (IGEA e Mercurio), per orientare l’operatività delle scuole, specificano le capacità che devono caratterizzare la figura professionale di quanti concludono il percorso quinquennale. E’ sufficiente prendere visione dei piani dell’offerta formativa elaborati dalle singole scuole per constatare il divario esistente tra la norma e la sua concretizzazione.
La cultura dell’organizzazione è assente
A partire dal 1969 il legislatore ha ridefinito le finalità della scuola per renderle funzionali al contemporaneo contesto socio-culturale. A tal fine è intervenuto sull’assetto organizzativo dando mandato al Consiglio di Circolo/Istituto di “elaborare i criteri generali per la programmazione educativa” [TU 297/94 art. 10/d] indicando, al contempo, funzioni e organi scolastici.
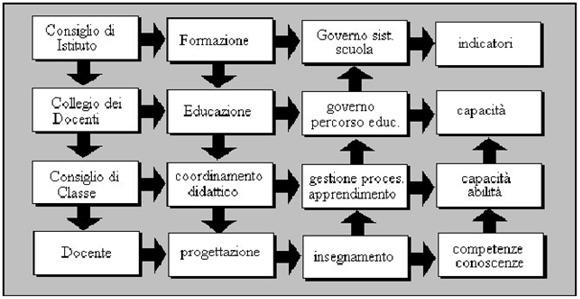
L’adempimento del mandato avrebbe comportato l’introduzione di una terminologia univoca e la specificazione di sicuri riferimenti concettuali e strutturali. Ecco cosa poteva essere fatto:
L’assenza di un sicuro riferimento concettuale ha sterilizzato la legge. Si pensi, ad esempio, al mandato assegnato al collegio dei docenti relativo alla gestione della programmazione educativa, mandato snaturato dal fatto che il termine educazione non viene assunto nel suo significato etimologico ma è, ordinariamente, associato al galateo.
Le figure del controllore e del controllato sono coincidenti
Il Consiglio di Circolo/Istituto ha potere deliberante in materia di “organizzazione e programmazione della vita e dell’attività della scuola” [T.U. 297/94 art. 10/3] e, pertanto, avrebbe potuto disegnare una struttura capitalizzando l’esperienza delle aziende ospedaliere: i dipartimenti disciplinari corrispondono ai reparti delle diverse specialità (i coordinatori dei dipartimenti disciplinari, analogamente ai primari degli ospedali, indirizzano i lavori del gruppo di lavoro per standardizzare protocolli d’insegnamento. L’esercizio della corrispondente libertà trova, nella collegialità, il necessario banco di prova), i consigli di classe all’équipe medica che segue un paziente, la commissione valutazione efficacia del servizio al laboratorio analisi che misura l’evoluzione dello stato di salute dei degenti. Essa opera per monitorare i processi evolutivi delle capacità.
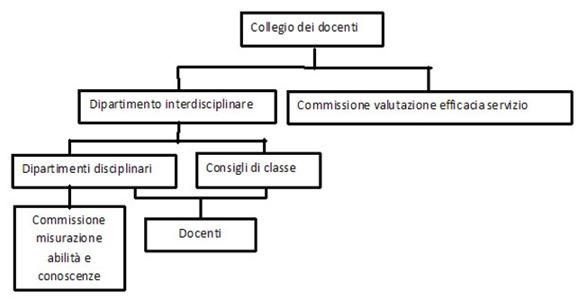
Il dipartimento interdisciplinare, composto dai coordinatori dei due organismi discendenti, potrebbe avere il compito di
Elaborare proposte da sottoporre al collegio riguardanti la programmazione educativa e il coordinamento;
Sanare eventuali contrapposizioni che sorgono tra i due organi discendenti;
Uniformare, nei limiti del possibile, l’attività didattica della scuola;
Produrre resoconti sull’andamento dei lavori, da sottoporre al Collegio dei docenti.
La commissione misurazione abilità e conoscenze è costituita per superare due anomalie presenti nella scuola. La prima riguarda l’ambiguità del rapporto docente-discente: da un lato l’insegnante, per essere incisivo, deve ottenere l’assoluta fiducia dello studente che, senza remore, a lui chiede sostegno, confidandogli difficoltà e mancanze; dall’altro lato il docente è un giudice che raccoglie ogni informazione per formulare oggettive valutazioni. La seconda anomalia riguarda la coincidenza tra controllore e controllato: le valutazioni espresse dal docente sono ordinariamente assunte come parametro dell’efficacia del servizio e, conseguentemente, della validità dell’insegnamento da lui impartito. La normalizzazione si ottiene affidando al professore la valutazione formativa, funzionale al monitoraggio degli apprendimenti; la commissione misurazione abilità e conoscenze sovraintende alla valutazione sommativa, che risolve gli aspetti amministrativi. La struttura organizzativa proposta, inoltre, incide anche sull’efficienza del servizio: più della metà del tempo scuola è ordinariamente assorbito dalle prove scritte e dalle interrogazioni. La commissione valutazione efficacia servizio opera per misurare il grado di maturazione delle capacità degli studenti. La sua operatività è caratterizzata dalla formulazione di quesiti analoghi a quelli in uso nelle Olimpiadi della matematica. Le prove devono proporre situazioni del tutto nuove per gli esaminandi: solo evitando la riproduzione di esperienze pregresse è possibile l’osservazione delle capacità.
L’ordinaria prassi didattica è improduttiva
La ridefinizione della funzione docente come attività progettuale, di ricerca, collegiale è il fondamento dell’ammodernamento della scuola. L’aver posto lo studente a cardine del sistema scolastico attribuisce ai docenti un compito del tutto analogo a quello assegnato a una squadra di operai che realizza un progetto. Il successo del lavoro dipende dall’unitarietà e dal coordinamento dei singoli interventi. Molti sono gli impedimenti a questa riqualificazione. Tra questi risalta per importanza la latitanza degli organismi collegiali che hanno il compito di definire, nel rispetto delle direttive ministeriali, gli obiettivi formativi e gli obiettivi educativi. Il mancato adempimento del mandato conduce a una situazione che mette i docenti in un’insostenibile e mortificante situazione d’indeterminatezza.
La chiave di volta: definire i risultati attesi
L’attività educativa può essere governata solamente se i risultati da conseguire sono dettagliatamente espressi. La complessità del servizio scolastico implica la sua scomposizione in parti e l’assegnazione delle responsabilità relative al conseguimento degli obiettivi a organismi diversi. Il primo raffinamento del problema è operato dal Collegio dei docenti che ha il compito di “curare la programmazione dell’azione educativa”. I momenti salienti di tale attività sono due: la specificazione delle capacità da perseguire e l’indicazione della strategia per il loro conseguimento. Si supponga che sia stato deciso di individuare gli obiettivi prevalenti di ogni anno scolastico: al loro conseguimento sarà orientata, in modo sistematico e intenzionale, l’attività scolatica senza escludere che, a seconda delle circostanze, altri obiettivi possano essere anticipati, ripresi, ampliati e aprofonditi. I traguardi sono espressi in termini di capacità che, come noto, simboleggiano processi: la loro semplice enunciazione non garantisce l’uniformità degli interventi didattici.
Si trascrive uno stralcio del documento di programmazione di un Collegio:
|
Classe
|
Capacità
|
Descrittori di processo
|
|
Prima
|
Applicare modelli
…..
|
Utilizzare efficacemente regole, principi, leggi
Ottenere risultati corretti
|
|
Classe
|
Capacità
|
Descrittori di processo
|
|
Quarta
|
Argomentare/documentare
……
|
Definire l’obiettivo
Formulare ipotesi significative/elencare i dati necessari
Riconoscere/assumere punti di vista differenti
Costruire concatenazioni causa-effetto per pervenire a coerenti conclusioni
Formalizzare il ragionamento
Registrare puntualmente tutte le azioni/decisioni prese nel corso dello sviluppo di un processo
|
Il secondo raffinamento è affidato ai dipartimenti disciplinari che, per ogni anno e per ogni capacità selezionano le conoscenze utili allo sviluppo delle qualità intellettive indicate dal Collegio. L’associazione delle conoscenze alle capacità genera le competenze, gli obiettivi dell’apprendimento. Si trascrive uno stralcio del documento predisposto dal dipartimento di lettere del biennio:
|
DIPARTIMENTO DI LETTERE DEL BIENNIO
Anno di corso: primo
Capacità: applicare modelli
|
|
Conoscenze
|
Competenze
|
Prestazioni osservabili
|
|
I promessi sposi, antologia di testi narrativi(novelle, brani di romanzi, eccc), romanzi
…..
|
Analizzare e interpretare testi utilizzando modelli noti
….
|
Individuare l’organizzazione testuale (sequenze, parole-chiave ecc)
Riconoscere le strutture e le comvenzioni proprie dei diversi tipi di testo
Risalire, attraverso procedure interpretative semplici, dal significato primario al senso indiretto del testo
Definire, in base a precisi riferimenti testuali, la tematica delle letture fatte
|
Il terzo raffinamento compete al dipartimento interdisciplinare e di programmazione che, ricevute le elaborazioni dei dipartimenti disciplinari, ne valuta l’adeguatezza. Le competenze, superato il controllo, vengono tabulate al fine di accertare la reciproca compatibilità. Si trascrive il documento predisposto a tal fine:
|
Classe ….
Tavola sinottica di programmazione: capacità – competenze
Capacità ………….
|
|
Italiano
|
|
|
Storia
|
|
|
Lingua straniera
|
|
|
……
|
|
Il quarto raffinamento è affidato ai consigli di classe che, conoscendo gli studenti, predispongono i piani di intervento. Il quinto raffinamento è a carico dei docenti che progettano e gestiscono occasioni di apprendimento, funzionali ai traguardi da conseguire.
I riferimenti culturali sono inadeguati
La conoscenza è l’elemento caratterizzante la vita della scuola: nel secolo scorso rappresentava il suo fine mentre, nella società contemporanea dinamica e complessa, è lo strumento, l’ambito del lavoro scolastico. Al cambiamento di prospettiva avrebbe dovuto seguire la ricerca del significato di “conoscenza”. In passato esso coincideva con quanto era insegnato nelle università; oggigiorno, vista la sua strumentalità rispetto alla crescita qualitativa dei giovani, il rimanere ancorati a tale assunto appare riduttivo e inidoneo al perseguimento dei traguardi educativi.
E’ pertanto essenziale analizzare le discipline di studio per individuarne i tratti funzionali al raggiungimento delle nuove mete. L’indagine prenderà avvio dallo studio della storia dell’evoluzione delle conoscenze, focalizzerà i problemi che, nel tempo, sono stati affrontati, i procedimenti che sono stati utilizzati per la risoluzione delle questioni poste, la formalizzazione degli argomenti che hanno dato risposta ai quesiti iniziali. Una metafora rappresenta puntualmente tale immagine: le discipline sono dei folletti che saltellano per il mondo e le conoscenze sono le tracce da loro lasciate. Il loro spirito vitale risiede nell’energia, nella curiosità, nella determinazione e nella vivacità del loro carattere. Quale meraviglia manifestano quando percepiscono nuovi problemi, quanta attenzione dimostrano quando ne circoscrivono l’ambito! E che dire della precisione che esibiscono quando scavano per trovare la soluzione e dei trilli di gioia quando catturano nuove questioni.
Il compito dei docenti, pertanto, riguarderà la graduazione di situazioni problematiche da sottoporre agli studenti che, oltre ad acquisire specifiche nozioni, praticheranno i metodi delle diverse discipline. Durante l’attività di ricerca i giovani esibiranno comportamenti strettamente connessi alle capacità messi in gioco, segnali che il docente metterà a frutto per governare i processi di apprendimento.
La progettazione d’itinerari di studio fondata sui problemi e sui metodi non è cosa nuova: una traduzione dal latino, materia la cui potenzialità formativa è universalmente riconosciuta, richiede l’analisi dei dati, la formulazione e l’applicazione di ipotesi, la validazione dei risultati ottenuti.
Il concetto di “qualità” è stato snaturato
La certificazione dell’attività della pubblica amministrazione è stata un’occasione propizia per riportare l’ordinaria gestione scolastica nell’alveo istituzionale.
La certificazione della qualità è la dichiarazione scritta della conformità del servizio a vincoli e a specifici requisiti: nella scuola trova applicazione generalizzata.
La certificazione impegna l’istituzione a prestazioni corrispondenti a standard che garantiscono l’efficacia dei servizi forniti.
La certificazione deve corrispondere alla natura del servizio e, nel caso specifico, alla formazione dei giovani, problema la cui complessità è stata riconosciuta, affrontata e risolta dal legislatore.
La legge individua e specifica le funzioni vitali del sistema e, per ognuna di esse, puntualizza i compiti e individua il soggetto responsabile della relativa soluzione. Per chiarezza di esposizione si richiamano cose precedentemente dette:
* Il rapporto intercorrente tra l’istituto scolastico e la società è curato dal Consiglio di Istituto che ELABORANDO E ADOTTANDO GLI INDIRIZZI GENERALI elenca le capacità e alcune delle competenze che caratterizzeranno gli studenti al termine dell’itinerario formativo. In tal modo la scuola dichiara i caratteri del servizio erogato;
* La programmazione e il controllo dell’efficacia dei processi formativi, rispetto ai traguardi fissati dal Consiglio di Istituto, sono affidati al Collegio dei Docenti;
* L’adeguamento della strategia educativa generale alla peculiarità della singola classe e la scelta delle modalità di convergenza degli insegnamenti verso obiettivi comuni competono al Consiglio di Classe.
I relativi procedimenti attuativi rappresentano l’ossatura portante dell’intero sistema di certificazione di qualità: un’efficace gestione della scuola non può prescindere dell’assunzione di responsabilità degli organismi collegiali. Essi sono chiamati a determinare gli obiettivi, a programmare e controllare i processi educativi.
La certificazione delle relative procedure non consentirebbe alle scuole di sottrarsi alle responsabilità derivanti dalla puntuale applicazione della legge. In particolare non si potrebbe più trascurare il fatto che l’accettazione di un’iscrizione impegna l’istituto scolastico nel suo complesso e che la crescita integrale di uno studente è un problema irrisolvibile per il docente che opera isolatamente.
Nella scuola, invece, la certificazione appare come una formale enunciazione di atti e procedure, secondari rispetto al servizio che deve essere fornito e, conseguentemente, demotiva chi ha l’obbligo di compilare documenti di lampante inutilità.
 Il forum di Teoria dei giochi, moderato da Fioravante Patrone, ordinario di Teoria dei giochi presso l’Università di Genova. Il forum contiene un mini corso di teoria dei giochi, in realtà delle micro lezioni interattive e in forma di dialogo con gli utenti interessati. Ho scritto alcuni post con l’idea che fossero dei "pezzi" di un mini (mini!) corso di TdG.
Il forum di Teoria dei giochi, moderato da Fioravante Patrone, ordinario di Teoria dei giochi presso l’Università di Genova. Il forum contiene un mini corso di teoria dei giochi, in realtà delle micro lezioni interattive e in forma di dialogo con gli utenti interessati. Ho scritto alcuni post con l’idea che fossero dei "pezzi" di un mini (mini!) corso di TdG. 
 Prenome: Licio. Cognome: Gelli. Soprannome: venerabile. Età: anni 89. Professione: risparmiatore tradito. Non è un errore di stampa, anche se per molte vittime del risparmio gestito o della previdenza integrativa sarà una sorpresa trovarsi sulla stessa barca col discusso personaggio, recentemente riapparso in televisione.
Prenome: Licio. Cognome: Gelli. Soprannome: venerabile. Età: anni 89. Professione: risparmiatore tradito. Non è un errore di stampa, anche se per molte vittime del risparmio gestito o della previdenza integrativa sarà una sorpresa trovarsi sulla stessa barca col discusso personaggio, recentemente riapparso in televisione. 


 Simpatico gioco per bambini che vogliono imparare le coordinate cartesiane. Il ranocchio Cartesio deve catturare una mosca che si nasconde tra le ninfee dello stagno, per fortuna lui conosce le coordinate cartesiane. Guida il ranocchio da una ninfea all’altra vicina con il mouse, quando Cartesio raggiunge la foglia giusta fai clic sul fiore di conferma.
Simpatico gioco per bambini che vogliono imparare le coordinate cartesiane. Il ranocchio Cartesio deve catturare una mosca che si nasconde tra le ninfee dello stagno, per fortuna lui conosce le coordinate cartesiane. Guida il ranocchio da una ninfea all’altra vicina con il mouse, quando Cartesio raggiunge la foglia giusta fai clic sul fiore di conferma.  A Pitagora è attribuito il pensiero: "Tutte le cose che si conoscono hanno un numero; senza quello nulla sarebbe possibile conoscere né sapere". Ricordo con molta stima e simpatia un direttore della pianificazione e controllo che aveva una grande fiducia nei numeri del conto economico di un’impresa.
A Pitagora è attribuito il pensiero: "Tutte le cose che si conoscono hanno un numero; senza quello nulla sarebbe possibile conoscere né sapere". Ricordo con molta stima e simpatia un direttore della pianificazione e controllo che aveva una grande fiducia nei numeri del conto economico di un’impresa. 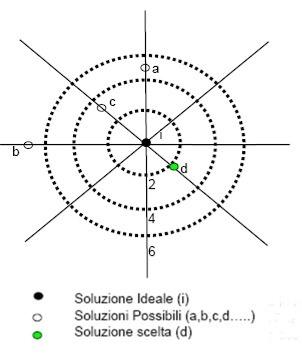

 Tutte le formule di trigonometria che servono in una sola pagina.
Tutte le formule di trigonometria che servono in una sola pagina.  Un eseguibile per generare numeri primi relativamente grandi.
Un eseguibile per generare numeri primi relativamente grandi.  Come influiscono le differenze generazionali e sociali sull’evoluzione della lingua? Come è possibile trasferire il sapere tra sistemi e culture diverse? Quale impatto hanno sulla vita quotidiana le espressioni dei media e della pubblicità? In che modo la tecnologia modifica i processi di comunicazione e come l’uomo si rapporta con il mondo?
Come influiscono le differenze generazionali e sociali sull’evoluzione della lingua? Come è possibile trasferire il sapere tra sistemi e culture diverse? Quale impatto hanno sulla vita quotidiana le espressioni dei media e della pubblicità? In che modo la tecnologia modifica i processi di comunicazione e come l’uomo si rapporta con il mondo?  Sono ancora disponibili alcune borse di studio per partecipare al Diploma On Line per Esperti di didattica assistita dalle Nuove Tecnologie del Politecnico di Milano. Le borse di studio, frutto di una ormai consolidata collaborazioni con gli Uffici Scolastici di 15 Regioni italiane, possono essere richieste direttamente dal sito del corso. La scadenza ultima per presentare la propria candidatura è venerdì 31 ottobre 2008.
Sono ancora disponibili alcune borse di studio per partecipare al Diploma On Line per Esperti di didattica assistita dalle Nuove Tecnologie del Politecnico di Milano. Le borse di studio, frutto di una ormai consolidata collaborazioni con gli Uffici Scolastici di 15 Regioni italiane, possono essere richieste direttamente dal sito del corso. La scadenza ultima per presentare la propria candidatura è venerdì 31 ottobre 2008.  … ma insegnagli a pescare.
… ma insegnagli a pescare. 
 Gioca alle tabelline con Robin Hood, scegli la freccia giusta e colpisci il bersaglio.
Gioca alle tabelline con Robin Hood, scegli la freccia giusta e colpisci il bersaglio. In questi giorni è di attualità affrontare il problema della crisi finanziaria che sta investendo, a più riprese, l’economia mondiale. Il piano Paulson è solo uno dei tanti metodi adottati in questi giorni, per il salvataggio del sistema finanziario. Visita il forum di teoria dei giochi.
In questi giorni è di attualità affrontare il problema della crisi finanziaria che sta investendo, a più riprese, l’economia mondiale. Il piano Paulson è solo uno dei tanti metodi adottati in questi giorni, per il salvataggio del sistema finanziario. Visita il forum di teoria dei giochi.  Una riflessione sulla gestione della scuola da un docente a riposo: decisioni strategiche ribaltate nel momento dell’applicazione, mancanza della cultura dell’organizzazione, controllore e controllato coincidono, … Tante situazioni problematiche messe in evidenza ma anche qualche possibile soluzione: indicare in maniera dettagliata i risultati da conseguire, scomporli e assegnarli ai vari organismi che compongono un sistema complesso come quello scolastico.
Una riflessione sulla gestione della scuola da un docente a riposo: decisioni strategiche ribaltate nel momento dell’applicazione, mancanza della cultura dell’organizzazione, controllore e controllato coincidono, … Tante situazioni problematiche messe in evidenza ma anche qualche possibile soluzione: indicare in maniera dettagliata i risultati da conseguire, scomporli e assegnarli ai vari organismi che compongono un sistema complesso come quello scolastico. 

 Formulario: tutto sulle progressioni numeriche, definizioni proprietà, formule ed esempi.
Formulario: tutto sulle progressioni numeriche, definizioni proprietà, formule ed esempi.  Il paragrafo 10 del formulario completo di matematica: sistemi di numerazione – sistema decimale – sistema binario – sistema esadecimale – sistema di numerazione romano.
Il paragrafo 10 del formulario completo di matematica: sistemi di numerazione – sistema decimale – sistema binario – sistema esadecimale – sistema di numerazione romano.  Uno dei modi più semplici per scrivere i numeri è fare delle tacche sulla carta, o su un bastone, o per terra, a seconda di cosa si ha a disposizione. In effetti molte volte torna comodo, tranne se si devono scrivere numeri grandi. E quante tacche ci vorranno se si volesse scrivere una intera enciclopedia. Paradossalmente basta una sola tacca. Come?
Uno dei modi più semplici per scrivere i numeri è fare delle tacche sulla carta, o su un bastone, o per terra, a seconda di cosa si ha a disposizione. In effetti molte volte torna comodo, tranne se si devono scrivere numeri grandi. E quante tacche ci vorranno se si volesse scrivere una intera enciclopedia. Paradossalmente basta una sola tacca. Come? 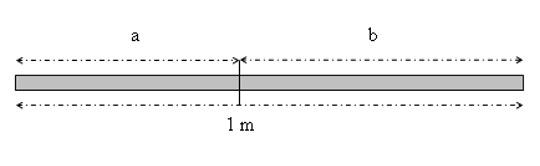
 Lao-tzu, fondatore del taoismo e contemporaneo di Confucio (VI-V sec. A.C.) sebbene di qualche decina di anni più vecchio, sosteneva che, se un governo vuole attenersi al tao, deve ridurre al minimo l’ingerenza della politica nella vita dei suoi sudditi (posizione che oggi sarebbe condivisa da molti liberisti) e lasciare che la natura segua il suo corso.
Lao-tzu, fondatore del taoismo e contemporaneo di Confucio (VI-V sec. A.C.) sebbene di qualche decina di anni più vecchio, sosteneva che, se un governo vuole attenersi al tao, deve ridurre al minimo l’ingerenza della politica nella vita dei suoi sudditi (posizione che oggi sarebbe condivisa da molti liberisti) e lasciare che la natura segua il suo corso.  Lao-tzu, fondatore del taoismo e contemporaneo di Confucio (VI-V sec. A.C.) sebbene di qualche decina di anni più vecchio, sosteneva che, se un governo vuole attenersi al tao, deve ridurre al minimo l’ingerenza della politica nella vita dei suoi sudditi (posizione che oggi sarebbe condivisa da molti liberisti) e lasciare che la natura segua il suo corso.
Lao-tzu, fondatore del taoismo e contemporaneo di Confucio (VI-V sec. A.C.) sebbene di qualche decina di anni più vecchio, sosteneva che, se un governo vuole attenersi al tao, deve ridurre al minimo l’ingerenza della politica nella vita dei suoi sudditi (posizione che oggi sarebbe condivisa da molti liberisti) e lasciare che la natura segua il suo corso.  Gioca ai nostri sudoku on line, numerosi sudoku da stampare, sudoku da scaricare. Sudoku per ogni livello, facilissimi per bamabini, con l’uso di poche lettere, fino a sudoku con 16 simboli per veri esperti. Inoltre una guida per imparare a risolvere il gioco. Vai alla nostra sezione sul
Gioca ai nostri sudoku on line, numerosi sudoku da stampare, sudoku da scaricare. Sudoku per ogni livello, facilissimi per bamabini, con l’uso di poche lettere, fino a sudoku con 16 simboli per veri esperti. Inoltre una guida per imparare a risolvere il gioco. Vai alla nostra sezione sul  Numeri al posto di lettere: conosci la provincia di Potenza?
Numeri al posto di lettere: conosci la provincia di Potenza?  Il dibattito sul ruolo della scuola, le sue finalità, i suoi strumenti, il suo costo in termini economici e sociali, diviene di anno in anno sempre più acceso, in vista anche di importanti decisioni, spesso di natura esclusivamente economica, che la società attuale è obbligata a prendere. La recente valutazione della scuola, in termini di sostenibilità del modello economico che la sorregge, sembra affermare che la scuola ha un costo insostenibile; un lusso che la società attuale in piena crisi economica è costretta a ridimensionare. Ripropongo su questo tema alcune riflessioni fatte da Lucio Russo in un libro edito per la prima volta nel 1998 e ripubblicato con qualche aggiornamento nel 2005.
Il dibattito sul ruolo della scuola, le sue finalità, i suoi strumenti, il suo costo in termini economici e sociali, diviene di anno in anno sempre più acceso, in vista anche di importanti decisioni, spesso di natura esclusivamente economica, che la società attuale è obbligata a prendere. La recente valutazione della scuola, in termini di sostenibilità del modello economico che la sorregge, sembra affermare che la scuola ha un costo insostenibile; un lusso che la società attuale in piena crisi economica è costretta a ridimensionare. Ripropongo su questo tema alcune riflessioni fatte da Lucio Russo in un libro edito per la prima volta nel 1998 e ripubblicato con qualche aggiornamento nel 2005. 
 Per Talete, vissuto attorno al 600 a.C., il principio di tutte le cose era l’acqua. Oggi gli scienziati ci dicono che per sapere se su un pianeta (ad esempio Marte) è possibile trovare tracce di vita la precondizione è scoprire se su di esso ci sia, o ci sia stata, l’acqua. Sempre oggi molti scienziati e futurologi ci spiegano che il principale problema dell’organizzazione planetaria sarà in futuro, forse ancor prima del cibo e dell’energia, quello dell’accesso all’acqua per tutte le popolazioni.
Per Talete, vissuto attorno al 600 a.C., il principio di tutte le cose era l’acqua. Oggi gli scienziati ci dicono che per sapere se su un pianeta (ad esempio Marte) è possibile trovare tracce di vita la precondizione è scoprire se su di esso ci sia, o ci sia stata, l’acqua. Sempre oggi molti scienziati e futurologi ci spiegano che il principale problema dell’organizzazione planetaria sarà in futuro, forse ancor prima del cibo e dell’energia, quello dell’accesso all’acqua per tutte le popolazioni.  Obiettivo del Master è quello di portare, con un percorso formativo biennale accessibile come tempi e modalità anche a chi già lavora, a una conoscenza approfondita e operativa del mondo dell’e-learning e dei suoi strumenti e metodi più avanzati. Le iscrizioni sono aperte fino al 15 novembre.
Obiettivo del Master è quello di portare, con un percorso formativo biennale accessibile come tempi e modalità anche a chi già lavora, a una conoscenza approfondita e operativa del mondo dell’e-learning e dei suoi strumenti e metodi più avanzati. Le iscrizioni sono aperte fino al 15 novembre.  Un test per capire che tipo sei. Attento al trucco … anzi alla matemagica!
Un test per capire che tipo sei. Attento al trucco … anzi alla matemagica! 
 La Bibbia raccontà che Mosè, mentre guidava il suo popolo dall’ Egitto alla Terra promessa, stabilisse, con l’aiuto di Dio, le regole fondamentali per l’organizzazione e la convivenza civile (circa 1250 a.C.). I problemi che doveva affrontare e che il popolo quotidianamente gli sottoponeva erano i più vari: lavoro, agricultura, bestiame, casa, cibo, legna, produzione di manufatti, costruzioni, acquisti, scribi, banche, giustizia, tasse, scuola, religione, diritto di famiglia, sanità, servitori, addestramento militare, difesa, ecc.
La Bibbia raccontà che Mosè, mentre guidava il suo popolo dall’ Egitto alla Terra promessa, stabilisse, con l’aiuto di Dio, le regole fondamentali per l’organizzazione e la convivenza civile (circa 1250 a.C.). I problemi che doveva affrontare e che il popolo quotidianamente gli sottoponeva erano i più vari: lavoro, agricultura, bestiame, casa, cibo, legna, produzione di manufatti, costruzioni, acquisti, scribi, banche, giustizia, tasse, scuola, religione, diritto di famiglia, sanità, servitori, addestramento militare, difesa, ecc.  Un giorno Ietro, il suocero di Mosé, lo vide che come di consueto stava al centro del suo popolo per ascoltare, comprendere e risolvere i problemi di tutti.
Un giorno Ietro, il suocero di Mosé, lo vide che come di consueto stava al centro del suo popolo per ascoltare, comprendere e risolvere i problemi di tutti. 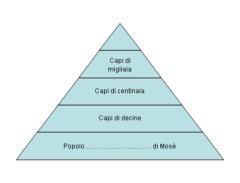
 Questo fascicolo presenta Animat (Associazione Nazionale Insegnanti di Matematica), ciò che è e ciò che intende essere. Presenta quindi ciò che si anima in essa, ricostruito in primo luogo attraverso il dibattito in rete, nel corso dell’anno scolastico 2007-2008, nella lista Fondanimat. Presenta le voci, le riflessioni e l’impegno di chi insegna matematica, dalla primaria in su, la vuole insegnare meglio, vuole stare meglio e vuole contribuire, anche attraverso il suo lavoro, al miglioramento dell’insegnamento della matematica e della qualità della scuola italiana.
Questo fascicolo presenta Animat (Associazione Nazionale Insegnanti di Matematica), ciò che è e ciò che intende essere. Presenta quindi ciò che si anima in essa, ricostruito in primo luogo attraverso il dibattito in rete, nel corso dell’anno scolastico 2007-2008, nella lista Fondanimat. Presenta le voci, le riflessioni e l’impegno di chi insegna matematica, dalla primaria in su, la vuole insegnare meglio, vuole stare meglio e vuole contribuire, anche attraverso il suo lavoro, al miglioramento dell’insegnamento della matematica e della qualità della scuola italiana.  In questo articolo, dopo aver tracciato una brevissima storia sulle dimostrazioni proposte nel corso dei secoli circa l’infinità dei numeri primi, viene proposta una dimostrazione alternativa del professor Aldo Scimone, apparsa nella rivista Teaching Mathematics and its Applications Advance Access.
In questo articolo, dopo aver tracciato una brevissima storia sulle dimostrazioni proposte nel corso dei secoli circa l’infinità dei numeri primi, viene proposta una dimostrazione alternativa del professor Aldo Scimone, apparsa nella rivista Teaching Mathematics and its Applications Advance Access. Fresco di stampa il libro di Walter Maraschini "Bravi in matematica", edito da Bruno Mondadori.
Fresco di stampa il libro di Walter Maraschini "Bravi in matematica", edito da Bruno Mondadori.  Il messaggero aveva la lingua pesante … . Il signore di Uruk impastò l’argilla e vi incise le parole come in una tavoletta; prima nessuno aveva mai inciso parole nell’argilla.
Il messaggero aveva la lingua pesante … . Il signore di Uruk impastò l’argilla e vi incise le parole come in una tavoletta; prima nessuno aveva mai inciso parole nell’argilla.  I cacciatori-raccoglitori del paleolitico e poi del mesolitico (15.000-8.000) a.C. usavano tacche incise su punteruoli d’osso per contare con un sistema di corrispondenza univoca.
I cacciatori-raccoglitori del paleolitico e poi del mesolitico (15.000-8.000) a.C. usavano tacche incise su punteruoli d’osso per contare con un sistema di corrispondenza univoca.  Un cruciverba per matematici
Un cruciverba per matematici  Si può raccontare la storia della matematica, come si può raccontare la storia dei matematici. Alcuni preferiscono la prima, ed ecco che la matematica si presenta come un continuum che si evolve nel tempo, una progressiva acquisizione di conoscenza.
Si può raccontare la storia della matematica, come si può raccontare la storia dei matematici. Alcuni preferiscono la prima, ed ecco che la matematica si presenta come un continuum che si evolve nel tempo, una progressiva acquisizione di conoscenza.  A distanza di trent’anni Bollati Boringhieri ripubblica un libro fondamentale per la didattica della logica e della matematica in generale. Come osserva Corrado Mangione (professore di Storia della logica presso l’Università di Milano) nella prefazione a questa nuova edizione, quando il libro venne pubblicato per la prima volta in Italia nel 1973 l’insegnamento della logica era del tutto assente nella scuola primaria e secondaria italiana. Cominciava ad ‘attecchire’ nelle università e ciò creava una frattura tra l’insegnamento nella scuola superiore e quello nell’università.
A distanza di trent’anni Bollati Boringhieri ripubblica un libro fondamentale per la didattica della logica e della matematica in generale. Come osserva Corrado Mangione (professore di Storia della logica presso l’Università di Milano) nella prefazione a questa nuova edizione, quando il libro venne pubblicato per la prima volta in Italia nel 1973 l’insegnamento della logica era del tutto assente nella scuola primaria e secondaria italiana. Cominciava ad ‘attecchire’ nelle università e ciò creava una frattura tra l’insegnamento nella scuola superiore e quello nell’università.  Enrico Giusti è un noto studioso di Analisi matematica, ha ottenuto nel 1968 il premio Pomini e nel 1978 il premio Caccioppoli. Nel 1999 ha ricevuto la medaglia dell’Accademia Nazionale delle Scienze detta dei XL per i suoi studi in Matematica e in Storia della Matematica. I suoi interessi scientifici hanno riguardato prima le equazioni alle derivate parziali e il calcolo delle variazioni, poi la storia della matematica e più di recente la divulgazione della matematica. Ricordiamo il libro del 2004 "La matematica in cucina", edito da Bollati Boringheri. Nel 1999 ha fondato “Il Giardino di Archimede” (http://web.math.unifi.it/archimede/archimede) , il primo museo dedicato completamente alla matematica.
Enrico Giusti è un noto studioso di Analisi matematica, ha ottenuto nel 1968 il premio Pomini e nel 1978 il premio Caccioppoli. Nel 1999 ha ricevuto la medaglia dell’Accademia Nazionale delle Scienze detta dei XL per i suoi studi in Matematica e in Storia della Matematica. I suoi interessi scientifici hanno riguardato prima le equazioni alle derivate parziali e il calcolo delle variazioni, poi la storia della matematica e più di recente la divulgazione della matematica. Ricordiamo il libro del 2004 "La matematica in cucina", edito da Bollati Boringheri. Nel 1999 ha fondato “Il Giardino di Archimede” (http://web.math.unifi.it/archimede/archimede) , il primo museo dedicato completamente alla matematica.  L’intersezione tra matematici e letterati si sa è pressoché nulla. In questa raccolta antologica sono presenti 21 racconti di altrettanti autori: matematici, fisici, filosofi, storici, medici.
L’intersezione tra matematici e letterati si sa è pressoché nulla. In questa raccolta antologica sono presenti 21 racconti di altrettanti autori: matematici, fisici, filosofi, storici, medici.  Il libro raccoglie i testi di un ciclo di conferenze organizzato dagli Amici dell’Acquario, in collaborazione con l’Acquario stesso e con il "Colloquium Mathematicum" del Dipartimento di Matematica dell’Università di Genova.
Il libro raccoglie i testi di un ciclo di conferenze organizzato dagli Amici dell’Acquario, in collaborazione con l’Acquario stesso e con il "Colloquium Mathematicum" del Dipartimento di Matematica dell’Università di Genova.  Com’è fatto l’universo in cui viviamo? Da secoli scienziati e filosofi cercano di rispondere a questa domanda, fornendo risposte sempre nuove e inaspettate. Le più recenti teorie fisiche arrivano addirittura a ipotizzare che il nostro universo abbia ben undici dimensioni (più quella temporale) e che i costituenti ultimi della materia che ci circonda siano delle minuscole stringhe chiuse che vibrano ad una velocità inimmaginabile.
Com’è fatto l’universo in cui viviamo? Da secoli scienziati e filosofi cercano di rispondere a questa domanda, fornendo risposte sempre nuove e inaspettate. Le più recenti teorie fisiche arrivano addirittura a ipotizzare che il nostro universo abbia ben undici dimensioni (più quella temporale) e che i costituenti ultimi della materia che ci circonda siano delle minuscole stringhe chiuse che vibrano ad una velocità inimmaginabile.  Mettere da parte un gruzzoletto di soldi non è cosa facile, oggi ancora meno di qualche anno fa. Su quei bigliettini di carta, spesso semplicemente bit di computer presso le banche, ognuno ci fa i suoi sogni, la sua tranquillità: la macchina, la vacanza, l’università per i figli, la sicurezza "perché non si può mai sapere!". Mettere da parte i soldi è un’impresa difficile, ma cercare di non farseli ‘fregare’ è ancora più difficile. I sogni che noi facciamo sui nostri soldi, purtroppo, li fanno anche gli altri, sempre sui nostri soldi. I ladri? gli scippatori? i truffatori? le associazioni criminali? l’inflazione? Non solo. Beppe Scienza svela, per chi non se ne fosse ancora accorto, un mondo di veri e propri truffatori mascherati da consulenti finanziari e, purtroppo, accreditati giornalisti economici di ancor più accreditate testate giornalistiche.
Mettere da parte un gruzzoletto di soldi non è cosa facile, oggi ancora meno di qualche anno fa. Su quei bigliettini di carta, spesso semplicemente bit di computer presso le banche, ognuno ci fa i suoi sogni, la sua tranquillità: la macchina, la vacanza, l’università per i figli, la sicurezza "perché non si può mai sapere!". Mettere da parte i soldi è un’impresa difficile, ma cercare di non farseli ‘fregare’ è ancora più difficile. I sogni che noi facciamo sui nostri soldi, purtroppo, li fanno anche gli altri, sempre sui nostri soldi. I ladri? gli scippatori? i truffatori? le associazioni criminali? l’inflazione? Non solo. Beppe Scienza svela, per chi non se ne fosse ancora accorto, un mondo di veri e propri truffatori mascherati da consulenti finanziari e, purtroppo, accreditati giornalisti economici di ancor più accreditate testate giornalistiche.  A dieci anni dalla morte di Ennio De Giorgi, il Dipartimento di Matematica dell’Università del Salento, ha organizzato un seminario per ricordare il ruolo scientifico e umano del noto matematico salentino che ha contribuito in maniera decisiva alla nascita della Facoltà di Scienze a Lecce. Gli atti del seminario sono stati raccolti e curati in un volume da Diego Pallara e Mario Spedicato.
A dieci anni dalla morte di Ennio De Giorgi, il Dipartimento di Matematica dell’Università del Salento, ha organizzato un seminario per ricordare il ruolo scientifico e umano del noto matematico salentino che ha contribuito in maniera decisiva alla nascita della Facoltà di Scienze a Lecce. Gli atti del seminario sono stati raccolti e curati in un volume da Diego Pallara e Mario Spedicato.