Il software Cabri géomètre è stato sviluppato da Y. Baulac, F. Bellemain e J. M. La Borde presso l’Università di Grenoble (la prima versione del software risale al 1988, la versione più recente è la Cabri II plus del 2003) come supporto all’insegnamento della geometria euclidea. Nelle ultime versioni è stato implementato l’uso delle coordinate cartesiane per integrare l’approccio sintetico con quello analitico.
Il programma utilizza lo schermo del computer come un foglio di disegno, ha una barra di strumenti tipici della geometria euclidea e del disegno su carta: punti, rette, segmenti, poligoni, compasso, misure di segmenti, di angoli, di aree, … Questi strumenti permettono di disegnare sul monitor in modo abbastanza simile a come si disegna su carta con matita, riga e compasso.
Non si tratta di una simulazione come finzione, ma di un uso concettuale degli strumenti elementari: per disegnare una retta l’allievo deve indicare un punto, gli compare una retta mobile ma vincolata al punto, l’allievo ‘vede’ un fascio di rette e ha un’idea immediata di un concetto abbastanza complesso da intuire, quindi deve indicare un secondo punto per fissare la retta, si rende conto che due punti individuano una retta; per disegnare una circonferenza l’allievo indica prima il centro e poi il raggio; e così via.
L’idea innovativa del software, che è ciò che lo rende particolarmente interessante a fini didattici, è la possibilità di agire sulla figura costruita muovendo, con il trascinamento del mouse, i punti ‘liberi’ della costruzione: l’allievo può osservare ciò che resta inalterato e ciò che varia. Rispetto al disegno su carta lo studente si rende conto delle relazioni tra gli enti geometrici realizzati: appartenenza di un punto a una retta, perpendicolarità o parallelismo tra rette, ecc.
Interfaccia utente
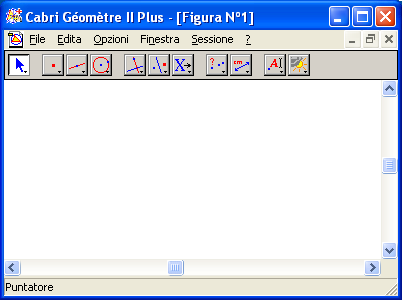
Barra dei menu:
File contiene i principali comandi per l’uso dei file (aprire, chiudere, salvare, stampare) ma anche la possibilità di visualizzare l’intera area di disegno.
Edita permette anche di ripetere passo passo la costruzione geometrica.
Opzioni permette di personalizzare la finestra di lavoro.
Finestra permette di agire sulla finestra di lavoro e modificarne le impostazioni.
Sessione permette di registrare la sessione di lavoro.
Barra degli strumenti:

Puntatore: permette di modificare gli oggetti disegnati trascinando alcuni o tutti gli elementi della costruzione.
Punto: per disegnare un punto che può essere libero, può essere vincolato a restare su un luogo geometrico, può essere il punto di intersezione di due luoghi geometrici.
Retta: permette di disegnare elementi rettilinei: rette, semirette, segmenti, vettori, triangoli, poligoni e poligoni regolari.
Circonferenza: permette di disegnare circonferenze, archi di circonferenze e coniche.
Costruzioni: permette di disegnare elementi ottenuti da costruzioni geometriche: retta perpendicolare a una retta data, retta parallela, punto medio, asse, bisettrice, luoghi,…
Trasformazioni: permette di applicare trasformazioni geometriche di base: simmetria assiale, simmetria centrale, traslazione, rotazione, omotetia, inversione.
Macro: per realizzare nuove costruzioni di base da poter utilizzare semplicemente richiamandole.
Verifica: per verificare se gli elementi della costruzione soddisfano alcune proprietà come l’allineamento di punti, il parallelismo e la perpendicolarità di rette, l’equidistanza e l’appartenenza.
Misura: per effettuare misure sugli oggetti geometrici della costruzione: lunghezze, aree, inclinazioni, angoli, coordinate, …
Visualizza: permette di contrassegnare gli elementi della costruzione: assegnare nomi, aggiungere del testo esplicativo, segnare un angolo; permette anche di animare la costruzione.
Disegna: contiene i principali strumenti per personalizzare il disegno: mostrare o nascondere alcuni elementi della costruzione, per esempio i passaggi intermedi, aggiungere il bottone mostra/nascondi, modificare i colori e il tratteggio del disegno; mostrare gli assi cartesiani.
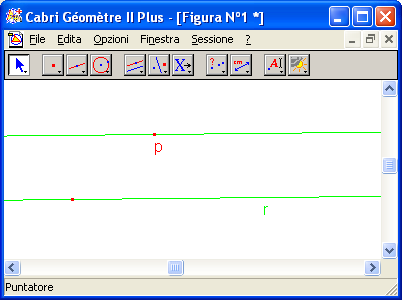
Esempio 1
Per un punto esterno a una retta disegnare la parallela alla retta e passante per il punto dato.
1. Disegnare la retta con lo strumento Retta.
2. Assegnare il nome r alla retta con lo strumento Visualizza.
3. Disegnare un punto esterno alla retta con lo strumento Punto.
4. Assegnare il nome al punto con lo strumento Visualizza.
5. Attivare dallo strumento Costruzioni lo strumento Retta parallela, indicare con il puntatore la retta r e poi il punto P.
Esempio 2
Costruire la retta di Eulero di un triangolo. Questo disegno è praticamente impossibile da realizzare non solo sulla lavagna ma anche su carta con riga e squadrette.
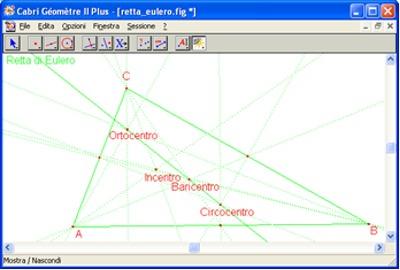
Cabri, quindi può essere utilizzato come una lavagna di precisione, con elevato grado di leggibilità dei disegni.
Quando e come usarlo a scuola
Il software non vincola a percorsi didattici prefissati, può essere utilizzato liberamente per trattare quasi tutti gli argomenti della geometria elementare e può anche essere usato semplicemente come lavagna luminosa.
Scuola primaria: disegno di punti, rette, poligoni, circonferenze, lunghezze e aree
Scuola secondaria di 1° grado: tutti gli argomenti di geometria piana, incluse le trasformazioni geometriche
Scuola secondaria di 2° grado: tutti gli argomenti di geometria sintetica del biennio, geometria analitica, rappresenta di funzioni e di luoghi geometrici nel triennio.
Costi e licenze
Produttore: Cabri Geometry II è un marchio registrato presso l’Universitè Joseph Fourier di Grenoble (Francia) Distributore: Texas Instruments Distributore italiano: Campustore Siti di riferimento:
www.campustore.it;
http://education.ti.com/us/product/software.html
Licenze: commerciale; la versione Demo è scaricabile liberamente ma non ha abilitata la funzione di salvare le costruzioni
Lingua: In diverse lingue, anche in italiano.
Requisiti tecnici: Esiste la versione per Windows e quella per Macintosh
Manuali e guide: Cabri Manuale, http://education.ti.com/downloads/guidebooks/it/gbbook_ita.pdf
Per altri manuali didattici consulta la bibliografia.
La guida in linea del programma è attivabile dal tasto F1, nella parte inferiore della finestra di lavoro compare il suggerimento relativo allo strumento che si deve usare.
Estensione dei file prodotti e supportati
Le costruzioni possono essere salvate, i file hanno estensione .fig e grandezza introno ai 5 KB.
E’ possibile anche salvare delle Macro, ossia delle costruzioni di base che possono essere richiamate nella costruzione di una figura più complessa. Per esempio, è possibile salvare una Macro che disegni un quadrato di lato assegnato e richiamare la macro nelle costruzioni che fanno uso di uno o più quadrati. L’estensione dei file macro è .mac, la dimensione di questo file è di 1KB o poco più.
E’ possibile produrre Applet Java, ma solo con la versione precedente del programma, la Cabri II.
Bibliografia
Green D., 1994, Cabri-géomètre, la rivincita di Euclide, Quaderni CabrIRRSAE (n. 1), a cura dell’IRRE Emilia Romagna.
L’autore mette in evidenza le motivazioni che hanno portato alla realizzazione del software Cabri e gli usi didattici, l’articolo fa riferimento a una delle prime versioni di Cabri, ma è utile per capire lo spirito del programma. “Il grido dei moderni movimenti matematici agli inizi degli anni ’60 era "Abbasso Euclide!" Un software di pregio chiamato Cabri-géomètre potrebbe invertire l’abbandono della geometria euclidea nelle scuole”.
CabriIRRSAE, 1994, Intervista a C. Laborde, CabrIRRSAE (n. 1, 1994), a cura dell’IRRE Emilia Romagna.
Intervista a Colette La Borde un membro dell’equipe che ha realizzato Cabri Géomètre
Paola D., 2004, “Software di geometria dinamica per un sensato approccio alla dimostrazione in geometria: un esempio di Laboratorio di Matematica”, in Progetto Alice (13), Pagine, Roma, pp. 103-121.
L’autore propone un’esperienza di laboratorio con l’uso di Cabri centrata sul valore didattico della dimostrazione in geometria. Il sensato approccio si riferisce ai sensi e quindi all’esperienza e alla percezione.
Boieri P., Dané C. , 2003, Geometria con Cabri, costruire, scoprire dimostrare, Loescher, Torino.
Manuale di geometria per la scuola secondaria di 2° grado che fanno uso di Cabri
R. Sabbadini, Fisicabri, Principato, Milano, 2005.
Simulazioni di argomenti di fisica (meccanica, termodinamica, onde e ottica, relatività, elettromagnetismo) ed esercizi di fisica con Cabri
AA. VV., Sperimentazione di didattica della matematica con Cabri, nella Scuola Media Statale Don Milani, Venaria Reale (TO)
https://www.matematicamente.it//didattica/percorsi_didattici/sperimentazione_di_didattica_della_matematica_con_cabri_200711302393/ Un percorso didattico sull’insegnamento della geometria con Cabri, completo di schede ed esercizi per gli studenti della scuola secondaria di 1° grado. Il percorso presentato è stato effettivamente realizzato in classe.
Di Stefano C., 2005, “Le trasformazioni geometriche e Cabri”, in Progetto Alice (16), Pagine, Roma, pp. 27-42.
L’autore presenta semplici attività da svolgere con Cabri su uno dei temi che maggiormente in risalto le potenzialità di questo software.
Cabrinews, http://www.fardiconto.it/cabrinews/
Lista di discussione frequentata principalmente da insegnati che condividono dubbi e proposte sull’uso di Cabri ma anche sui temi dell’insegnamento della matematica.
CabriIRRSAE, http://www.fardiconto.it/cabrirrsae/
Bollettino e Quaderni pubblicati on line e di libera consultazione. La pubblicazione tuttavia è ferma per mancanza di fondi al n.39 di Aprile 2004.
CabriJava, http://kidslink.scuole.bo.it/fardiconto/cabrijava/
Sito per le Applet Java che si possono ottenere con Cabri. E’ possibile scaricare gratuitamente i componenti aggiuntivi per produrre le Applet, trovare indicazioni per la produzione di Applet, esempi.
Autore della scheda: Antonio Bernardo
Anno: 2005
 Convegno-simposio su "L’insegnamento della matematica con i nuovi software: esperienze e risultati in onore di Pico Fonticulano" 30 aprile, 1-2-3 maggio 2009, Fontecchio (AQ).
Convegno-simposio su "L’insegnamento della matematica con i nuovi software: esperienze e risultati in onore di Pico Fonticulano" 30 aprile, 1-2-3 maggio 2009, Fontecchio (AQ). 
 Si farà uso delle abilità acquisite sul concetto di equiscomponibilità per verificare i Teroremi di Euclide e il Teorema di Pitagora in modo che gli allievi ne arrivino a capire gli enunciati più chiaramente. Completeremo il discorso sull’equiscomponibilità verificando che, grazie ai teoremi di Euclide, è possibile costruire un quadrato che ha la stessa area di un rettangolo dato. Questa tesi partecipa al concorso Condividi la tua tesi e vinci tre Apple iPhone 3G
Si farà uso delle abilità acquisite sul concetto di equiscomponibilità per verificare i Teroremi di Euclide e il Teorema di Pitagora in modo che gli allievi ne arrivino a capire gli enunciati più chiaramente. Completeremo il discorso sull’equiscomponibilità verificando che, grazie ai teoremi di Euclide, è possibile costruire un quadrato che ha la stessa area di un rettangolo dato. Questa tesi partecipa al concorso Condividi la tua tesi e vinci tre Apple iPhone 3G  A volte per risolvere un problema occorre analizzarlo fin nei più minimi dettagli, quindi dimenticare tutto e ripensare dall’inizio liberi dai pregiudizi. Un “matto in due (mosse)” è un problema di questo tipo: viene proposta una posizione, e il colore che deve giocare (di solito per semplicità è il bianco) deve effettuare una mossa tale che dopo una qualunque risposta dell’altro colore, si possa dare scacco matto in una mossa.
A volte per risolvere un problema occorre analizzarlo fin nei più minimi dettagli, quindi dimenticare tutto e ripensare dall’inizio liberi dai pregiudizi. Un “matto in due (mosse)” è un problema di questo tipo: viene proposta una posizione, e il colore che deve giocare (di solito per semplicità è il bianco) deve effettuare una mossa tale che dopo una qualunque risposta dell’altro colore, si possa dare scacco matto in una mossa.  Questo tipo di problema differisce dai problemi del tipo “il bianco muove e vince”, dato che qui lo scopo non è vincere ma dare matto nel numero di mosse prefissato. Consideriamo per esempio la posizione del diagramma (autore: Yochanan Afek). La consegna è: “il bianco muove e matta in due mosse”. Osserviamo senza troppa fatica che non si può dare matto in una sola mossa. Ed osserviamo anche che, come sempre nei problemi di matto in due mosse, la prima mossa non è uno scacco né una cattura di pezzo. In altre parole, possiamo verificare a mano che se il bianco dà uno scacco o cattura un pezzo il nero ha almeno una replica che impedisce al bianco di dare matto alla mossa successiva.
Questo tipo di problema differisce dai problemi del tipo “il bianco muove e vince”, dato che qui lo scopo non è vincere ma dare matto nel numero di mosse prefissato. Consideriamo per esempio la posizione del diagramma (autore: Yochanan Afek). La consegna è: “il bianco muove e matta in due mosse”. Osserviamo senza troppa fatica che non si può dare matto in una sola mossa. Ed osserviamo anche che, come sempre nei problemi di matto in due mosse, la prima mossa non è uno scacco né una cattura di pezzo. In altre parole, possiamo verificare a mano che se il bianco dà uno scacco o cattura un pezzo il nero ha almeno una replica che impedisce al bianco di dare matto alla mossa successiva.  L’ozio è nemico dell’anima: perciò i fratelli, in tempi stabiliti, devono attendere al lavoro manuale: in altre ore, pure assegnate, alla sacra lettura. E pensino di ripartire bene il tempo tra l’una e l’altra cosa. … E se la necessità del luogo o la povertà li costringe a badare essi stessi ai raccolti, non se ne contristino: perché sono veri monaci appunto quando vivono col lavoro delle loro mani come i nostri padri e gli Apostoli… (Dalla Regola monacorum, San Benedetto, Montecassino circa 535 d.C.)
L’ozio è nemico dell’anima: perciò i fratelli, in tempi stabiliti, devono attendere al lavoro manuale: in altre ore, pure assegnate, alla sacra lettura. E pensino di ripartire bene il tempo tra l’una e l’altra cosa. … E se la necessità del luogo o la povertà li costringe a badare essi stessi ai raccolti, non se ne contristino: perché sono veri monaci appunto quando vivono col lavoro delle loro mani come i nostri padri e gli Apostoli… (Dalla Regola monacorum, San Benedetto, Montecassino circa 535 d.C.)  In questo lavoro propongo ai docenti della scuola secondaria di primo e secondo grado, l’esplorazione e lo studio di due prove rilasciate dall’indagine internazionale OCSE PISA, col software libero di geometria dinamica GeoGebra.
In questo lavoro propongo ai docenti della scuola secondaria di primo e secondo grado, l’esplorazione e lo studio di due prove rilasciate dall’indagine internazionale OCSE PISA, col software libero di geometria dinamica GeoGebra. 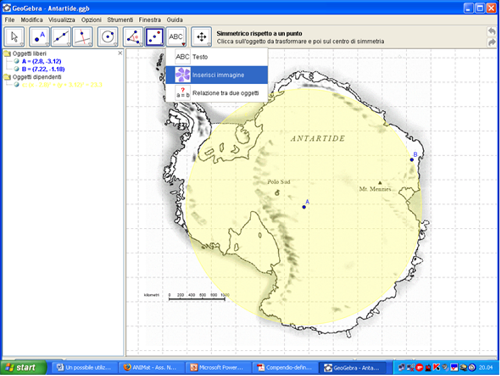
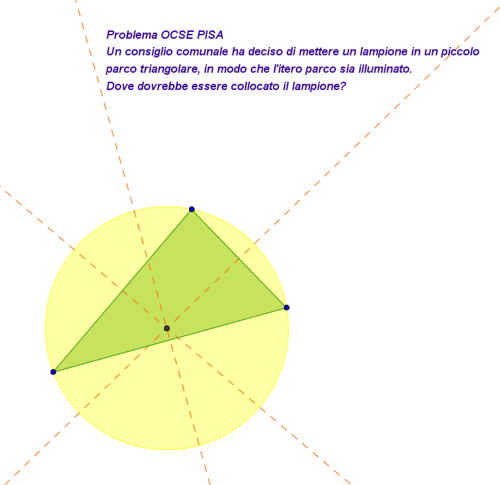
 Il problem solving è tra le attività più importanti che vengono svolte quotidianamente per il semplice fatto che ogni giorno ci si trova ad affrontare situazioni complesse da dover risolvere. Si partirà dal presupposto che il problem solving non è una serie di tecniche da applicare per arrivare ad una soluzione, ma un atteggiamento mentale. Si capisce come, partendo con questa convinzione, nel momento in cui si tratteranno dei problemi in classe l’intenzione dell’insegnante non sarà solo quella di insegnare a risolvere quel problema, o dei problemi, ma di insegnare come ci si approccia ad un problema, come si affronta, come si risolve. Questa tesi partecipa al concorso Condividi la tua tesi e vinci un Aplle iPhone 3G.
Il problem solving è tra le attività più importanti che vengono svolte quotidianamente per il semplice fatto che ogni giorno ci si trova ad affrontare situazioni complesse da dover risolvere. Si partirà dal presupposto che il problem solving non è una serie di tecniche da applicare per arrivare ad una soluzione, ma un atteggiamento mentale. Si capisce come, partendo con questa convinzione, nel momento in cui si tratteranno dei problemi in classe l’intenzione dell’insegnante non sarà solo quella di insegnare a risolvere quel problema, o dei problemi, ma di insegnare come ci si approccia ad un problema, come si affronta, come si risolve. Questa tesi partecipa al concorso Condividi la tua tesi e vinci un Aplle iPhone 3G.  Il seguente lavoro si propone di evidenziare come lo studio della superficie di Marte è un compito che va trattato tramite la combinazione di tecniche di “remote sensing” (telerilevamento), tecniche “in situ” e tecniche di laboratorio quali analisi spettroscopiche di campioni di origine conosciuta; tale integrazione fornisce un’analisi approfondita e univoca del luogo in esame, permettendo di realizzare un metodo complesso di studio che consenta di eliminare a priori le ambiguità derivanti dalla sola analisi spettroscopica dall’orbita. Questa tesi partecipa al concorso Condividi la tua tesi e vinci un Aplle iPhone 3G.
Il seguente lavoro si propone di evidenziare come lo studio della superficie di Marte è un compito che va trattato tramite la combinazione di tecniche di “remote sensing” (telerilevamento), tecniche “in situ” e tecniche di laboratorio quali analisi spettroscopiche di campioni di origine conosciuta; tale integrazione fornisce un’analisi approfondita e univoca del luogo in esame, permettendo di realizzare un metodo complesso di studio che consenta di eliminare a priori le ambiguità derivanti dalla sola analisi spettroscopica dall’orbita. Questa tesi partecipa al concorso Condividi la tua tesi e vinci un Aplle iPhone 3G.  Per il quinto anno consecutivo Caterpillar, il noto programma di Radio2 in onda tutti i giorni dalle 18 alle 19.30 lancia per il 13 febbraio 2009 "M’illumino di meno", una giornata di mobilitazione internazionale in nome del risparmio energetico.
Per il quinto anno consecutivo Caterpillar, il noto programma di Radio2 in onda tutti i giorni dalle 18 alle 19.30 lancia per il 13 febbraio 2009 "M’illumino di meno", una giornata di mobilitazione internazionale in nome del risparmio energetico.  Scopo di questa tesi è quello di presentare alcuni problemi di ottimizzazione in ambito didattico. Si definisce il classico problema isoperimetrico in uno spazio euclideo e si danno alcuni argomenti elementari per la sua risoluzione in un piano euclideo. Infine, si riportano i dati raccolti in alcune scuole di istruzione secondaria superiore presso le quali è stato proposto un questionario riportante alcuni problemi di ottimizzazione. Questa tesi partecipa al concorso "Condividi la tua tesi e vinci un Apple IPhone 3G"
Scopo di questa tesi è quello di presentare alcuni problemi di ottimizzazione in ambito didattico. Si definisce il classico problema isoperimetrico in uno spazio euclideo e si danno alcuni argomenti elementari per la sua risoluzione in un piano euclideo. Infine, si riportano i dati raccolti in alcune scuole di istruzione secondaria superiore presso le quali è stato proposto un questionario riportante alcuni problemi di ottimizzazione. Questa tesi partecipa al concorso "Condividi la tua tesi e vinci un Apple IPhone 3G"  Il biano muove e vince. Questo studio ha origine da una partita giocata tra Fenton e Potter nel 1875. Quando Potter morì nel 1895, G.E. Barbier pubblicò una posizione che derivava dalla Fenton-Potter salvo per la posizione del re (Barbier non ricordava bene la posizione) dichiarando che si trattava di un “il bianco muove e patta”. Ma poi Saavedra rimarcò che in realtà esisteva una variante vincente.
Il biano muove e vince. Questo studio ha origine da una partita giocata tra Fenton e Potter nel 1875. Quando Potter morì nel 1895, G.E. Barbier pubblicò una posizione che derivava dalla Fenton-Potter salvo per la posizione del re (Barbier non ricordava bene la posizione) dichiarando che si trattava di un “il bianco muove e patta”. Ma poi Saavedra rimarcò che in realtà esisteva una variante vincente.  Il sudoku è un gioco logico-matematico che ha ormai tanti appassionati nel mondo. Matematicamente.it propone periodicamente sudoku di diversa difficoltà. Per questo mese:
Il sudoku è un gioco logico-matematico che ha ormai tanti appassionati nel mondo. Matematicamente.it propone periodicamente sudoku di diversa difficoltà. Per questo mese: Scrive lo storico inglese Peter Brown: "Se nella fase di passaggio dal paganesimo al cristianesimo i compiti del filosofo e del vescovo vengono a sovrapporsi, che cosa fa il vescovo, se non eliminare il filosofo?"
Scrive lo storico inglese Peter Brown: "Se nella fase di passaggio dal paganesimo al cristianesimo i compiti del filosofo e del vescovo vengono a sovrapporsi, che cosa fa il vescovo, se non eliminare il filosofo?"  M. è un alunno affetto da dislessia inserito in una classe quarta. Dopo aver conseguito, con un anno di ritardo per aver ripetuto la classe terza, il diploma di qualifica in operatore servizi di cucina, frequenta il biennio per conseguire la qualifica di secondo livello in tecnico servizi ristorativi. La dislessia gli è stata diagnosticata in 3-4 elementare e quindi gli è stato assegnato da subito un docente di sostegno. Questa tesi partecipa al concorso Condividi la tua tesi e vinci un Apple I-Phone 3G.
M. è un alunno affetto da dislessia inserito in una classe quarta. Dopo aver conseguito, con un anno di ritardo per aver ripetuto la classe terza, il diploma di qualifica in operatore servizi di cucina, frequenta il biennio per conseguire la qualifica di secondo livello in tecnico servizi ristorativi. La dislessia gli è stata diagnosticata in 3-4 elementare e quindi gli è stato assegnato da subito un docente di sostegno. Questa tesi partecipa al concorso Condividi la tua tesi e vinci un Apple I-Phone 3G.  Alessandria d’Egitto era diventata fin dalla sua fondazione, un florido centro di valentissimi tecnici, ivi affluiti per dirigere la costruzione della città. In breve tempo essi realizzarono una vera e propria scuola superiore d’ingegneria, ben organizzata e altamente specializzata.
Alessandria d’Egitto era diventata fin dalla sua fondazione, un florido centro di valentissimi tecnici, ivi affluiti per dirigere la costruzione della città. In breve tempo essi realizzarono una vera e propria scuola superiore d’ingegneria, ben organizzata e altamente specializzata.  L’intento è mostrare quali siano i risultati conseguibili in una classe dove l’insegnante decide di adottare un approccio socio-costruttivista, ovvero propone attività che consentano la costruzione degli apprendimenti da parte dei bambini, riconosciuti come individui attivi e competenti e inseriti in un contesto sociale e culturale interattivo. Più in particolare l’interesse si focalizza sui vantaggi che si possono riscontrare conducendo un percorso geometrico imperniato sulla didattica per problemi, che fa quindi del problema il suo elemento cardine. Questa tesi partecipa al concorso "Condividi la tua tesi e vinci un Apple Iphone 3G"
L’intento è mostrare quali siano i risultati conseguibili in una classe dove l’insegnante decide di adottare un approccio socio-costruttivista, ovvero propone attività che consentano la costruzione degli apprendimenti da parte dei bambini, riconosciuti come individui attivi e competenti e inseriti in un contesto sociale e culturale interattivo. Più in particolare l’interesse si focalizza sui vantaggi che si possono riscontrare conducendo un percorso geometrico imperniato sulla didattica per problemi, che fa quindi del problema il suo elemento cardine. Questa tesi partecipa al concorso "Condividi la tua tesi e vinci un Apple Iphone 3G"  Questo studio dimostra che nei finali di pedoni l’aspetto che ha la strategia vincente è per lo più matematico: non ci sono mosse intuitive e si è permeati da una sana inevitabilità. Per giocare a
Questo studio dimostra che nei finali di pedoni l’aspetto che ha la strategia vincente è per lo più matematico: non ci sono mosse intuitive e si è permeati da una sana inevitabilità. Per giocare a 


 Ci preparammo con impegno… Ma sembrava che ogni volta che cominciavamo a formare una squadra saremmo stati riorganizzati. La vita poi mi insegnò che tendiamo ad affrontare qualsiasi situazione riorganizzandoci: che modo meraviglioso per dare l’illusione di progresso, mentre si crea soltanto confusione, inefficienza e demoralizzazione. (Petronio Arbitro)
Ci preparammo con impegno… Ma sembrava che ogni volta che cominciavamo a formare una squadra saremmo stati riorganizzati. La vita poi mi insegnò che tendiamo ad affrontare qualsiasi situazione riorganizzandoci: che modo meraviglioso per dare l’illusione di progresso, mentre si crea soltanto confusione, inefficienza e demoralizzazione. (Petronio Arbitro)  Il 5° gioco di società che prende spunto dalla Teoria dei Giochi. L’idea è molto semplice. Si tratta di distribuire caramelle a un gruppo di bambini. Solo che il modo di distribuirle crea un bel conflitto fra un vantaggio immediato ed uno, possibile, futuro ma mediato dalla fiducia reciproca. Fiducia che è messa a forte rischio!
Il 5° gioco di società che prende spunto dalla Teoria dei Giochi. L’idea è molto semplice. Si tratta di distribuire caramelle a un gruppo di bambini. Solo che il modo di distribuirle crea un bel conflitto fra un vantaggio immediato ed uno, possibile, futuro ma mediato dalla fiducia reciproca. Fiducia che è messa a forte rischio!  Come spesso accade per molte importanti scoperte, un team di ricercatori della NASA, mentre era intento nello studio del comportamento di alcune nebulose, si è invece accidentalmente imbattuto nella scoperta di un gruppo di stelle che sembrano schizzare via a velocità impressionante nello spazio.
Come spesso accade per molte importanti scoperte, un team di ricercatori della NASA, mentre era intento nello studio del comportamento di alcune nebulose, si è invece accidentalmente imbattuto nella scoperta di un gruppo di stelle che sembrano schizzare via a velocità impressionante nello spazio. 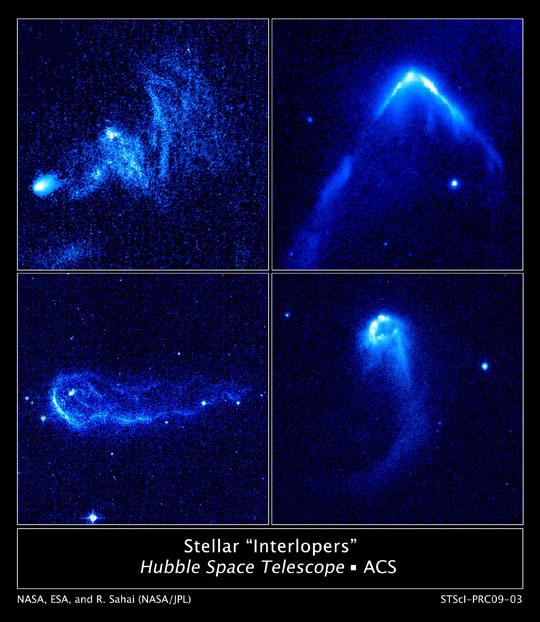
 In arrivo la pagella del primo quadrimestre con un significativo cambiamento del voto in condotta: il voto in condotta contribuisce alla valutazione complessiva dello studente, chi a fine anno non ha 6 in condotta non è ammesso alla classe successiva.
In arrivo la pagella del primo quadrimestre con un significativo cambiamento del voto in condotta: il voto in condotta contribuisce alla valutazione complessiva dello studente, chi a fine anno non ha 6 in condotta non è ammesso alla classe successiva.  All’inizio dei corsi che compongono il biennio di specializzazione SIS avevo venticinque anni e provenivo da quella scuola che “forma” le menti scientifiche dei suoi allievi utilizzando il dogma empirico. Io stesso ho provato sulla mia pelle l’ebbrezza della tipica consegna “e ora ditemi cosa osservate”. In questo la SIS mi ha piacevolmente stupito. Perché sono rimasto gradevolmente sorpreso da quanto ho appreso durante la SIS? Perché l’ho trovato utile per il mio futuro! Voglio provare ad argomentare questa mia asserzione. [Questa tesi partecipa al concorso "Condividi la tua tesi e vinci un iPhone 3G"]
All’inizio dei corsi che compongono il biennio di specializzazione SIS avevo venticinque anni e provenivo da quella scuola che “forma” le menti scientifiche dei suoi allievi utilizzando il dogma empirico. Io stesso ho provato sulla mia pelle l’ebbrezza della tipica consegna “e ora ditemi cosa osservate”. In questo la SIS mi ha piacevolmente stupito. Perché sono rimasto gradevolmente sorpreso da quanto ho appreso durante la SIS? Perché l’ho trovato utile per il mio futuro! Voglio provare ad argomentare questa mia asserzione. [Questa tesi partecipa al concorso "Condividi la tua tesi e vinci un iPhone 3G"]  I punti notevoli del triangolo sono stati i protagonisti di una notevole quantità di articoli e libri , la cui produzione toccò il suo massimo a fine ’800. Recentemente alcuni matematici come, per esempio, R.Kimberling, hanno ritrovato interesse per i punti notevoli del triangolo. Sorprendentemente, invece, non sono stati portati avanti analoghi studi sui punti notevoli del quadrangolo e del quadrilatero. Per il quadrilatero completo (quattro lati e sei vertici) si può fare riferimento ai contributi di G. Steiner; mentre per quanto riguarda il quadrangolo completo (quattro vertici e sei lati) la bibliografia si riduce a qualche decina di articoli, tra loro disconnessi. Uno studio sistematico di questo argomento è stato fatto da B. Scimemi, che si è avvalso anche della collaborazione di alcuni suoi studenti. Qui si trova la descrizione e lo studio delle proprietà di alcuni punti notevoli del quadrangolo completo.
I punti notevoli del triangolo sono stati i protagonisti di una notevole quantità di articoli e libri , la cui produzione toccò il suo massimo a fine ’800. Recentemente alcuni matematici come, per esempio, R.Kimberling, hanno ritrovato interesse per i punti notevoli del triangolo. Sorprendentemente, invece, non sono stati portati avanti analoghi studi sui punti notevoli del quadrangolo e del quadrilatero. Per il quadrilatero completo (quattro lati e sei vertici) si può fare riferimento ai contributi di G. Steiner; mentre per quanto riguarda il quadrangolo completo (quattro vertici e sei lati) la bibliografia si riduce a qualche decina di articoli, tra loro disconnessi. Uno studio sistematico di questo argomento è stato fatto da B. Scimemi, che si è avvalso anche della collaborazione di alcuni suoi studenti. Qui si trova la descrizione e lo studio delle proprietà di alcuni punti notevoli del quadrangolo completo.  Il prossimo 30 gennaio 2009, si verificherà una congiunzione tra la Luna e Venere. I due astri saranno visibili, poco dopo il tramonto, in direzione Ovest. La Luna sarà una sottile falce ulluminata per il 18%, Venere invece, brillantissima come sempre, sarà appena 4 gradi sotto il nostro satellite. Si prennuncia come uno spettacolo carino da osservare e da fotografare. Potete farlo con una qualsiasi fotocamera, anche compatta, ed un treppiede.
Il prossimo 30 gennaio 2009, si verificherà una congiunzione tra la Luna e Venere. I due astri saranno visibili, poco dopo il tramonto, in direzione Ovest. La Luna sarà una sottile falce ulluminata per il 18%, Venere invece, brillantissima come sempre, sarà appena 4 gradi sotto il nostro satellite. Si prennuncia come uno spettacolo carino da osservare e da fotografare. Potete farlo con una qualsiasi fotocamera, anche compatta, ed un treppiede. 

 Perché il Signore agirà come un uomo che partendo per un viaggio chiamò i suoi servi e consegnò loro i suoi beni. Ad uno diede cinque talenti, ad un altro due, ad un terzo uno: a ciascuno secondo la capacità sua; e subito partì. Quegli che aveva ricevuto cinque talenti li negoziò e ne guadagnò altri cinque. Così pure quello che ne aveva avuti due, ne guadagnò altri due; ma quello che ne aveva ricevuto solo uno, andò fece una buca in terra e vi nascose il denaro del suo padrone.
Perché il Signore agirà come un uomo che partendo per un viaggio chiamò i suoi servi e consegnò loro i suoi beni. Ad uno diede cinque talenti, ad un altro due, ad un terzo uno: a ciascuno secondo la capacità sua; e subito partì. Quegli che aveva ricevuto cinque talenti li negoziò e ne guadagnò altri cinque. Così pure quello che ne aveva avuti due, ne guadagnò altri due; ma quello che ne aveva ricevuto solo uno, andò fece una buca in terra e vi nascose il denaro del suo padrone.  Scopo del gioco è trovare una strada tra i numeri seguendo la regola aritmetica indicata in alto a sinistra sullo schermo. Partendo dal numero in basso a sinistra cerca di raggiungere il numero in alto a destra: puoi andare su, giù, in diagonale, non puoi saltare.
Scopo del gioco è trovare una strada tra i numeri seguendo la regola aritmetica indicata in alto a sinistra sullo schermo. Partendo dal numero in basso a sinistra cerca di raggiungere il numero in alto a destra: puoi andare su, giù, in diagonale, non puoi saltare.

 Anna Cerasoli è nota al grande pubblico per i suoi libri divulgativi di matematica I magnifici 10, La sorpresa dei numeri, Mr Quadrato, pubblicati anche all’estero. Le abbiamo fatto alcune domande sul suo nuovo libro.
Anna Cerasoli è nota al grande pubblico per i suoi libri divulgativi di matematica I magnifici 10, La sorpresa dei numeri, Mr Quadrato, pubblicati anche all’estero. Le abbiamo fatto alcune domande sul suo nuovo libro. 
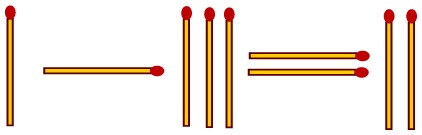
 Poteva mancare il dilemma del prigioniero? Certo che no! La proposta è di giocarlo “al plurale”. Ovvero, si gioca a squadre: qui parleremo di squadra I contro la squadra II, ma nulla vieta di scegliere nomi più “immaginifici” o più appropriati a secondo del contesto, incluso il fantozziano “scapoli-ammogliati”. Alla fine del gioco, c’è spazio per litigate, come a tressette o a scopa. Oltre che giocarlo a gruppi, si suggerisce anche di giocare una sorta di dilemma del prigioniero ripetuto, cioè di giocare più di un turno. Tutti i dettagli necessari sono forniti sotto.
Poteva mancare il dilemma del prigioniero? Certo che no! La proposta è di giocarlo “al plurale”. Ovvero, si gioca a squadre: qui parleremo di squadra I contro la squadra II, ma nulla vieta di scegliere nomi più “immaginifici” o più appropriati a secondo del contesto, incluso il fantozziano “scapoli-ammogliati”. Alla fine del gioco, c’è spazio per litigate, come a tressette o a scopa. Oltre che giocarlo a gruppi, si suggerisce anche di giocare una sorta di dilemma del prigioniero ripetuto, cioè di giocare più di un turno. Tutti i dettagli necessari sono forniti sotto. 





 L’ONU ha proclamato l’anno 2009 “Anno Internazionale dell’Astronomia”, accogliendo così la mozione che l’UNESCO aveva già avanzato nel dicembre 2005. Questa proclamazione è anche un successo italiano, poiché è stato proprio il nostro Paese il primo a farsene promotore fin dal 2003. Un risultato raggiunto anche grazie al fatto che nel 2009 ricorre il IV centenario dalla prima osservazione del cielo con un cannocchiale, da parte di Galileo Galilei.
L’ONU ha proclamato l’anno 2009 “Anno Internazionale dell’Astronomia”, accogliendo così la mozione che l’UNESCO aveva già avanzato nel dicembre 2005. Questa proclamazione è anche un successo italiano, poiché è stato proprio il nostro Paese il primo a farsene promotore fin dal 2003. Un risultato raggiunto anche grazie al fatto che nel 2009 ricorre il IV centenario dalla prima osservazione del cielo con un cannocchiale, da parte di Galileo Galilei. 

 In questo lavoro propongo un’attività didattica per studenti della scuola media o del primo biennio superiore. L’obiettivo è quello d’introdurre lo studio delle proprietà dei quadrilateri attraverso la lettura di un racconto di fantasia che incuriosisca i ragazzi. In una fase successiva essi dovranno individuare delle figure, disegnarle (con riga e compasso o con software di geometria dinamica) ed esplorarne le proprietà. In tutte le fasi il docente guiderà la discussione con la classe fino a pervenire alla sistemazione teorica dei contenuti.
In questo lavoro propongo un’attività didattica per studenti della scuola media o del primo biennio superiore. L’obiettivo è quello d’introdurre lo studio delle proprietà dei quadrilateri attraverso la lettura di un racconto di fantasia che incuriosisca i ragazzi. In una fase successiva essi dovranno individuare delle figure, disegnarle (con riga e compasso o con software di geometria dinamica) ed esplorarne le proprietà. In tutte le fasi il docente guiderà la discussione con la classe fino a pervenire alla sistemazione teorica dei contenuti. 

