ESERCIZIO 3: Semplificare la frazione
![]()
la scrivo in questo modo![]()
la risolvo in questo modo

FINE.
ESERCIZIO 3: Semplificare la frazione
![]()
la scrivo in questo modo![]()
la risolvo in questo modo

FINE.
ESERCIZIO 2: Semplificare la frazione
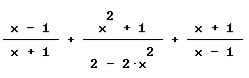
la scrivo in questo modo
![]()
la risolvo in questo modo
FINE.
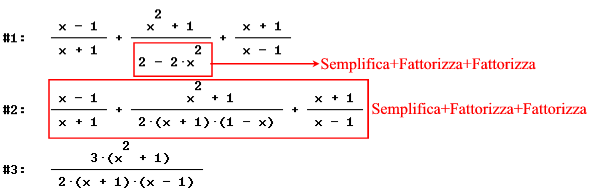
ESERCIZIO 1: Semplificare la frazione
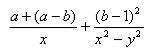
Avvia Derive. Per scrivere l’espressione, presta molta attenzione all’uso delle parentesi. La scrittura corretta è
![]()
Derive visualizza
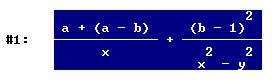
Clicca più volte sul segno "+" del numeratore della prima frazione fino a ottenere la selezione
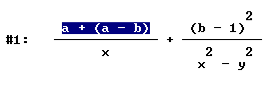
Clicca sul segno uguale posto nella barra dei comandi
Ottieni
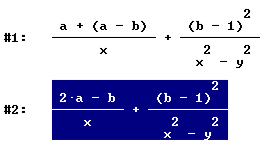
Seleziona il numeratore della seconda frazione puntando con il mouse il segno "-". Ottieni
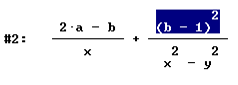
Quindi "Semplifica" "Sviluppa"
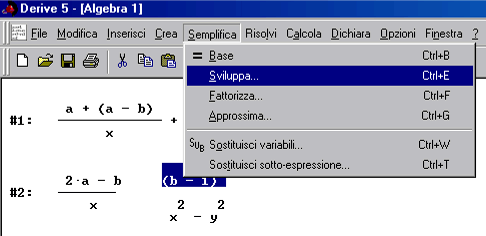
Ancora il bottone "Sviluppa)
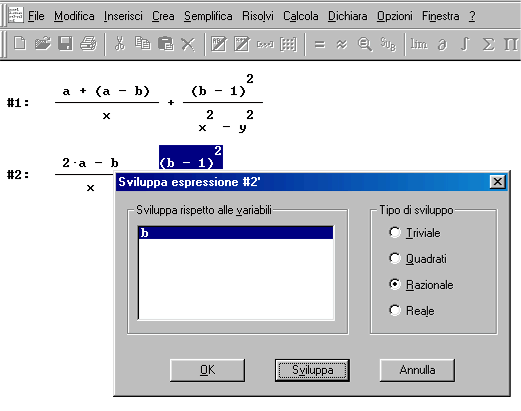
ottieni lo sviluppo del quadrato del binomio
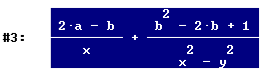
Per scomporre in fattori il denominatore della seconda frazione, selezionalo e poi premi i bottoni "Semplifica" "Fattorizza"
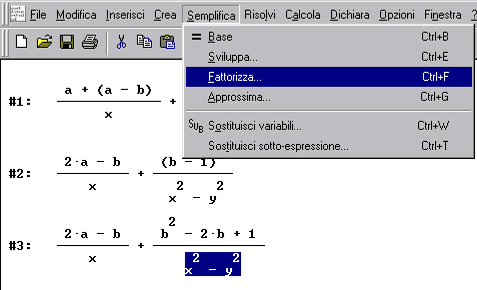
ancora sul pulsante "Fattorizza"
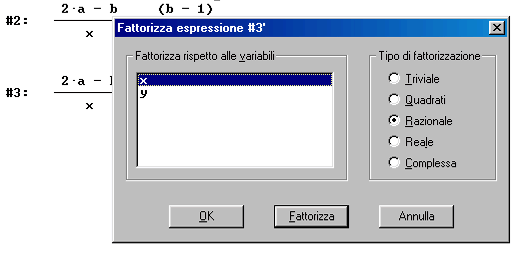
Ottieni la scomposizione in fattori della differenza di quadrati
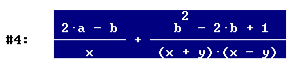
"Semplifica", "Fattorizza", "Fattorizza" ottieni
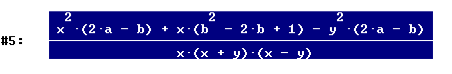
osserva che il prodotto (x+y)(x-y)(2a-b) è stato eseguito come (x2 -y2 )(2a-b) e sviluppato in due parti, una all’inizio e l’altra alla fine dell’espressione
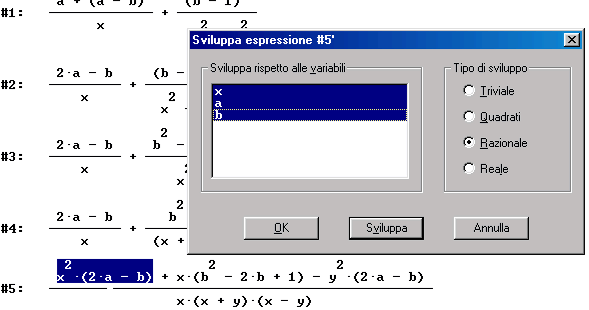
Seleziona il primo prodotto da sviluppare ed esegui i comandi "Semplifica", "Sviluppa" con il mouse seleziona tutte le variabili e premi il pulsante "Sviluppa". Ottieni

Sviluppa gli altri due prodotti del numeratore, ottieni
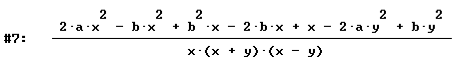
FINE
ESERCIZIO 3: Calcola il valore della seguente espressione
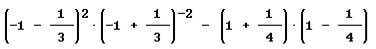
la scrivo in questo modo

la risolvo in questo modo, in blu sono indicate le operazioni da selezionare, quindi, dalla barra dei comandi "Semplifica" "Base"
FINE.
ESERCIZIO 2: Calcola il valore della seguente espressione
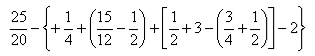
la scrivo in questo modo
![]()
la risolvo in questo modo
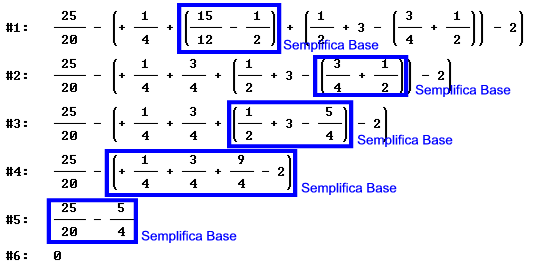
FINE.
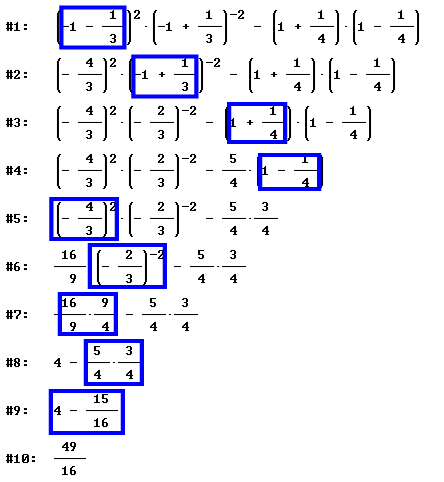
ESERCIZIO 1: Calcola il valore della seguente espressione
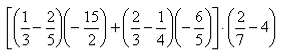
Avvia Derive. Per scrivere l’espressione, presta molta attenzione all’uso delle parentesi. La scrittura corretta è
![]()
Comincia dalla prima parentesi tonda puntando con il mouse il segno meno e cliccando più volte fino a ottenere
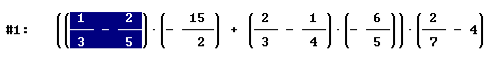
Quindi, clicca su "Semplifica" e poi su "Base"
Ottieni
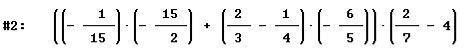
Seleziona il segno "-" dell’operazione da eseguire. Ottieni
![]()
Quindi "Semplifica" "Base"
ottieni
![]()
Seleziona l’operazione di sottrazione dell’ultima parentesi. Quindi ripeti la procedura "Semplifica" "Base". Ottieni
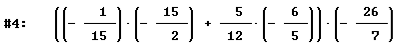
Seleziona la prima operazione di moltiplicazione puntandola con il mouse e cliccando più volte

Ripeti i comandi "Semplifica" "Base". Ottieni
![]()
Punta ancora la prima operazione di moltiplicazione, cliccando ottieni
![]()
"Semplifica" "Base"
![]()
La scrittura non è formalmente corretta, il primo segno "+" è superfluo. Seleziona la prima parentesi
![]()
"Semplifica" "Base", ottieni
![]()
Dovresti già sapere che il risultato del prodotto è 0. Comunque, seleziona l’operazione, quindi "Semplifica" "Base"
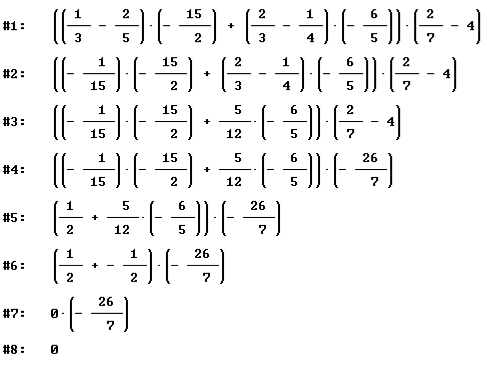
Non ti resta che stamparla e ricopiarla sul quaderno.
FINE
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
Scarica il file in formato XLS
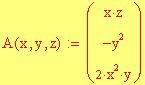
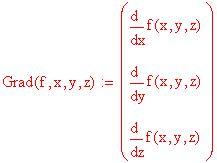
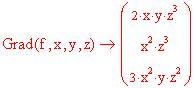
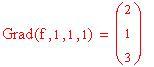
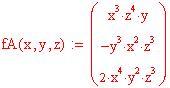
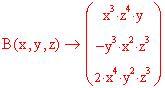
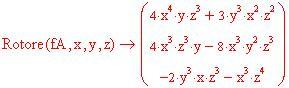
x0 ,y0 coordinate del punto proiezione sul piano xy del punto di tangenza
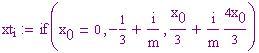
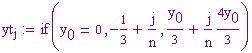
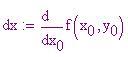
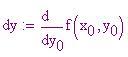
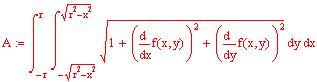
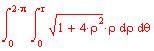
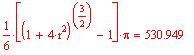
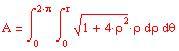
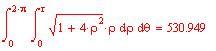
Metodo di Monte Carlo per l'Integrazione Numerica con Mathcad
(Carlo Elce)
In questa sezione illustreremo un metodo per l'integrazione numerica mediante la simulazione (generazione di numeri casuali).
Immettiamo le funzioni che rappresentano la frontiera della regione dove vogliamo definire la funzione di due variabili reali da integrare
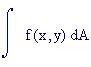
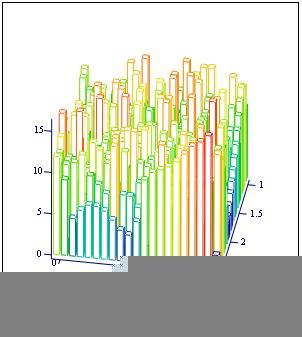
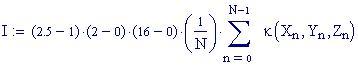
Per vedere come varia il calcolo numerico dell’integrale al variare di N cliccate qui
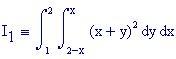
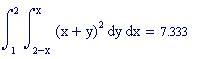
Definiamo la frontiera della regione del piano x-y :
A ssumiamo e
per ogni x .
Integrali Doppi variabili calcolati numericamente ( Carlo Elce )
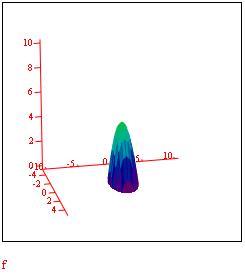
Partendo da una funzione, che rappresenta un piano variabile parallelo al piano x-y su cui è definito un dominio quadrato, viene evidenziato come un integrale doppio calcoli il volume di un parallelepipedo. Facendo poi variare la funzione e il dominio piano viene mostrato come l’integrale doppio calcoli il volume di un solido delimitato da una superficie più generale .
.
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
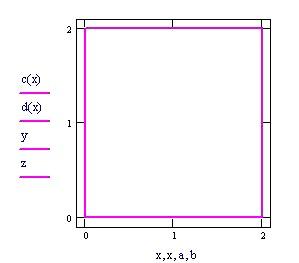
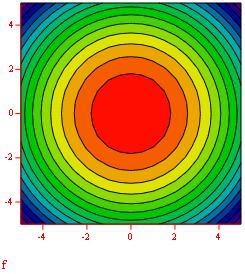
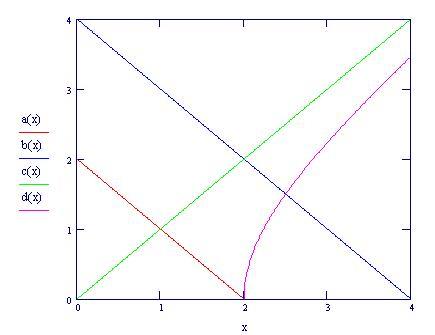
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L’ integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l’animazione clicca sul grafico seguente

Definiamo una nuova funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
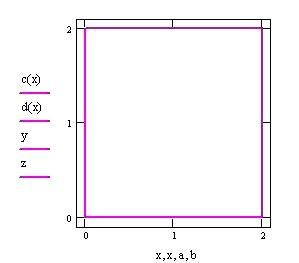
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L’ integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l’animazione clicca sul grafico seguente
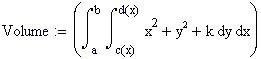
Definiamo una terza funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
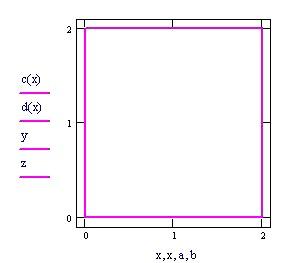
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L’ integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l’animazione clicca sul grafico seguente
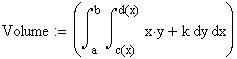
Definiamo una nuova frontiera della regione del piano x-y :
assumiamo e
per ogni x .
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
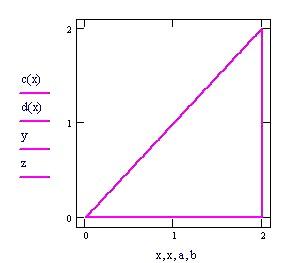
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L’ integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l’animazione clicca sul grafico seguente
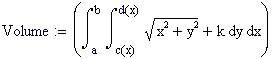
Definiamo una nuova frontiera della regione del piano x-y :
assumiamo e
per ogni x .
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
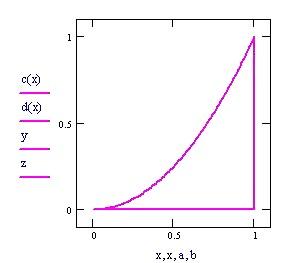
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L’ integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l’animazione clicca sul grafico seguente
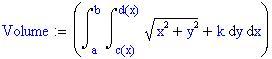
Definiamo una nuova frontiera della regione del piano n x-y :
assumiamo e
per ogni x.
Definiamo la funzione di due variabili reali da integrare e una variabile temporale FRAME per parametrizzare la funzione:
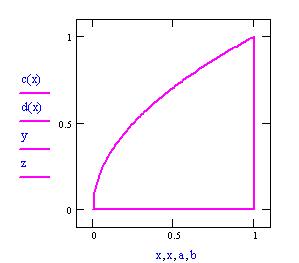
Grafico della frontiera del dominio piano in cui definiamo la funzione f(x,y).
L’ integrale doppio calcola il volume delimitato dal dominio piano e dalla superficie rappresentata dalla funzione f(x,y).
Per vedere l’animazione clicca sul grafico seguente
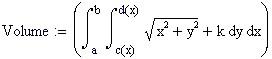
Visita anche la sezione di Analisi matematica, appunti sugli integrali, esercizi sugli integrali, esercizio di integrale doppio, integrale triplo, integrale improprio
In questa sezione illustreremo come la decomposizione di una funzione razionale fratta in fratti semplici consente di calcolare facilmente l'integrale della funzione data.
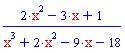
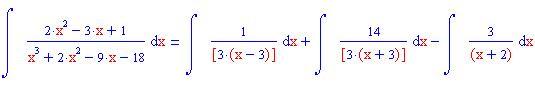
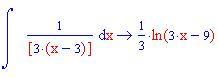
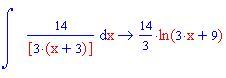
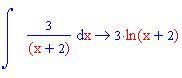
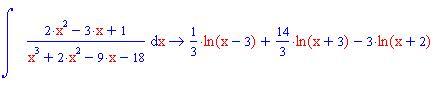
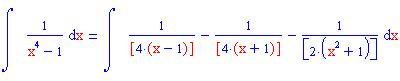
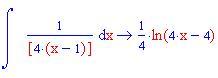
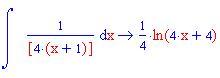
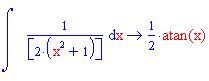
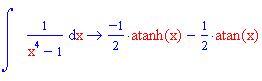
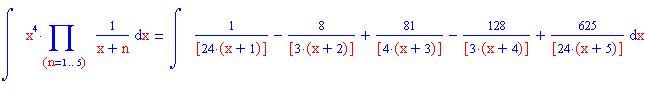
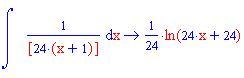
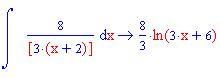
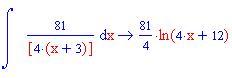
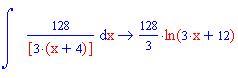

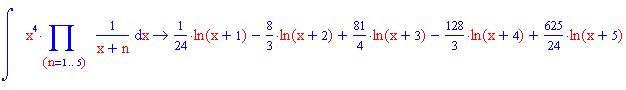
Calcolo della lunghezza di un arco di curva di una funzione continua insieme alle sue derivate
In questa sezione calcoleremo la lunghezza di un arco di curva di una funzione definita in un intervallo continua insieme alle sue derivate.
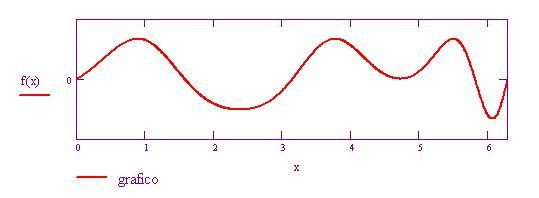
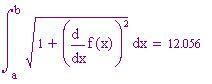
Cosa succederebbe all'arco di curva se pensassimo di far variare l'estremo superiore b dell'intervallo considerato?
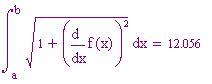 __________________________________________________________________________
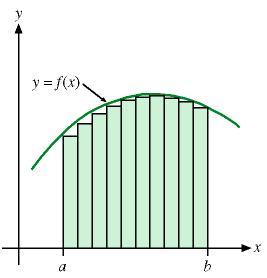
__________________________________________________________________________Per stimare l'area tra l'asse x e il grafico di una funzione non negativa f(x) in un intervallo [a, b], definiamo una partizione di [a, b] scegliendo n–1 punti x 1 , x 2 , . . ., x n –1 in [a, b], a = x 0 x 1 . . . x n –1 b = x n . Su ciascun subintervallo [x k –1 , x k ] costruiamo un rettangolo di larghezza Dx k = x k – x k –1 di altezza rispetto all'asse x uguale a f(c k ) . Il lato superiore di ciascun rettangolo deve toccare la curva in un punto (c k , f(c k )).
Sommando le aree di tutti i rettangoli, otteniamo un valore approssimato dell'area compresa tra l'asse x e f(x).
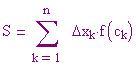
è chiamata somma di Riemann per f nell'intervallo [a, b].
Trova una somma di Riemann per D(r) = 1/r nell'intervallo [1, 10].
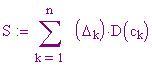
Rappresentazione grafica:
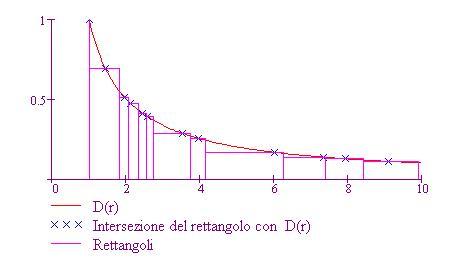
Nota che diciamo di aver calcolato una somma di Riemann, piuttosto che la somma di Riemann. La somma dipende dalla partizione e dalla scelta dei punti c k in cui si valuta D(r).
Come ci si può aspettare, aumentando il numero dei rettangoli in una somma di Riemann si ottiene un valore approssimato con maggior precisione dell'area. Comunque, questo è vero solo se l'ampiezza del rettangolo più largo della partizione, chiamata norma della partizione, diventa sempre più piccola ossia tende a zero.
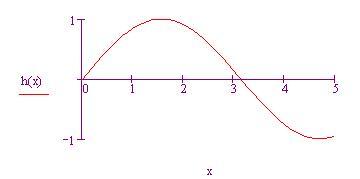
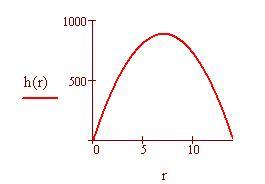
h(x) è non negativa in [0, p ] e negativa in ( p , 5]. Costruiamo due somme di Riemann, la prima sommando le aree dei rettangoli nella partizione di [0, p ] e la seconda sommando le opposte delle aree dei rettangoli nella partizione di [ p , 5].
Usiamo l'estremo sinistro di ciascun subintervallo per definire i vari rettangoli.
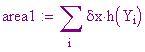
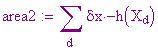
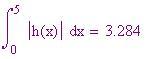
Il problema di trovare area, lunghezze d'arco, centro di massa e lavoro di una forza spesso può essere espresso in termini di integrale di una funzione in un intervallo.
Area della regione tra le curve f 1 (x) e f 2 (x), f 1 (x) f 2 (x) nell'intervallo [a,b]:
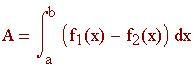
Lunghezza della curva g(x) da a a b :
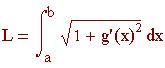
Centro di massa di una barra o una striscia sottile posta lungo l'asse x con funzione densità d(x):
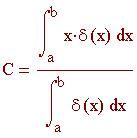
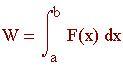
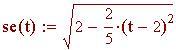 ?
? 
Abbiamo bisogno di conoscere i punti d'intersezione delle curve per determinare gli estremi dell'intervallo d'integrazione. A tale scopo risolviamo l'equazione:
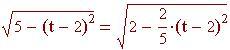
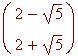
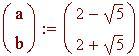
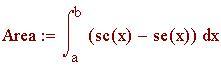
Un razzo è lanciato dal suolo verso l'alto. La sua traiettoria è una parabola. La funzione dà la quota del razzo in metri quando esso ha percorso una distanza orizzontale di x metri. Qual è la misura dell'arco di curva percorso dal raz zo?
Trova dove la quota del razzo è di nuovo 0 per determinare l'estremo superiore dell'integrale.
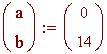
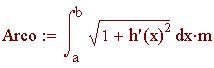
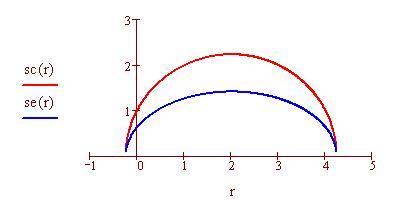
Determina il centro di massa di un'asta di bandiera di 6 metri con una densità che varia linearmente da 3.5 kg/m 3 alla base a 2 kg/m 3 in cima.
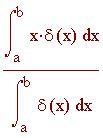
Il denominatore è la massa e il numeratore è il momento rispetto all'origine.

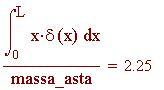
Uno spargitore di 7 chilogrammi riempito con 4.5 chilogrammi di sale e sabbia è spinto lungo un marciapiede ghiacciato. Se assumiamo che lo spargitore si svuota su una distanza di 70 metri con un tasso costante, quanto lavoro viene compiuto per spingere lo spargitore su tale distanza?
Le unità di lavoro sono il prodotto di una unità di forza e una unità di distanza. Joule ed erg sono esempi di unità di lavoro.
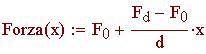
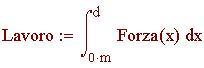
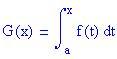 per a x b. Allora G è derivabile in [a, b] e la sua derivata è f; cioè
per a x b. Allora G è derivabile in [a, b] e la sua derivata è f; cioè 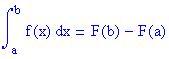
Quello che i Teoremi Fondamentali del Calcolo non garantiscono è che la primitiva di una funzione continua possa essere scritta in termini di funzioni elementari: polinomi, seno, coseno, radici, esponenziali e logaritmi. Essi ci danno, comunque, un semplice metodo per valutare l'integrale permettendoci di scegliere una qualsiasi primitiva della funzione integranda.
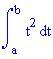
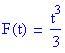 , così che l'integrale è:
, così che l'integrale è: 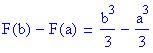
In una sezione precedente, abbiamo valutato questo integrale usando le somme di Riemann e prendendo il limite per la norma della partizione tendente a zero.
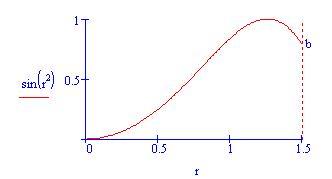
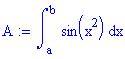
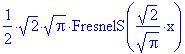
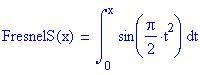
Questo significa che non esiste un'espressione dell'integrale di sin(x 2 ) in termini di funzioni elementari. Il massimo che possiamo fare è calcolare l'integrale numericamente.
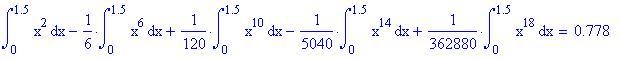
Ovviamente maggiore è l'ordine dello sviluppo in serie della funzione più accurato è il valore dell'area calcolata numericamente!
In questa sezione illustreremo i primi elementi di geometria differenziale relativi alle curve nel piano x-y .
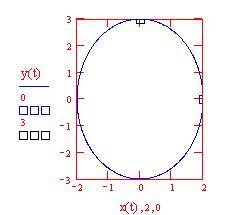
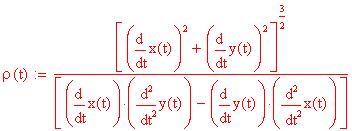
Il raggio del cerchio osculatore (cerchio che meglio approssima la curva) in un punto dell'ellisse è l' inverso della curvatura.
In geometria piana, una retta si dice tangente a una circonferenza se interseca la circonferenza in un solo punto, secante se interseca la circonferenza in due punti, esterna se non ha alcun punto d'intersezione con la circonferenza. Per altri tipi di curve, una retta può intersecarle in un solo punto, ma non essere tangente. Se vogliamo applicare il concetto di tangente ad altre curve diverse dalla circonferenza abbiamo bisogno di una definizione matematica più generale.
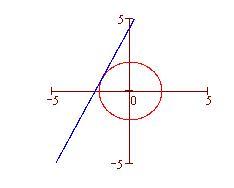
La retta blu è una tangente.
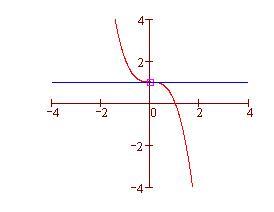
La retta blu è tangente?
Per definire il coefficiente angolare di una tangente usiamo il concetto di limite. Nel file precedente abbiamo definito la retta secante, che passa per due punti della curva. Ora definiamo la retta tangente in un singolo punto (x 0 , f(x 0 )) alla curva f(x) come la retta che passa per P 0 (x 0 , f(x 0 )) il cui coefficiente angolare è il limite, per h tendente a zero, dei coefficienti angolari delle secanti che passano per i punti P 0 (x 0 , f(x 0 )) e P(x 0 +h, f(x 0 +h )).
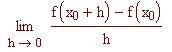
Coefficiente angolare della retta tangente nel punto P 0 (x 0 , f(x 0 )) alla curva f(x):
Troviamo il coefficiente angolare della tangente alla curva nel punto (2, 6).
Valutiamo l'espressione del limite per piccoli valori di h, sia positivi che negativi.
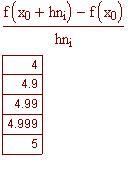

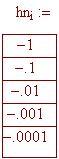
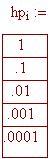
Osservate a quale numero si avvicinano i valori sulle colonne di destra per valori di h tendenti a zero
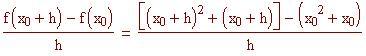
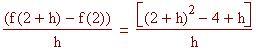
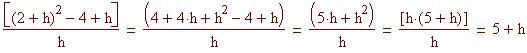
Troviamo il punto sulla curva in cui il coefficiente angolare della tangente è –0.3 . Rappresentiamo graficamente y(t), la retta tangente e la perpendicolare (o normale).
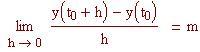
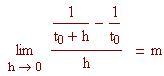
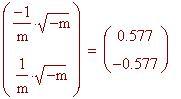
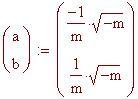
tangenti
e normali
variabili
animazione
a cura di
Carlo Elce
La secante di una curva, che sia il grafico di una funzione, è una retta che passa per due punti distinti della curva. Il coefficiente angolare della secante ci dà la velocità media di variazione della funzione in un intervallo di valori.
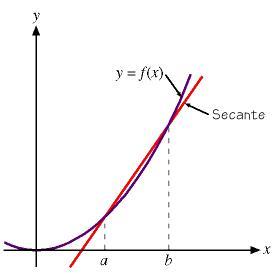
Se f(x) è la funzione a e b sono le ascisse di due punti sulla curva attraverso i quali vogliamo tracciare la secante, allora il coefficiente angolare della secante è:
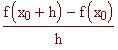 .
. 
Un oggetto lanciato percorre approssimativamente centimetri in t secondi dopo il lancio. Qual è la velocità media dell’oggetto nell’intervallo temporale 1… 4 ? E nell’intervallo 1… 1.5 secondi?
Velocità media tra 1 e 4 secondi:
Il coefficiente angolare della secante è la velocità media dell’oggetto tra i due tempi.
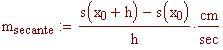
Velocità media tra 1 e 1.5 secondi:
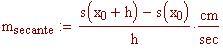
E’ interessante osservare il comportamento della secante quando i due punti si avvicinano.
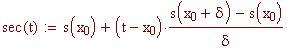
Clicca sul grafico per vedere la variazione del coefficiente angolare della secante
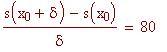
Se il valore di una funzione f(x) si avvicina al valore L quando x si avvicina ad a , diciamo che f(x) ha come limite L per x tendente ad a.
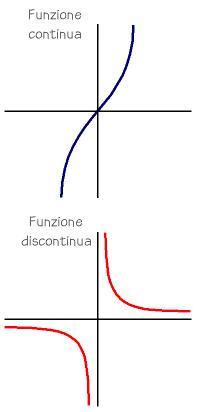
Affinchè f(x) abbia limite L quando x si avvicina ad a, devono esistere il limite destro e il limite sinistro per x tendente ad a e devono essere uguali. Con notazione matematica
C'è differenza tra un limite che esiste in un punto del dominio di una funzione e la continuità della funzione nel punto? Sì. La continuità impone una condizione più forte. Infatti, perché un limite esista è irrilevante che il valore della funzione esista in x = a, o anche che appartenga al dominio della funzione. Per la continuità, noi dobbiamo poter valutare la funzione in a, e il valore f(a) deve coincidere con il limite di f(x) in a.
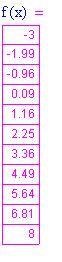
1. Definiamo una lista di valori che si avvicini ad a e calcoli il valore della funzione in ciascuno di questi punti.
Se i valori della funzione si avvicinano quanto si vuole ad un unico numero, quel numero è il limite.
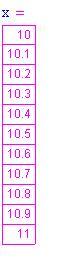
2. Se le funzioni sono polinomi, radici, seni, coseni, esponenziali, o una combinazione algebrica di queste funzione (somma, differenza, prodotto, o quoziente), proviamo a sostituire il numero a cui tende la variabile indipendente per ottenere il limite.
Se quel valore non è ¥ o – ¥ , e l'espressione del limite non si pone nella forma 0/0 o ¥ / ¥ , allora abbiamo raggiunto il risultato.
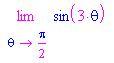
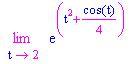
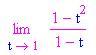
Che succede se la variabile tende a ¥ o – ¥ ? Nessun problema se non troviamo forme indeterminate 0/0 o ¥ / ¥ .
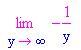
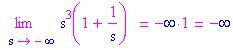
Se quando sostituiamo otteniamo 0/0 o ¥ / ¥ proviamo a scomporre in fattori per tentare di eliminare l'indeterminazione.
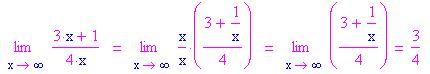
Questo è un caso in cui ottieni una risposta equivoca. Questo limite non esiste! Ciò succede perché la funzione coseno è periodica e così assume tutti i valori compresi tra –1 e 1 .
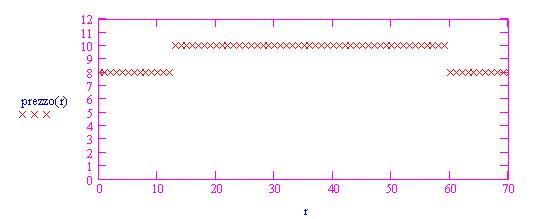
Poiché questi limiti sono diversi, prezzo(w) non ha il limite per w tendente a 12. Ciò risponde esaurientemente alla domanda sulla continuità: prezzo(w) non è continua per w = 12; sebbene prezzo(12) sia definita, il limite per w tendente a 12 non esiste.