I satelliti che orbitano attorno alla Terra restano in movimento grazie alle stesse leggi che governano il moto dei pianeti attorno al sole, cioè le leggi di Keplero. Le orbite dei satelliti sono orbite ellittiche, di cui la Terra occupa uno dei due fuochi.
Per semplicità, si considerano le orbite dei satelliti circolari, la Terra di forma sferica e massa uniforme, e il satellite come corpo puntiforme.
Il meccanismo con cui una satellite viene messo in orbita può essere spiegato considerando un razzo che viene sparato verso l’alto da un determinato punto della superficie terrestre.
Quando il razzo si trova ad una determinata distanza dalla superficie, esso spara orizzontalmente un proiettile, imprimendogli quindi una velocità che ha direzione perpendicolare a quella della superficie terrestre.
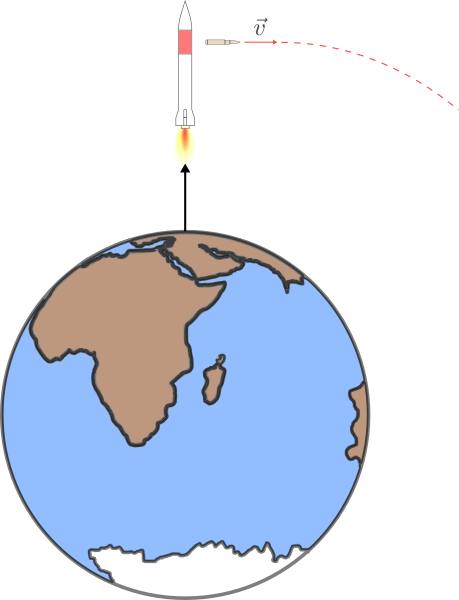
La velocità che viene impresa al proiettile è tale da permettere al proiettile di continuare ad orbitare attorno alla Terra senza cadere giù. Infatti, sebbene il proiettile è costantemente attratto dalla forza gravitazionale, la superficie sferica della Terra fa si che il proiettile riesca sempre a sfuggirli sotto, senza cadere su di essa.
Notiamo che la velocità che viene impressa inizialmente al proiettile deve avere un valore preciso, contenuto in un determinato intervallo possibile; una velocità maggiore o minore, rispetto a tale intervallo, non permetterebbe al proiettile di rimanere in orbita.
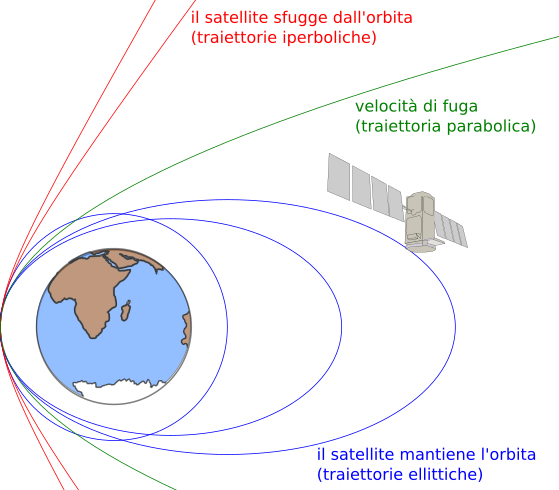
Le velocità ritenute possibili consentono al proiettile di compiere orbite paraboliche attorno alla superficie terrestre; inoltre, la minima velocità accettabile determina un orbita quasi circolare attorno alla Terra.
Con velocità minori il proiettile non riuscirebbe ad entrare in orbita, e ricadrebbe sulla sulla Terra.
Con velocità maggiori, invece, il proiettile sfuggirebbe all’attrazione gravitazionale, e la sua traiettoria è rappresentata da una curva iperbolica. Le traiettorie possibili iperboliche ed ellittiche sono infinite.
Vi è, inoltre, un caso particolare che è quello della velocità di fuga. La velocità di fuga è la velocità minima che permette ad un corpo di sfuggire all’attrazione gravitazionale, ed è tale che consente al corpo stesso di giungere a distanza infinita dal pianeta con la minima velocità, pressoché nulla.
Questa particolare velocità fa si che il corpo lasci l’orbita terrestre compiendo un moto rappresentato da una curva parabolica. A differenza delle altre curve, questa traiettoria è data da un solo valore preciso della velocità.
Velocità dei satelliti
Dato che il satellite ruota attorno ad un pianeta su un’orbita che possiamo considerare circolare, deve necessariamente essere presente una forza centripeta che gli permetta di rimanere in moto.
$ F = m * frac(v^2)(R + h) $
Con R indichiamo il raggio del pianeta, e con h la distanza del satellite dalla sua superficie.
Questa forza centripeta coincide proprio con la forza gravitazionale che il pianeta esercita sul satellite stesso.
$ F = G * frac(m*M)((R + h)^2) $
Possiamo, quindi, uguagliare le due scritture e ricavare così il valore della velocità del satellite:
$m * frac(v^2)(R + h) = G * frac(m*M)((R + h)^2) to v = sqrt(frac(G*M)(R + h))$
Notiamo che la massa del satellite non influisce sulla sua velocità, che diminuisce, invece, con l’aumentare della sua distanza dalla superficie del pianeta.
Il periodo di rivoluzione di un satellite
Il periodo di un satellite è il tempo che esso impiega a compiere un giro completo attorno al pianeta. Nel caso di un moto circolare, sappiamo che il periodo è dato dal rapporto 2πr/v. Anche in questo caso, possiamo applicare tale formula, ma alla velocità v sostituiamo la formula della velocità del satellite trovata precedentemente:
$T = frac(2π(R + h))(v) = frac(2π(R + h))(sqrt(frac(G*M)(R + h))) = 2π * frac((R + h)^(3/2))(sqrt(G*M)) $
I satelliti geostazionari
Un satellite geostazionario è un satellite che appare fermo ad un osservatore che si trova sulla superficie terrestre. Ciò significa, quindi, che il satellite ruota attorno alla Terra con lo stesso periodo terrestre, impiegando cioè un giorno a compiere un giro completo.
Questo tipo di satelliti sono molto utilizzati in campo metereologico o per le comunicazioni; essi si muovono su un’orbita che si trova nello stesso piano dell’equatore, ad una distanza di 35 800 km dalla superficie terrestre.
Potrebbero interessarti
Video lezioni: Le leggi di Keplero
Appunti: Le leggi di Keplero
Appunti: La gravitazione
Appunti: Dimostrazione delle leggi di Keplero
Appunti: Il campo gravitazionale
Appunti: Energia potenziale gravitazionale
