Il momento di una coppia di forze

Il momento di più forze

Se applichiamo su un corpo rigido più forze contemporaneamente, il momento totale delle forze è dato dalla somma dei singoli momenti di ciascuna forza.

Quindi, se le forze in questione sono $F_1, F_2, …, F_n$, e i rispettivi momenti $M_1, M_2, …, M_n$, il momento totale delle forze è dato da:

$ \vec M_(tot) = \vec M_1 + \vec M_2 + … + \vec M_n = \sum_[ k=1]^n \vec M_n $

Le coppie di forze

Su di un corpo possono agire più forze contemporaneamente; quando guidiamo un’automobile e giriamo il volante con entrambe le mani, le forze che agiscono sul volante sono due; si ha dunque una rotazione di esso.

In particolare, nel caso di due forze che hanno la stessa intensità, possono verificarsi due fenomeni; se le forze agiscono sulla stessa retta d’azione e hanno verso opposto, la risultante delle forze è nulla; quindi il corpo non trasla e non ruota, ma rimane fermo. Infatti, in questo caso, le due forze producono momenti che hanno stesso modulo, ma segno opposto; il momento totale delle forze è quindi nullo.

Altrimenti, se le due forze, che hanno la stessa intensità e verso opposto non hanno la stessa retta d’azione, allora esse producono una rotazione sul corpo su cui agiscono, come nel caso del volante. Infatti, in questo caso, il momento totale delle forze è diverso da zero, in quanto entrambe le forze producono un momento dello stesso segno, e che quindi fa ruotare il corpo nello stesso verso.

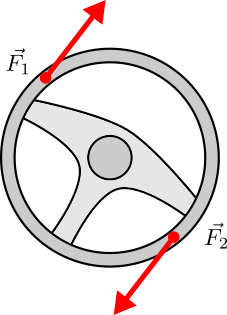
Coppia di forze

Una coppia di forze consiste in due forze $F_1$ e $ F_2$, di uguale intensità, ma opposte, applicate in due punti diversi di un corpo rigido.

Come nel caso di una singola forza, anche per la coppia di forze il momento descrive l’entità dell’effetto che la forza provoca sull’oggetto, in questo caso la rotazione; il momento di una coppia di forze si ottiene sommando i momenti delle singole forze calcolate rispetto ad uno stesso punto; esso dipende, quindi, dalle forze applicate e dalla loro distanza.

In particolare, il momento della coppia è indipendente dal particolare punto di applicazione.

Definiamo, inoltre, braccio della coppia la distanza tra le due rette d’azione delle forze; il momento della coppia, quindi, è un vettore che ha:

intensità uguale al prodotto dell’intensità di una delle forze e la lunghezza del braccio: $M = F ∙ b$;

direzione perpendicolare al piano che contiene le forze;

verso dato, anche in questo caso, dalla regola della mano destra, considerando, però, solo una delle due forze, e calcolando il momento rispetto al punto di applicazione dell’altra.

Regola della mano destra per una coppia di forze.

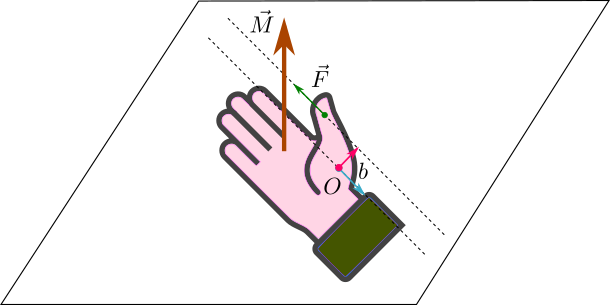
Senso di rotazione

Anche in questo caso, l’effetto della rotazione provocato dalle due forze può avvenire in senso orario o antiorario; ciò dipende dalla direzione in cui agiscono le forze.

Per convenzione, si considera positivo il momento che produce una rotazione antioraria; nel caso di una rotazione in senso orario, invece, il momento sarà negativo.

Può accadere che su uno stesso corpo rigido agiscano contemporaneamente due coppie di forze; se di queste coppie, una fa ruotare il corpo in senso orario (forze in blu), e l’altra in senso antiorario (forze in rosso), e se i momenti delle due coppie sono uguali, il corpo rimane fermo.

Tali coppie di forze si dicono quindi equivalenti.

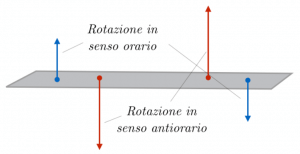
forze-e-rotazione — Rotazione prodotta da una coppia di forze.

Infatti, poiché le forze in rosso provocano una rotazione in senso antiorario, il momento relativo a tali coppie è positivo; mentre, il momento relativo alle forze il blu, che producono una rotazione in senso orario, sarà negativo.

Dato che i momenti delle coppie sono uguali (in valore assoluto), possiamo concludere che la loro somma, e quindi il momento totale, è uguale a zero; di conseguenza, non vi è rotazione del corpo.