Macchine semplici e leve - Matematicamente

Le macchine semplici

Molto spesso capita che la sola forza che esercitiamo su un corpo particolarmente grande o pesante rispetto a noi non sia sufficiente a far spostare, o a sollevare il corpo.

Per questo, si utilizzano dei macchinari appositi, detti macchine semplici; queste permettono di agire su un corpo applicando una forza al nostro posto, una forza molto più potente della nostra. Queste macchine sono, ad esempio, le leve o le carrucole.

Il loro funzionamento si basa sul fatto che la forza che viene applicata sul corpo (detta forza motrice) riesce ad equilibrare, e a vincere, un’altra forza di intensità o direzione diversa (detta forza resistente).

Infatti, nel caso della carrucola, la forza che si esercita sulla corda della stessa, che viene tirata verso il basso, permette di vincere la forza-peso dell’oggetto appeso al gancio, che quindi viene sollevato verso l’alto.

Il guadagno della macchina

Il rapporto tra la forza resistente e la forza motrice viene definito guadagno della macchina:

$ G = frac(F_r)(F_m)$

Si può notare, quindi, che se il guadagno della macchina è un valore elevato la macchina risulterà molto vantaggiosa; infatti la forza da applicare è molto più piccola rispetto alla forza resistente.

In particolare, una macchina viene definita vantaggiosa se il guadagno è maggiore di 1; altrimenti, se il guadagno è minore di 1, la macchina viene definita svantaggiosa.

Le leve

Le leve sono un particolare tipo di macchine semplici, presenti frequentemente nella vita quotidiana; esse permettono di aumentare o ridurre le forze.

Le leve sono formate da un corpo rigido, spesso un’asta, che può ruotare attorno ad un punto fisso, detto fulcro.

Chiamiamo la forza resistente e la forza motrice rispettivamente $F_r$ e $F_m$; le loro istanze dal fulcro si indicano con $b_r$ e $b_m$ (definiti bracci resistente e motore rispetto al fulcro).

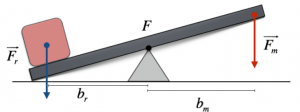
forza-resistente-motrice — Forza resistente e forza motrice in una leva di primo genere.

Nel caso in cui i momento delle forze che agiscono hanno stesso modulo, ma versi opposti, la leva è in equilibrio; quindi, in particolare, la somma dei momenti della forza resistente e di quella motrice è uguale a zero:

$F_r * b_r = F_m * b_m$

Possiamo anche affermare che una leva è in equilibrio se vale la seguente proporzione:

$F_m : F_r = b_r : b_m$

Molto spesso, non è necessario applicare una forza motrice molto grande, o comunque maggiore di quella resistente, per utilizzare la leva; infatti, l’esito dell’operazione dipende molto anche dalle lunghezze dei bracci delle forze in gioco.

Infatti, nel caso in cui la forza motrice è minore di quella resistente, sarà sufficiente utilizzare un braccio motore che sia maggiore di quello resistente.

Classificazione delle leve

La posizione del fulcro rispetto alle due forze, quindi, è molto importante; esso, infatti, influenza le lunghezze reciproche dei due bracci; in base a tale posizione, quindi, vengono classificate le leve:

se il fulcro di trova tra le due forze si hanno leve di primo genere, come sono ad esempio le forbici; se la forza motrice è minore di quella resistente, questo tipo di leva risulta vantaggiosa se il braccio motore è maggiore di quello resistente; sono svantaggiose altrimenti;

se la forza resistente si trova tra il fulcro e la forza motrice, si hanno leve di secondo genere; queste leve, come lo schiaccianoci, risultano sempre vantaggiose, qualunque siano le forze applicate, e qualunque sia la lunghezza die rispettivi bracci;

se la forza motrice si trova tra il fulcro e la forza resistente, si hanno leve di terzo genere; in questo caso, invece, le leve risultano sempre svantaggiose, quindi riducono le forze che vengono applicate su di esse;

Esempio:

Consideriamo una leva di terzo genere, in equilibrio sotto l’azione di una forza resistente di 5,7 N; sapendo che il braccio resistente misura 80 mm, e quello motore 55 mm, calcoliamo la forza motrice che equilibra la leva.

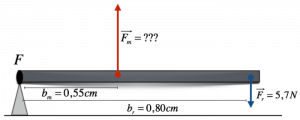
leva-terzo-genere — Forze agenti su una leva di terzo genere.

Sapendo che una leva (di qualsiasi tipo) è in equilibrio quando il momento della forza motrice è uguale a quello della forza resistente, possiamo applicare tale relazione per calcolare la forza resistente necessaria:

$F_r * b_r = F_m * b_m to F_m = frac (F_r * b_r)(b_m)$

ricordiamoci di esprimere le grandezze nella giusta unità di misura:

$F_r = 5,7 N $

$b_m = 55 mm = 0,55 cm$

$b_r = 80 mm = 0,80 cm$

Sostituendo troviamo, quindi:

$ F_m = frac (5,7 N * 0,80 cm ) (0,55 cm) = 8,3 N $