L'impulso di una forza - Matematicamente

L’impulso di una forza

Consideriamo una forza F che agisce su un corpo di massa m, provocando in esso un’accelerazione costante a.

Conoscendo il significato e la definizione della quantità di moto, possiamo scrivere il secondo principio della dinamica ( $ F = m*a $ ) in una nuova formulazione.

Scriviamo l’accelerazione come rapporto della variazione della velocità sulla variazione del tempo, e sostituiamo tale rapporto nella formula precedente:

$ vec a = frac (∆vec v)(∆t) to vec F = m * vec a = m * frac (∆vec v)(∆t) $

Moltiplichiamo ora entrambi i membri per la variazione di tempo ∆t:

$ vec F * ∆t = m * vec a * ∆t = m * frac (∆vec v)(∆t) * ∆t = m * ∆vec v$

Dalla precedente formula emerge una nuova grandezza, che prende il nome di impulso di una forza; l’impulso è dato dal prodotto della forza F per l’intervallo di tempo in cui essa agisce:

$ vec I = vec F * ∆t $

Da questa uguaglianza possiamo notare che la variazione di velocità di un oggetto di massa m non dipende solamente dalla forza che gli viene applicata, ma anche dalla durata di tale operazione.

Di conseguenza, se, per esempio, volessimo fermare un corpo in movimento, potremmo farlo in due modi diversi: applicando una forza elevata per un periodo di tempo breve, oppure una forza di intensità minore per un tempo maggiore.

Il teorema dell’impulso

Supponiamo che sotto l’azione della forza F il corpo passi dalla velocità $v_1$ alla velocità $v_2$; la variazione di velocità che esso subisce è data da $ ∆v = v_2 – v_1 $. Sostituiamo tale espressione nell’uguaglianza precedente:

$ vec F * ∆t = m * ∆vec v = m * (vec v_2 – vec v_1) = m * vec v_2 – m * vec v_1 = vec p_2 – vec p_1 = ∆ vec p $

L’uguaglianza che abbiamo ricavato prende il nome di teorema dell’impulso; esso afferma, quindi, che l’impulso di una forza applicata ad un corpo di massa m per un certo intervallo di tempo ∆t è uguale alla variazione della quantità di moto del corpo nello stesso intervallo di tempo.

Il teorema dell’impulso è particolarmente importante, e trova applicazione in molte situazioni e fenomeni naturali, come esplosioni, implosioni, che sono difficili da studiare. Infatti, spesso è molto difficile, se non impossibile, determinare con precisione le forze che agiscono, in quanto esse si applicano per tempi particolarmente brevi.

L’impulso di forze variabili

Il teorema dell’impulso può essere applicato se conosciamo il valore esatto di F, cioè se tale valore si mantiene costante nell’intervallo di tempo; se, invece, abbiamo a che fare con forze che possono variare in tale intervallo, si deve procedere diversamente.

In questo caso, infatti, potremmo suddividere l’intervallo ∆t in tanti piccoli sotto-intervalli, tali che in ciascuno di essi la forza si mantenga costante. L’impulso della forza F sarà dato, quindi, dalla somma degli impulsi delle forze in tutti gli intervalli.

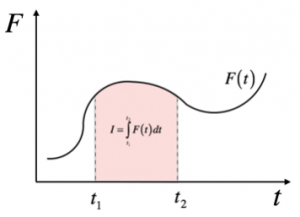
Se conosciamo l’espressione della forza in funzione del tempo, possiamo rappresentare l’andamento della forza in un grafico tempo-forza; in questo caso, potremmo calcolare facilmente il modulo dell’impulso, dato dall’area racchiusa tra il grafico della forza e l’asse t in un determinato intervallo di tempo (si calcola, cioè, l’integrale della forza in funzione del tempo, in un determinato intervallo).

forza-variabile — Il grafico tempo-forza rappresenta l’andamento di una forza variabile.

Esempio

Un’automobile di massa 800 kg si muove su un tratto di strada rettilineo; le forze che agiscono su di essa, acceleranti, o frenanti, dovute all’attrito, agiscono in funzione del tempo secondo il seguente andamento:

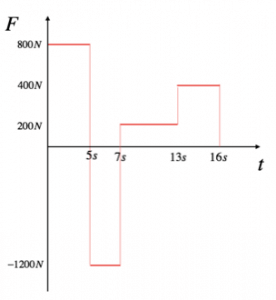
forze-variabili — Andamento delle forze che agiscono sul veicolo durante il percorso.

Calcolare quanto vale l’impulso totale della forza applicata all’automobile, e la variazione complessiva di velocità che essa subisce.

In questo caso abbiamo a che fare con una forza variabile nel tempo, di cui conosciamo l’andamento. Come possiamo vedere dal grafico, però, la forza si mantiene costante nei singoli tratti; possiamo, quindi, calcolare l’impulso totale della forza determinando l’impulso delle varie forze nei singoli tratti, e poi facendone la somma.

Nel primo tratto, si ha una forza F di 800 N per un intervallo di tempo di 5 s; l’impulso della forza è quindi:

$ I_1 = F_1 * ∆t_1 = 800 N * (5-0) s = 4000 N*s $

Nel secondo tratto la forza è negativa, e vale -1200N; essa viene applicata per due secondi; si ha quindi:

$ I_2 = F_2 * ∆t_2 = -1200 N * (7-5) s = -2400 N*s $

Applicando lo stesso ragionamento, otteniamo gli impulsi del terzo e del quarto tratto del percorso:

$ I_3 = F_3 * ∆t_3 = 200 N * (13-7) s = 1200 N*s $

$ I_4 = F_4 * ∆t_4 = 400 N * (16-13) s = 1200 N*s $

Calcoliamo l’impulso totale della forza sommando gli impulsi dei singoli tratti:

$ I_Tot = I_1 + I_2 + I_3 + I_4 = ( 4000 – 2400 + 1200 + 1200 ) N*s = 4000 N*s $

Per il teorema dell’impulso, l’impulso di una forza che agisce su un oggetto di massa m è uguale alla quantità di moto del corpo stesso; in questo caso, conoscendo il valore dell’impulso totale della forza, e conoscendo la massa dell’automobile, possiamo ricavare il valore della variazione di velocità:

$ vec I = vec F * ∆t = m * ∆vec v to ∆vec v = frac (vec I)(m) $

Sostituendo i valori numerici otteniamo:

$ ∆vec v = frac (vec I_Tot)(m) = frac (4000 N*s)(800 kg) = 5 m/s $