Le molle - Matematicamente

La forza elastica

Le molle sono strumenti di grande utilizzo, anche nella vita quotidiana, e ci permettono di svolgere numerose azioni. In fisica, per esempio, abbiamo visto l’utilizzo di una molla nel caso del dinamometro, che consente di determinare la forza-peso di un oggetto.

Una delle caratteristiche delle molle è il fatto che ogni volta che esse vengono deformate, cioè vengono compresse o allungate, e si altera così il loro stato di riposo, esse tendono a tornare nella posizione di equilibrio. Questo accade perché sulla molla agisce una forza propria di questo strumento, e perciò detta forza elastica.

Consideriamo una molla parallela al piano orizzontale, e fissata al muro; supponiamo di tirare la molla verso destra, allungandola rispetto alla posizione di riposo di una lunghezza $∆x$. La forza che stiamo imprimendo alla molla è, quindi, rivolta nella stessa direzione dello spostamento, verso destra. La forza elastica ha stessa direzione della nostra forza, ma verso opposto; infatti, la molla, cercando di tornare nella posizione di riposo, tenderà a spostarsi verso sinistra; la forza elastica, quindi, ha sempre verso opposto allo spostamento.

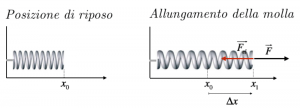
allungamento-molla — Allungamento della molla di una quantità ∆x rispetto alla posizione di riposo.

Consideriamo, ora, il caso in cui la molla venga compressa; la forza che stiamo applicando è ora rivolta verso verso sinistra, nella stesso verso dello spostamento $∆x$. La molla cercherà di tornare nella sua posizione di riposo, e quindi cercherà di allungarsi. La forza elastica agirà, quindi, verso destra, nella direzione opposta allo spostamento.

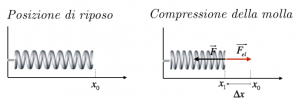
compressione-molla — Compressione della molla di una quantità ∆x rispetto alla posizione di riposo.

La forza elastica

Si può notare che il valore della forza elastica è direttamente proporzionale allo spostamento della molla rispetto alla posizione iniziale.

Infatti, la forza elastica può essere espressa mediante la legge di Hooke, per cui si ha:

$ vec F_(el) = -k * ∆ vec x $

dove $∆x$ rappresenta lo spostamento della molla, e k è una costante, detta costante elastica della molla. Il segno meno che compare nell’espressione sottolinea proprio il fatto che il vettore forza elastica ha verso opposto del vettore spostamento.

Questa legge vale solo nel caso di molle ideali e per deformazioni piccole; infatti, applicando forze particolarmente elevate la molla potrebbe reagire imprevedibilmente, o addirittura deformarsi essa stessa.

Il moto armonico della molla

Quando attacchiamo all’estremità di una molla (parallela al pavimento) una massa, ad esempio una pallina, e deformiamo la molla rispetto alla posizione di riposo, trascurando gli attriti presenti tra il pavimento e la massa, notiamo che la pallina comincerà a muoversi avanti e indietro, e subirà un’accelerazione da parte della molla.

In particolare, la forza cui è soggetta la pallina è uguale alla forza elastica della molla:

$ vec F_p = vec F_(el) to m * vec a = -k * vec s to m * vec a + k * vec s = 0 $

Dove con s indichiamo lo spostamento della molla dalla posizione di riposo.

Notiamo che questa equazione è molto simile all’equazione che descrive il moto armonico, che ricordiamo essere:

$ vec a = – \omega^2 * vec s to vec a + \omega^2 * vec s = 0 $

In effetti, la molla, oscillando avanti e indietro sotto l’azione della forza elastica, descrive proprio un moto armonico; l’equazione può anche essere scritta come segue:

$ vec a + frac (k)(m) * vec s = 0 $

Da questa scrittura, possiamo facilmente dedurre che la pulsazione è data da:

$ \omega^2 = frac (k)(m) to \omega = sqrt (frac (k)(m)) $

Poiché il periodo dell’oscillazione è dato dal rapporto tra 2π e la pulsazione, otteniamo:

$ T = frac (2π)(\omega) = 2π * sqrt( frac (k)(m) )$

Esercizio

Consideriamo una molla posta a terra, e ancorata al terreno su un estremo. All’altro estremo della molla è attaccata una sfera, che viene fatta ruotare sul piano orizzontale. La sfera descrive, così, un moto circolare uniforme. Sapendo che la massa della sfera è di 0.21 kg, che la costante elastica della molla misura 289 N/m, che il raggio della circonferenza che percorre la sfera è di 0,381 m e che essa si muove con velocità angolare pari a 3,21 rad/s, determiniamo la lunghezza della molla a riposo.

La sfera che si muove di moto circolare uniforme è sottoposta alla forza centripeta dovuta a tale moto; questa forza è uguale alla forza elastica della molla. Da questa uguaglianza possiamo facilmente ricavare l’entità dell’allungamento della molla:

$F_c = F_(el) to m * \omega^2 * r = k * s to s = frac ( m * \omega^2 * r)(k) $

Di conseguenza, la lunghezza della molla a riposo è data dalla differenza tra il raggio della circonferenza e l’entità dell’allungamento:

$ l = r – s = r – frac ( m * \omega^2 * r)(k) $

Sostituendo i valori numerici abbiamo:

$ l = 0,381 – frac ( 0,21 kg * (3,21 (rad)/s )^2 * 0,381 m)(289 N/m) = $

$= 0,381 m – 0,00285 m = 0,378 m $