Gli effetti dei corpi in movimento
Come sappiamo, gli oggetti in movimento sono in grado di produrre degli effetti (compiendo un lavoro) su altri oggetti, che magari sono fermi.
Consideriamo due sfere in movimento, che urtano contro una superficie.
A parità di velocità, se le sfere hanno massa diversa (m e M), quella di esse con massa maggiore (M) urterà la superficie con una forza maggiore; lo stesso accade se le due sfere hanno massa uguale, ma si muovono con velocità diverse (v e V); la sfera che si muove a velocità maggiore (V) colpirà la superficie con una forza maggiore.
Cosa accade, però, se le sfere hanno sia massa che velocità diverse?
Può accadere che, se la sfera con massa minore (m) si muove molto velocemente, con velocità V, e quella con massa maggiore (M) si muove più lentamente, con velocità v, colpendo la superficie producano lo stesso effetto. Può accadere, cioè, che esse urtino la superficie con la stessa forza.
La quantità di moto
Gli effetti prodotti da un corpo in movimento, quindi, dipendono sia dalla velocità con cui esso si sta muovendo, sia dalla sua massa.
Per questo è utile introdurre una nuova grandezza, definita quantità di moto, espressa come il prodotto della massa del corpo per la sua velocità:
$ vec p = m * vec v $
La quantità di moto è un vettore che ha la stessa direzione e lo stesso verso del vettore velocità; il suo modulo è direttamente proporzionale sia alla velocità del corpo che alla sua massa.
Legge di conservazione della quantità di moto
In un sistema dove non agiscono forze esterne, la quantità di moto totale del sistema si conserva.
Questa legge vale se si considera la quantità di moto presente all’interno del sistema generale, non la quantità di moto di un singolo elemento. Infatti, può accadere che in due istanti diversi un determinato oggetto abbia quantità di moto differenti, in quanto, ad esempio, esso può subire una variazione di velocità.
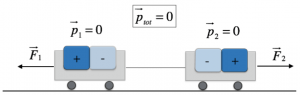
Consideriamo, per esempio, due carrelli della stessa massa collegati con una fune, sopra ai quali sono poste due calamite orientate in modo da avere i poli dello stesso segno vicini. I carrelli tendono, quindi, a respingersi, e per questo la fune è in tensione.
Poiché i carrelli sono fermi, la loro quantità di moto iniziale è nulla; anche la quantità di moto dell’intero sistema (cioè dei due carrelli considerati insieme) è, quindi, nulla.
Se, però, la fune che unisce i carrelli viene tagliata, essi, respingendosi, tenderanno a muoversi in direzioni opposte, acquistando, quindi, velocità. La quantità di moto è un vettore che ha la stessa direzione e lo stesso verso del vettore velocità; di conseguenza, poiché i carrelli si muovono in versi opposti, tali saranno anche i vettori quantità di moto; i vettori velocità dei carrelli, infatti, hanno stessa direzione e verso opposto.
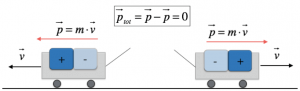
Notiamo, quindi, che la quantità di moto dei singoli carrelli è variata nelle due situazioni; la quantità di moto dell’intero sistema, invece, è rimasta uguale. I vettori quantità di moto, infatti, hanno stesso modulo, stessa direzione ma verso opposto, e quindi si annullano.
Esercizio
Consideriamo due automobili che si muovono in direzioni tra loro perpendicolari; sapendo che la massa delle automobili è di 1500 kg, e che esse si muovono alla velocità di 120 km/h, calcoliamo:
- il valore della quantità di moto di ciascuna di esse;
- il valore della quantità di moto totale delle due auto.
Per calcolare il modulo della quantità di moto di ciascuna auto, possiamo semplicemente applicare la definizione di quantità di moto; calcoliamo, quindi, il prodotto della massa per la velocità.
Ricordiamoci, però, di esprimere de grandezze nelle giuste unità di misura:
$ v = 120 km/h = frac (120)(3,6) m/s = 33,33 m/s $
La quantità di moto delle auto è quindi:
$ | vec p | = m * | vec v| = 1500 kg * 33,33 m/s = 50000 kg *m/s = 5,5 * 10^4 kg * m/s $
Per calcolare la quantità di moto totale del sistema dobbiamo effettuare la somma vettoriale dei vettori quantità di moto delle singole auto.
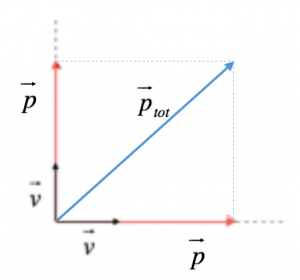
Poiché i vettori sono tra loro perpendicolari, la quantità di moto totale è data da:
$ | vec p_Tot | = sqrt (| vec p_1 |^2 + | vec p_2 |^2) = sqrt (2 | vec p_1 |^2 ) = $
$ sqrt (2 * (5,5 * 10^4 kg * m/s)^2 ) = 7,70 * 10^4 kg * m/s $
Potrebbero Interessarti
Video Lezioni: La dinamica
Video Lezioni: L’energia
Video Lezioni: La dinamica dei sistemi
Video Lezioni: Gli urti
Appunti: Le Forze
Appunti: Le forze di contatto: l’attrito
Appunti: Le forze a distanza: Forze fondamentali
Appunti: Corpi in equilibrio
Appunti: Il momento di una forza
Appunti: Il momento di una coppia di forze
Appunti: Forze che agiscono su un corpo rigido
Appunti: L’equilibrio di un corpo rigido
Appunti: Il primo principio della dinamica
Appunti: Effetto delle forze sui corpi rigidi, e secondo principio della dinamica
Appunti: Il terzo principio della dinamica
Appunti: La discesa lungo un piano inclinato
Appunti: Il lavoro
Appunti: L’energia cinetica
Appunti: Forze conservative e dissipative, energia potenziale.
Appunti: Energia potenziale gravitazionale e energia potenziale elastica
Appunti: Energia meccanica
Appunti: L’impulso di una forza
Appunti: Gli urti
Appunti: Il centro di massa
Appunti: Il momento angolare
Appunti: Il momento di inerzia
