Il pendolo semplice - Matematicamente

Il pendolo semplice: equilibrio e moto armonico

Il pendolo è uno strumento costituito da una sferetta di massa m attaccata ad una superficie orizzontale rigida per mezzo di un filo, o un’asta, inestensibile e di massa trascurabile.

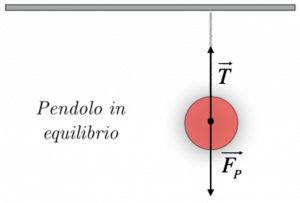
Quando la massa si trova lungo la verticale rispetto al piano, il pendolo è in una posizione di equilibrio. Infatti, le forze che agiscono sulla sfera sono solamente la forza peso relativa alla sua massa, e la tensione della fune; queste sono uguali in modulo, e hanno verso opposto, quindi si bilanciano; per questo, la sfera è ferma in una posizione di equilibrio.

pendolo-equilibrio — Il pendolo è in equilibrio quando la tensione della fune e la forza peso sono uguali e contrarie, cioè quando si bilanciano.

Se, però, prendiamo la sfera e la spostiamo dalla posizione iniziale di equilibrio, e la lasciamo andare, questa comincerà ad oscillare; nel caso in cui gli attriti che si generano, dovuti all’aria e allo sfregamento nel punto in cui è attaccato il filo, siano trascurabili, la sfera continuerebbe ad oscillare con un’oscillazione praticamente costante.

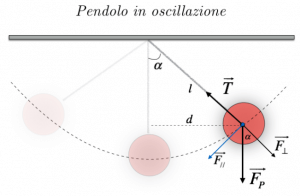
pendolo-oscillazione — Il pendolo oscilla in modo costante: la forza che influenza l’oscillazione è la componente parallela della forza-peso.

Inoltre, possiamo notare che anche il pendolo descrive un moto armonico, dovuto alla massa della pallina e alla sua forza-peso.

Scomponiamo la forza-peso della pallina nelle sue componenti: $F_//$ che ha direzione tangente alla traiettoria descritta dalla pallina, e $F_⊥$ che, invece, da direzione perpendicolare ad essa; notiamo che la tensione della fune è bilanciata dalla componente perpendicolare della forza-peso. Il moto della pallina, quindi, dipende da $F_//$, che, anche in questo caso, come per la forza elastica, ha verso contrario a quello dello spostamento. Infatti, tale forza agisce contro il moto della pallina, e tende a riportarla nella posizione di equilibrio.

Questa caratteristica della forza che agisce sulla pallina nel caso del pendolo, è in accordo con il fatto che anche per il pendolo si può parlare di moto armonico.

Possiamo, infatti, mostrare che anche in questo caso si può determinare un’equazione del moto che rispecchia quella del moto armonico.

Indichiamo con $\alpha\$ l’angolo che si forma tra la fune e la verticale; la componente della forza-peso tangente alla traiettoria si ottiene in questo modo:

$F_⊥ = F_P * sin (\alpha) = m * g * frac(d)(l)$

Possiamo approssimare con d la lunghezza dell’arco di traiettoria corrispondente nel caso in cui le oscillazioni siano piccole.

Indichiamo con s il vettore spostamento, e sapendo che la forza tangente ha direzione opposta a tale vettore, possiamo scrivere:

$vec F_⊥ = -frac(m * g) (l) * vec s$

Poiché tale forza imprime un’accelerazione alla pallina, abbiamo la relazione $F = m*a$, dal secondo principio della dinamica. Uguagliando le due espressioni, otteniamo l’equazione cercata:

$vec F_⊥ = -frac(m * g) (l) * vec s $ ; $vec F_⊥ = m * vec a to $

$ -frac(m * g) (l) * vec s = m * vec a to m * l * vec a + m * g * vec s = 0$

Il periodo di oscillazione

Una caratteristica molto importante del pendolo, che ha permesso ai fisici di costruire orologi basati sulla sua oscillazione, riguarda la durata delle oscillazioni, e quindi il periodo.

Il periodo del pendolo può essere calcolato mediante la seguente formula:

$ T = 2π * sqrt frac (l)(g) $

dove con l si indica la lunghezza del filo, e con g l’accelerazione di gravità.

Come possiamo notare, il periodo di oscillazione del pendolo non dipende in alcun modo dall’angolo di oscillazione, cioè dall’ampiezza dell’oscillazione, o dalla distanza (d) dalla posizione di riposo.

Questo significa che, quando con il passare del tempo, a causa degli attriti con l’aria, le oscillazioni diventano sempre più piccole, passando da un angolo iniziale γ a un angolo successivo γ’, il tempo impiegato dalla pallina per spaziare il secondo angolo sarà esattamente uguale a quello impiegato per spaziare il primo.

Isocronia del pendolo — Il tempo impiegato per spaziare il primo angolo è uguale al tempo impiegato per spaziare il secondo

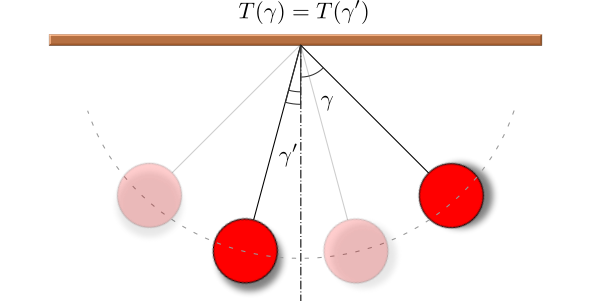
Questa particolare proprietà è detta isocronia; grazie ad essa è possibile sfruttare il meccanismo del pendolo per costruire gli orologi.

Esempio:

Calcoliamo il periodo di oscillazione di un pendolo, sapendo che la lunghezza del filo è di 51 cm, e che alla sua estremità è attizzata una massa di 43 g (ci troviamo sulla Terra).

Per determinare il periodo di oscillazione del pendolo utilizziamo la formula vista precedentemente; ricordiamo che le grandezze devono essere espresse nelle giuste unità di misura:

$ 51 cm = 0,51 m $

$ T = 2π * sqrt frac (l)(g) = 2π * sqrt frac (0,51 m)(9,81 m/s^2) = 1,4 s $

Notiamo che il problema ci ha fornito un dato superfluo: il periodo di oscillazione, infatti, è indipendente dalla massa appesa al filo.