Il momento di una forza

Il momento: introduzione

Nel caso di un corpo rigido, a differenza del punto materiale, non possiamo considerare solo i moti traslazionali, cioè le traslazioni; si devono tenere presenti alcune proprietà dei corpi rigidi.

Infatti, essendo un corpo esteso, e non un punto, il corpo rigido può subire l’effetto di una forza in qualunque punto della sua estensione; ciò può provocare effetti diversi.

Inoltre, i possibili moti che esso può subire sono differenti:

il moto di traslazione comporta uno spostamento senza che vi sia un cambiamento dell’orientazione nello spazio dell’oggetto; quando subisce questo moto, tutti i punti del corpo rigido si spostano percorrendo la stessa distanza su traiettoria rettilinee; (questo moto si verifica, ad esempio, quando trasciniamo un oggetto);

il moto di rotazione invece fa ruotare l’oggetto senza che esso si sposti dalla posizione iniziale; in questo caso, i punti del corpo rigido percorrono archi di circonferenze concentriche (questo moto si verifica, ad esempio, quando svitiamo un bullone con una chiave inglese).

I due moti, poi, possono anche presentarsi insieme.

Il moto di rotazione

Il moto di rotazione è quello che si ha, ad esempio, quando applichiamo una forza su di una chiave inglese per svitare un bullone; notiamo che agendo con una chiave più lunga lo sforzo da compiere è minore, poiché il bullone ruota più facilmente.

Ciò accade perché l’effetto della rotazione non dipende esclusivamente dalla forza che applichiamo e dalla sua intensità; essa dipende anche dal punto di applicazione e dalla direzione della forza.

Si definisce braccio di una forza F rispetto ad un punto O la distanza tra il punto O e la retta su cui giace F.

In particolare, se chiamiamo r il vettore posizione del punto O rispetto a F, il braccio è dato dalla componente perpendicolare di tale vettore:

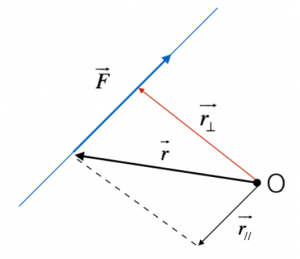
braccio-forza — Braccio di una forza F rispetto ad un punto O.

Il momento di una forza è un vettore che esprime l’effetto di rotazione causato dalla forza stessa. In particolare, il vettore ha le seguenti caratteristiche:

il suo modulo è dato dal prodotto dell’intensità della forza F e il modulo del braccio: $M = F ∙ b$;
la sua unità di misura nel Sistema Internazionale è, quindi, Newton per metro ($N ∙ m$);
la sua direzione è perpendicolare al piano che contiene il vettore forza e il punto O;

il suo verso è dato dalla regola della mano destra: si posizione il pollice sulla congiungente il punto O e il punto di applicazione della forza, e le altre dita nella direzione di F; il verso del momento è quello uscente dal palmo della mano.

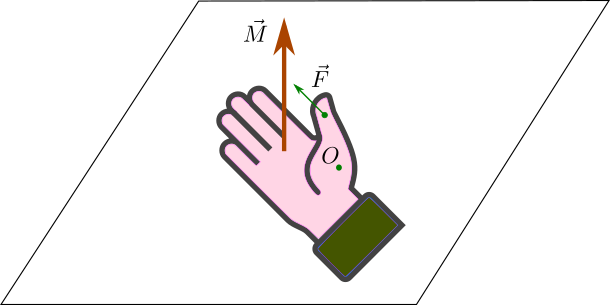
Poiché il momento di una forza è un vettore, le sue proprietà possono essere più semplicemente riassunte dicendo che il momento è uguale al prodotto vettoriale del vettore posizione r e il vettore forza F:

$ \vec M = \vec r xx \vec F $

Si spiega, quindi, come mai per svitare un bullone con una chiave inglese, e per faticare meno si seguono alcune accortezze; si può applicare una forza molto intensa, o utilizzare uno strumento molto lungo; il momento, infatti, è direttamente proporzionale sia alla forza che al braccio.

Se indichiamo con $\alpha$ l’angolo tra i vettori r ed F, possiamo esprimere il loro prodotto vettoriale nel seguente modo:

$ \vec M = \vec r xx \vec F = r * F * sin\alpha$

Il momento di una forza può essere positivo, negativo o nullo in base al senso di rotazione del braccio. Se il senso è quello orario, il momento viene considerato negativo; se il senso di rotazione è antiorario si avrà un momento positivo.

Se, invece, non vi è rotazione, il momento è nullo.