Il concetto di lavoro
Il concetto di lavoro è strettamente collegato a quello di forza e di spostamento. Quando, infatti, solleviamo una cassa e la trasportiamo per un certo tratto, abbiamo compiuto un lavoro.
Inoltre, questa nuova grandezza è strettamente collegata con il concetto di energia. Tutte le volte, infatti, che abbiamo compiuto un lavoro su un corpo, questo corpo ha acquisito a sua volta la capacità di compiere un lavoro.
Ad esempio, se compiamo un lavoro mettendo in moto un carrello, esso potrà urtare un oggetto fermo mettendolo in moto a sua volta. Si dice, quindi, che il carrello ha acquisito energia. L’energia, poi, può essere di tipo diverso, a seconda del corpo che stiamo considerando; nel caso del carrello, si parla di energia di movimento. Se consideriamo una cassa che viene sollevata, essa possederà un’energia di posizione; facendola cadere, infatti, la forza-peso compie un lavoro positivo.
Definizione di lavoro
Diamo una definizione di lavoro di una forza F come il prodotto scalare della forza per lo spostamento rispetto al punto di applicazione:
$ L = vec F * vec s = L * s * cos (Θ) $
dove con θ si indica l’angolo compreso tra i vettori forza e spostamento
Il lavoro di una forza, quindi, dipende dall’angolo compreso tra il vettore forza e il vettore spostamento; di conseguenza, in base alla posizione di essi, potremmo avere un lavoro positivo, negativo o nullo.
Consideriamo il caso in cui il vettore forza e il vettore spostamento siano paralleli; ciò accade, ad esempio, quando spingiamo in avanti un carrello:
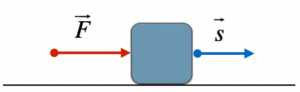
In questo caso, l’angolo compreso tra tali vettori è 0; possiamo calcolare il lavoro compiuto semplicemente come prodotto del modulo della forza per l’entità dello spostamento, essendo il coseno di 0 uguale a 1:
$ L = vec F * vec s = L * s * cos (Θ) =L * s * cos (0°) =L * s $
Lavoro motore e lavoro resistente
Il lavoro che si compie sotto le ipotesi precedenti serve, quindi, per compiere determinate azioni; ad esempio per mettere in moto un corpo fermo, o mantenere in movimento un corpo che si sta già muovendo; per questo prende il nome di lavoro motore.
In particolare, si può definire l’unità di misura del lavoro, cioè il Joule (J), come il lavoro compiuto da una forza di 1N quando questa provoca lo spostamento di un metro dal punto di applicazione: 1 J = 1 N ⋅1 m.
Consideriamo, ora, il caso in cui il vettore forza e il vettore spostamento siano opposti; ciò accade, ad esempio, quando cerchiamo di rallentare, o di fermare, un oggetto in movimento:
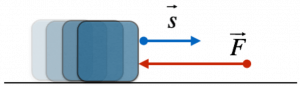
In questo caso l’angolo compreso tra i due vettori è di 180°; poiché il coseno di tale angolo è -1, il valore del lavoro sarà negativo, e dato da:
$ L = vec F * vec s = L * s * cos (Θ) =L * s * cos (180°) = – L * s $
La forza applicata al corpo, quindi, si oppone al suo spostamento; il lavoro che ne deriva viene detto lavoro resistente.
Nel caso, invece, in cui il vettore forza e il vettore spostamento siano perpendicolari, per esempio nel caso della forza-peso che agisce su una valigetta che stiamo trasportando, l’angolo compreso tra i vettori è di 90°.
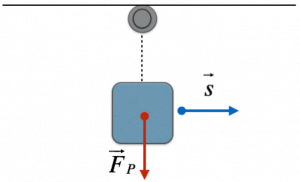
Poiché il coseno di 90° è zero, il lavoro risulterà nullo.
$ L = vec F * vec s = L * s * cos (Θ) =L * s * cos (90°) = 0 $
In questo caso, quindi, la forza peso non influenza in alcun modo lo spostamento del corpo, e non compie lavoro.
Il lavoro compiuto da più forze
Se vi sono due o più forza che agiscono contemporaneamente su un corpo che si sposta, può capitare che solo alcune di esse compiano lavoro.
In particolare, possiamo calcolare il lavoro totale generato dalle forze sul corpo in due modi.
- Calcolando il lavoro eseguito da ogni singola forza sul corpo, e poi sommare algebricamente i lavori ottenuti;
- calcolando la risultante delle forze che agiscono, e successivamente il lavoro che compie la risultante.
Potrebbero Interessarti
Video Lezioni: La dinamica
Video Lezioni: L’energia
Video Lezioni: La dinamica dei sistemi
Video Lezioni: Gli urti
Appunti: Le Forze
Appunti: Le forze di contatto: l’attrito
Appunti: Le forze a distanza: Forze fondamentali
Appunti: Corpi in equilibrio
Appunti: Il momento di una forza
Appunti: Il momento di una coppia di forze
Appunti: Forze che agiscono su un corpo rigido
Appunti: L’equilibrio di un corpo rigido
Appunti: Il primo principio della dinamica
Appunti: Effetto delle forze sui corpi rigidi, e secondo principio della dinamica
Appunti: Il terzo principio della dinamica
Appunti: La discesa lungo un piano inclinato
Appunti: La potenza
Appunti: L’energia cinetica
Appunti: Forze conservative e dissipative, energia potenziale.
Appunti: Energia potenziale gravitazionale e energia potenziale elastica
Appunti: Energia meccanica
Appunti: La quantità di moto
Appunti: L’impulso di una forza
Appunti: Gli urti
Appunti: Il centro di massa
Appunti: Il momento angolare
Appunti: Il momento di inerzia
