Il centro di massa

Consideriamo un sistema di punti materiali; possiamo definire un punto geometrico particolare, che prende il nome di centro di massa. Il centro di massa ha proprietà differenti in base al sistema in cui si trova.

Consideriamo il caso generale, in cui abbiamo n punti di masse $m_1, m_2, …, m_n$, che in un riferimento stabilito si trovano nelle posizioni di coordinate $x_1, x_2, …, x_n$.

Ipotizziamo che le particelle si muovano in un piano; per determinare la loro posizione è necessario conoscere l’ascissa e l’ordinata dei punti che, nel piano, le rappresentano.

L’ascissa $x_cm$ del punto che rappresenta il centro di massa è data dalla seguente formula:

$ x_cm = frac (m_1*x_1 + m_2*x_2 + … + m_n*x_n)(m_1 + m_2 + … + m_n) $

Similmente, l’ordinata di tale punto può essere ottenuta nel seguente modo:

$ y_cm = frac (m_1*y_1 + m_2*y_2 + … + m_n*y_n)(m_1 + m_2 + … + m_n) $

Se il punto materiale non si muove semplicemente in un piano, ma si muove in uno spazio tridimensionale, occorre introdurre anche una terza coordinata z; tale coordinata, riferita al punto materiale in questione, si ottiene con una formula analoga alle precedenti:

$ z_cm = frac (m_1*z_1 + m_2*z_2 + …+ m_n*z_n)(m_1 + m_2 + … + m_n) $

Esempio

Consideriamo il caso semplice in cui si hanno due particelle che si muovono lungo una retta; per determinare la posizione del centro di massa ci occorre conoscere soltanto la sua ascissa.

Applicando la formula precedente al caso di due soli punti, troviamo che tale ascissa è data da:

$ x_cm = frac (m_1*x_1 + m_2*x_2 )(m_1 + m_2 ) $

E, in particolare, se le due particelle avessero la stessa massa, l’ascissa del punto materiale si otterrebbe come ascissa di un punto medio tra tali punti:

$ x_cm = frac (x_1 + x_2 )(2 ) $

Quindi, se le due particelle hanno la stessa massa, il centro di massa è equidistante da entrambi, cioè si trova nel punto medio del segmento che li congiunge.

Altrimenti, se i punti hanno masse diverse, il centro di massa risulta più vicino alla particella di massa maggiore.

Moto descritto dal centro di massa

Il concetto di centro di massa ci permette di analizzare il moto di alcuni oggetti e di alcuni corpi che altrimenti sarebbe molto complesso da studiare. Infatti, anche se l’oggetto in questione si sta muovendo apparentemente in maniera casuale, è possibile che il suo centro di massa stia compiendo, in realtà, un moto uniforme.

Può essere dimostrato, infatti, che nel caso di un sistema fisico isolato, nel quale vale la conservazione della quantità di moto, il centro di massa si muove di moto rettilineo uniforme.

Ciò accede, ad esempio, nel caso in cui si spinge un corpo rigido, come una sbarretta di metallo, lungo una superficie piana: la sbarretta compie due moti, uno di traslazione, e l’altro di rotazione, ma il suo centro di massa si muove di moto rettilineo uniforme.

Esaminiamo, ora, il caso in cui il sistema fisico non sia isolato: in questo caso, non vale la conservazione della quantità di moto. Il moto del centro di massa dipende sia dalla risultante delle forze esterne che agiscono sul corpo, sia dalla massa totale del corpo stesso. Infatti, incentro di massa si muoverà proprio come un punto materiale che possiede tutta la massa del corpo, e su cui agisce una forza pari alla risultante delle forze che agiscono sull’oggetto stesso.

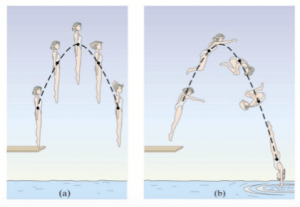
Questo tipo di moto può essere descritto, ad esempio, dal centro di massa di un tuffatore che si lancia da un trampolino: in questo caso, il centro di massa descrive un moto parabolico.

moto-centro-di-massa — Il centro di massa di corpi rigidi descrive sempre un moto uniforme; in questo caso, il centro di massa del tuffatore descrive un moto parabolico.

Il caso dei sistemi fisici non isolati trova riscontro anche nel teorema dell’impulso; in questo caso, però, questo viene applicato ad un corpo esteso, invece che ad un solo punto materiale.

Quando abbiamo a che fare con un sistema di punti che interagiscono tra loro, dobbiamo tener presente che su di essi agiscono sia forze esterne che forze interne al sistema, dovute appunto alle interazioni tre i punti. Tuttavia, per il principio di azione e reazione, le forze interne al sistema sono opposte a due a due, e la loro risultante è quindi nulla. Il moto dei punti, dunque, dipende solo dalle forze esterne; possiamo quindi utilizzare la seguente formula per la quantità di moto:

$ ∆ vec p_Tot = vec F_Tot * ∆t $