Gli urti - Matematicamente

Gli urti su una retta

Consideriamo due sfere che si muovono in linea retta, nella stessa direzione, ma in versi opposti, cioè avvicinandosi l’una verso l’altra.

Il moto delle palline, nella situazione reale, è influenzato da molti fattori, e forze esterne, come la forza di attrito radente con la superficie, la forza di attrito viscoso con l’aria, ecc…

Quando, però, le palline si scontrano, la forza risultante dall’urto è talmente grande che, anche se avviene in un lasso di tempo notevolmente piccolo, è tale da rendere trascurabili tutte le altre forze.

Di conseguenza, le forze di interazione tra le palline, cioè le forze interne al sistema pallina-pallina, rendono trascurabili quelle esterne.

Possiamo, quindi, affermare che quando vi è un urto tra due oggetti, essi si comportano come se fossero un sistema fisico isolato, e di conseguenza, la loro quantità di moto totale si conserva.

Se, inizialmente, le palline di masse $m_1$ e $m_2$ si muovono a velocità $v_1$ e $v_2$, e dopo l’urto le loro velocità risultano $V_1$ e $V_2$, la conservazione della quantità di moto è data da:

$ vec p_Tot(i) = vec p_Tot(f) to m_1 * vec v_1 + m_2 * vec v_2 = m_1 * vec V_1 + m_2 * vec V_2 $

Gli urti elastici

Nel caso degli urti elastici, oltre alla conservazione della quantità di moto si ha anche la conservazione dell’energia cinetica totale dei corpi che interagiscono.

Questi urti avvengono, solitamente, quando un oggetto in movimento ne colpisce un’altro che è fermo, mettendolo così in moto. Il primo oggetto, dopo l’urto, si ferma.

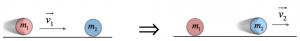
In questo caso, quindi, abbiamo due equazioni che descrivono il moto dei corpi, una riguardane la conservazione dell’energia cinetica, l’altra quella della quantità di moto:

$ \{ (p_Tot(i) = p_Tot(f) ), (k_Tot(i) = k_Tot(f)) :}$

$ \{ ( m_1 * v_1 + m_2 * v_2 = m_1 * V_1 + m_2 * V_2 ), ( 1/2*m_1*(v_1)^2 + 1/2*m_2*(v_2)^2 = 1/2*m_1*(V_1)^2 + 1/2*m_2*(V_2)^2) :}$

Questo sistema ci permette, conoscendo le masse dei corpi e le loro velocità iniziali, di ricavare le loro velocità finali.

Gli urti anelastici

Gli urti anelastici avvengono tra due corpi, di cui uno è in movimento e l’altro è fermo. A differenza degli urti elastici, però, dopo lo scontro il primo oggetto non si ferma, ma continua il suo moto insieme al secondo.

In questo caso, la velocità finale dei corpi dopo l’urto dipende esclusivamente dalla conservazione della quantità di moto dei corpi stessi.

Infatti, dato che dopo l’urto i due oggetti si muoveranno insieme, la loro velocità finale sarà uguale, quindi non avremmo bisogno di altre equazioni per determinarla, oltre a quella della conservazione della quantità di moto:

$ m_1 * v_1 + m_2 * v_2 = m_1 * V_1 + m_2 * V_2 = ( m_1 + m_2 ) * V to $

$ V = frac (m_1 * v_1 + m_2 * v_2)(m_1 + m_2 ) $

Gli urti obliqui

Nel caso di urti che non avvengono tra due oggetti che si muovono in linea retta è molto più difficile studiare il loro moto in seguito all’urto; esso infatti è influenzato da diversi fattori, tra cui la forma degli oggetti, le loro dimensioni, ecc..

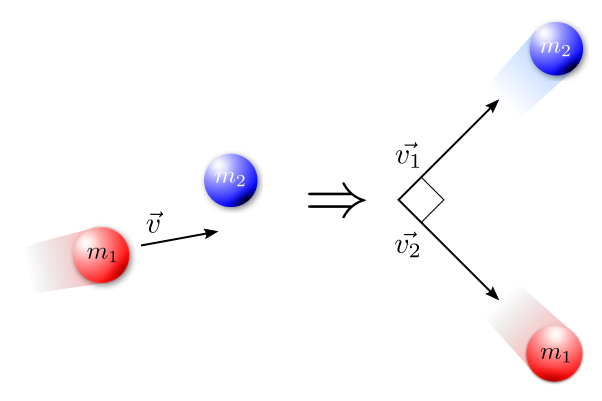
Il caso più semplice è quello in cui gli oggetti in questione sono due biglie di massa uguale; una di esse è in moto, mentre l’altra è ferma; la biglia in movimento urta la seconda in modo elastico.

Si può dimostrare che, in questo caso, dopo l’urto le due biglie si muoveranno con velocità perpendicolari tra loro.

Urto tra due biglie, di cui una in stato di quiete — Negli urti obliqui, un corpo in movimento ne urta un secondo inizialmente fermo; in seguito all’urto, i due corpi si muoveranno entrambi, e le loro velocità saranno perpendicolari

Esercizio

Due biglie identiche si trovano su un piano orizzontale. La prima biglia, in movimento, colpisce elasticamente la seconda biglia, che è inizialmente ferma. In seguito all’urto, le due biglie si muovono alle velocità, rispettivamente, di 2,5 m/s e 4,2 m/s.

Determinare il valore della velocità della biglia in movimento prima dell’urto.

Dai dati che fornisce il problema, conosciamo il valore delle velocità finali delle biglie in seguito all’urto.

L’urto in questione è un urto elastico; sappiamo quindi che in esso si conserva sia la quantità di moto del sistema, sia l’energia cinetica complessiva. Possiamo, quindi, impostare un sistema del tipo:

$ \{ ( m_1 * v_1 + m_2 * v_2 = m_1 * V_1 + m_2 * V_2 ), ( 1/2*m_1*(v_1)^2 + 1/2*m_2*(v_2)^2 = 1/2*m_1*(V_1)^2 + 1/2*m_2*(V_2)^2) :}$

Sappiamo che le biglie sono identiche, quindi in particolare hanno anche la stessa massa; possiamo, quindi, semplificare le masse e otteniamo:

$ \{ ( v_1 + v_2 = V_1 + V_2 ), ( (v_1)^2 + (v_2)^2 = (V_1)^2 + (V_2)^2) :}$

Sappiamo, inoltre, che la seconda biglia è inizialmente ferma, quindi che la sua velocità è nulla: v2 = 0:

$ \{ ( v_1 = V_1 + V_2 ), ( (v_1)^2 = (V_1)^2 + (V_2)^2) :}$

Notiamo che la prima equazione del sistema è un’equazione vettoriale; essa ci dice che la velocità iniziale della prima biglia è data dalla somma vettoriale dei vettori velocità finale delle biglie dopo l’urto.

Poiché tali vettori velocità formano un angolo di 90° dopo l’urto, l’espressione del modulo di $v_1$ è data proprio dalla seconda equazione:

$ v_1 = sqrt ((V_1)^2 + (V_2)^2) = sqrt ((2,5)^2 + (4,2)^2) = 4,89 m/s $