Forze conservative e dissipative, energia potenziale.

Forze conservative e dissipative

Le forze possono essere suddivise in due categorie, quelle conservative e quelle dissipative.

Le prime, sono forze per le quali il lavoro compiuto dipende solo dalla posizione iniziale e da quella finale, e non dal particolare tragitto che viene effettuato durante lo spostamento.

Se una forza non è conservativa, allora essa si dice dissipativa.

Esempio di forza conservativa

La forza-peso è un esempio di forza conservativa.

Cerchiamo di capire questo concetto esaminando il valore del lavoro che compie la forza peso durante la discesa di una biglia in due diverse circostanze: nel primo caso lungo un piano inclinato, e nel secondo lungo una scalinata.

Consideriamo un piano inclinato di altezza h e di lunghezza l, e una biglia che si trova in cima ad esso.

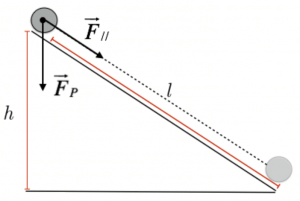
discesa-piano-inclinato — Forza peso che agisce su una biglia in discesa su un piano inclinato.

Sappiamo che il valore della forza peso (componete parallela) che agisce sulla biglia è dato da:

$ F_\\ = F_P * frac (h)(l) = m * g * frac (h)(l) $

Il lavoro che compie la forza peso, quindi, è dato dal prodotto della forza per lo spostamento, quindi vale:

$ L = F_\\ * l = m * g * frac (h)(l) * l = m * g * h $

Ora consideriamo una scala di quattro gradini, ciascuno di altezza rispettivamente $h_1$, $h_2$, $h_3$, $h_4$.

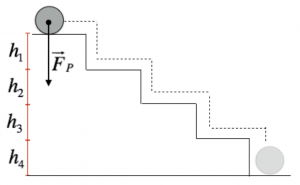
discesa-biglia- energia-potenziale — Discesa di una biglia da una scala composta da gradini.

Quando la biglia scende lungo la scala, la forza peso compie lavoro solo nei tratti verticali; in ciascun tratto il lavoro è dato dal prodotto della forza peso per lo spostamento, e il lavoro totale è dato dalla somma dei singoli lavori:

$ L_Tot = L_1 + L_2 + L_3 + L_4 = F_P * h_1 + F_P * h_2 + F_P * h_3 + F_P * h_4 $

Mettendo in evidenza $F_p$, ci riconduciamo alla formula precedente:

$ L = F_P * (h_1 + h_2 + h_3 + h_4) = F_P * h $

Concludiamo che il lavoro compiuto dalla forza peso nei due esempi precedenti è esattamente lo stesso.

Esempio di forza dissipativa

Un esempio di forza dissipativa è la forza di attrito radente.

Mentre, infatti, nel caso delle forze conservative il lavoro svolto può essere recuperato (per questo il termine “conservative”), per le forze dissipative il lavoro svolto per vincere una determinata forza non può essere più recuperato.

Consideriamo, ad esempio, una scatola che viene fatta salire su di un piano inclinato in presenza di attrito. Per permettere alla scatola di salire è necessario applicare ad essa una forza maggiore della componente parallela della forza peso, così da vincere anche la forza di attrito.

Il lavoro è quindi maggiore di $F_p*h$, dove h è la lunghezza del piano.

Se la scatola, che si trova in cima al piano, ricadesse giù lungo di esso, la forza peso compierebbe un lavoro pari esattamente a $F_P*h$ .

Di conseguenza, il lavoro fatto inizialmente non è più recuperabile.

Si dice che, quando la scatola si trova in cima al piano, essa possiede un’energia potenziale, proprio perché ritornando alla posizione iniziale la forza peso può compiere una lavoro.

L’energia potenziale

Il concetto di energia potenziale può esser applicato a tutte le forze conservative.

Si definisce la variazione di energia potenziale $ ∆U = (U_B – U_A)$ come l’opposto del lavoro che viene fatto dalla forza F durante il tragitto dalla posizione A alla posizione B.

$ ∆U = U_B – U_A = -L_A,B $

In particolare, il valore dell’energia potenziale in un particolare punto dipende dalla scelta del livello zero dell’energia potenziale.

Quindi, una volta scelta una condizione R tale che $U_R = 0$, si definisce energia potenziale in un punto A proprio il lavoro che la forza F compie nel passaggio da A alla situazione di riferimento:

$ ∆U = U_A – U_R = U_A – 0 = U_A = -L_R,A = +L_A,R $

Il concetto di energia potenziale può essere applicato solo al caso di forze conservative; infatti, se avessimo una forza dissipativa, non potremmo parlare di una grandezza pari al lavoro svolto dalla forza F nel passaggio da un punto ad un altro.

Il lavoro, infatti, dipende proprio dal percorso effettuato, e non solamente dal punto iniziale e quello finale. Di conseguenza, tale grandezza sarebbe differente ogni volta che si sceglie un percorso diverso, e non avrebbe senso dare una definizione generale.