Forze che agiscono su un corpo rigido

Forze e corpi rigidi

Come sappiamo, applicando più forze ad un punto materiale, possiamo facilmente determinare la risultante di esse; otteniamo quindi la forza totale mediante la somma vettoriale delle forze.

Nel caso di un corpo rigido, però, abbiamo un’estensione molto grande del corpo rispetto alla superficie di un solo punto; l’effetto di una o più forze applicate al corpo dipende anche dal punto di applicazione delle stesse.

Forze applicate in punti diversi, quindi, provocano effetti diversi.

Ad esempio, consideriamo una bottiglia posta orizzontalmente sul pavimento; supponiamo di applicare una forza al centro della bottiglia: la forza provocherà uno spostamento della bottiglia lungo il piano; se, invece, applichiamo una forza sul collo della bottiglia, provocheremo una rotazione di essa.

Effetti di una forza che agisce in punti diversi su un corpo rigido

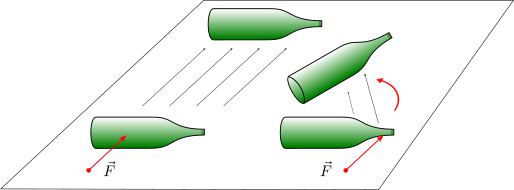
Inoltre, notiamo che l’effetto di una forza che agisce su un corpo rigido non cambia se il suo punto di applicazione viene spostato lungo la retta su cui giace il vettore forza, detta retta d’azione.

Se, invece, applichiamo più forze ad un corpo rigido, per calcolare la risultante dobbiamo tenere presente i diversi punti di applicazione delle forze, e quindi agire in base alle situazioni che si presentano.

Esaminiamo diversi possibili casi che si possono verificare quando applichiamo due forze ad un corpo rigido.

Forze collineari

Le forze collineari sono forze che agiscono sulla stessa retta d’azione su un corpo rigido. In questo caso, possiamo calcolare la risultante delle forze in questo modo: spostiamo una delle due forze ($F_2$) lungo la retta d’azione fino a quando il suo punto di applicazione coincide con quello dell’altra ($F_1$); ora, possiamo calcolare la risultante con la somma vettoriale.

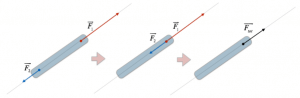
La risultante potrà essere spostata lungo la retta d’azione senza che il suo effetto sul corpo venga modificato. Inoltre, tale risultante può essere nulla nel caso in cui le forze abbiamo verso opposto e stessa intensità.

Forze concorrenti

Le forze concorrenti sono forze le cui rette d’azione si intersecano in un punto. In questo caso, quindi, per calcolare la forza risultante dobbiamo spostare le due forze lungo la retta d’azione fin quando i loro punti di applicazione non sono gli stessi; successivamente, si calcola la forza risultante con la regola del parallelogramma.

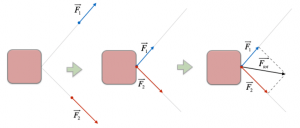
Notiamo che, a differenza delle forze collineari, nel caso delle forze concorrenti la risultante è sempre diversa da zero.

Forze parallele

Le forze parallele sono, come dice il nome, forze che hanno rette d’azione parallele; in particolare, le forze parallele possono essere di due tipi:

si hanno forze parallele concordi quando le forze hanno lo stesso verso (nel caso, ad esempio, di due persone che spostano un armadio spingendo nella stessa direzione);

si hanno forze parallele discordi quando le forze hanno verso opposto (nel caso, ad esempio, di un terremoto, per cui la crosta terrestre scorre sui lati di una faglia);

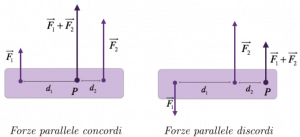
forze-parallele — Forza risultante nel caso di coppie di forze parallele concordi e discordi.

In generale, la forza risultante è applicata in un certo punto P, che si individua grazie alla seguente proporzione:

$ d_1 : d_2 = F_1 : F_2 $

dove, $d_1$ e $d_2$ indicano, rispettivamente, le distanze del punto P dai punti di applicazione di $F_1$ e $F_2$.

In particolare, se le forze sono concordi, il punto P si troverà compreso tra $F_1$ e $F_2$, e il modulo della forza risultante è dato dalla somma dei moduli delle forze che agiscono:

$ F_Tot = F_1 + F_2 $

Inoltre, la posizione del punto P dipende dall’intensità delle forze stesse; se le forze hanno uguale intensità, il punto P sarà equidistante dalle forze, altrimenti sarà più vicino alla forza di intensità maggiore.

Se, invece, le forze sono discordi, il punto P si trova esternamente alle forze; in particolare, esso sarà situato dalla parte della forza di intensità maggiore. Il modulo della forza risultante si ottiene con la differenza dei moduli delle forze che agiscono.

$ F_Tot = F_2 + F_1 $