Energia potenziale gravitazionale e energia potenziale elastica

L’energia potenziale gravitazionale

Quando un corpo si trova ad una certa altezza, come per esempio una scatola sopra ad un tavolo o a una mensola, esso possiede un’energia. Infatti, quando l’oggetto viene lasciato cadere, esso acquista velocità, e quindi possiede energia cinetica, dovuta all’azione della forza di gravità, che compie un lavoro su di esso.

Questa energia si può osservare solo quando il corpo viene messo in movimento, per questo prende il nome di energia potenziale gravitazionale.

Se lasciamo cadere una scatola posta su un tavolo, e una scatola, di uguali dimensioni, posta su una mensola (ad altezza maggiore), notiamo che la scatola posta sulla mensola impiegherà più tempo a cadere, acquistando anche una velocità, e quindi un’energia cinetica, maggiore. Nel primo caso, infatti, la forza peso compie un lavoro maggiore rispetto al secondo caso per far cadere la scatola. Per questo, essa possederà un’energia potenziale gravitazionale maggiore della scatola posta sul tavolo.

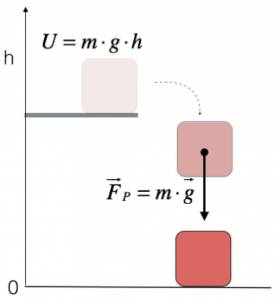
Si definisce l’energia potenziale gravitazionale (U) di un oggetto di massa m posto ad altezza h rispetto al livello zero del sistema di riferimento, il prodotto dell’altezza per la massa per l’accelerazione di gravità:

$ U = m * g * h $

Notiamo che il livello zero del sistema di riferimento è arbitrario, quindi può essere scelto a piacere; l’energia potenziale dell’oggetto dipenderà da tale scelta.

Si può definire l’energia potenziale gravitazionale anche come il lavoro compiuto dalla forza-peso quando il corpo si sposta dalla posizione iniziale (altezza h) a quella di riferimento (livello zero).

ESEMPIO:

Uno scalatore che pesa 750 N porta in spalle l’attrezzatura necessaria e raggiunge l’altezza di 3 m sul livello del mare. Sapendo che il lavoro compiuto dallo scalatore durante la salita è di 2400 J, calcolare la massa dell’attrezzatura.

Dalla definizione di energia potenziale gravitazionale, sappiamo che essa è uguale al lavoro che compie la forza-peso quando il corpo si sposta dalla posizione iniziale a quella di riferimento. Di conseguenza, dai dati forniti dal problema, possiamo affermare che lo scalatore che si trova all’altezza di 3 m sul livello del mare possiede un’energia potenziale gravitazionale di 2400 J.

Dalla formula dell’energia potenziale gravitazionale sappiamo che $ U = M⋅g⋅h $ , dove h = 3 m, g è l’accelerazione di gravità, e M indica la massa complessiva del corpo, quindi la massa dello scalatore più quella dell’attrezzatura.

Dal peso dello scalatore, di 750 N, possiamo ricavare il valore della sua massa, infatti si ha:

$F_P = m_s * g to m_s = frac (F_P)(g) $

Sostituendo i valori numerici abbiamo:

$m_s = frac (F_P)(g) = frac (750 N )(9,8 m/s^2) = 76,53 kg $

Possiamo ricavare la massa dell’attrezzatura da quella dell’energia potenziale gravitazionale:

$ U = m * g * h to M = m_s + m_a = frac (U)(g * h ) to m_a = frac (U)(g * h ) – m_s $

Il valore della massa dell’attrezzatura è quindi:

$ m_a = frac(U)(g * h ) – m_s = frac(2400 J)(9,8 m/s^2 * 3 m ) – 76,53 kg = 5,1 kg $

L’energia potenziale elastica

Come sappiamo, quando una molla viene deformata, quindi viene compressa, o allungata, la forza elastica agisce in verso opposto a quello dello spostamento; la forza, quindi, agisce in modo da far tornare la molla alla posizione di riposo. Di conseguenza, la molla deformata può compiere un lavoro quando viene lasciata andare.

Per questo si dice che essa possiede un’energia potenziale, detta appunto energia potenziale elastica.

In questo caso, il livello zero dell’energia potenziale si ha nella posizione di riposo della molla.

Anche in questo caso possiamo dare una definizione dell’energia potenziale strettamente collegata con il lavoro; infatti, possiamo definire l’energia potenziale elastica come il lavoro che compie la forza elastica quando la molla deformata viene riportata nella sua posizione di riposo.

Notiamo che, in questo caso, il valore dell’energia potenziale elastica sarà sempre positivo; i vettori forza e spostamento, infatti, hanno sempre lo stesso verso, quindi il lavoro compiuto è positivo.

L’energia potenziale elastica può essere calcolata mediante la seguente formula:

$ U_(el) = 1/2 * k * s^2 $

dove k indica la costante elastica della molla, e s lo spostamento della molla, quando viene deformata, rispetto alla posizione di riposo.