Energia meccanica - Matematicamente

L’ Energia meccanica

L’energia cinetica e l’energia potenziale sono due grandezze strettamente collegate, tanto che l’una può “trasformarsi” nell’altra in determinate condizioni.

Ad esempio, consideriamo un oggetto posto ad una certa altezza h rispetto il livello zero dell’energia potenziale. L’oggetto, inizialmente fermo, possiede solo energia potenziale, dovuta all’altezza cui si trova e alla sua massa.

Quando, però, l’oggetto viene fatto cadere, man mano che esso scende la sua altezza rispetto al livello zero diminuisce, e quindi diminuisce anche la sua energia potenziale. Ma, nel frattempo, l’oggetto acquista velocità, dovuta all’azione della forza-peso; di conseguenza, l’oggetto possederà un’energia cinetica sempre maggiore. In prossimità del livello zero, l’energia potenziale sarà praticamente nulla, mentre sarà massima l’energia cinetica.

Trasformazione energia potenziale in energia cinetica durante la caduta del corpo — L’energia potenziale si trasforma in energia cinetica durante la caduta del corpo, cosicché la sua energia totale rimane costante

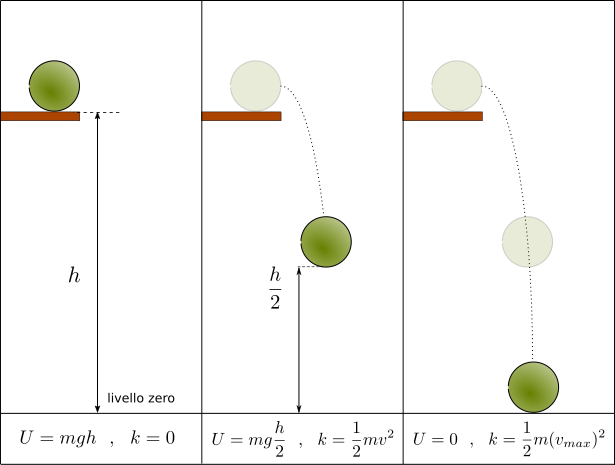
Durante la caduta del corpo, quindi, su ha una diminuzione costante dell’energia potenziale, e un aumento costante dell’energia cinetica, e i due fenomeni avvengono contemporaneamente, come se le energie si trasformassero l’una nell’altra.

In particolare, se non sono presenti attriti nel sistema, possiamo affermare che la somma dell’energia cinetica e dell’energia potenziale (che prende il nome di energia meccanica) rimane sempre uguale; l’energia meccanica, cioè, si conserva.

$ k + U = E_m $

La conservazione dell’energia meccanica, però, avviene solo in determinate condizioni: il sistema fisico che si sta considerando deve essere isolato, cioè non vi devono essere delle forze esterne che agiscono su di esso; inoltre, tutte le forze che agiscono in tale sistema devono essere conservative.

Esempio

Consideriamo un oggetto di massa 8 kg appeso ad un’altezza h = 10 m rispetto al suolo. Se il filo viene tagliato, l’oggetto comincia a cadere sotto l’azione della forza di gravità, e in assenza di forze esterne. Quanto vale la velocità del corpo quando si trova a 4,0 m dal suolo? A quale altezza si trova quando la sua velocità è di 6,0 m/s?

Quando il corpo si trova nella posizione iniziale, esso è fermo, perché appeso al filo. Quindi, l’energia meccanica del corpo è data unicamente dal valore della sua energia potenziale, in quanto l’energia cinetica è nulla:

$ E_m = U + k = U = m*g*h $

Sostituendo i valori numerici abbiamo:

$ E_m = m*g*h = 8,0 kg * 9,8 m/s^2 * 10 m = 784 J $

Quando il corpo si trova a 4 m dal suolo, esso possiede dia energia potenziale che energia cinetica; poiché l’energia meccanica si conserva, la somma di tali energie sarà proprio uguale ad essa.

$ E_m = U + k = m*g*h + 1/2 * m * v^2 $

Da questa formula possiamo ricavare il valore della velocità:

$ E_m – m*g*h = 1/2 * m * v^2 to v^2 = 2*frac(E_m)(m) – 2*g*h to v = sqrt(2*frac(E_m)(m) – 2*g*h) $

Sostituiamo i valori numerici:

$ v = sqrt(2*frac(E_m)(m) – 2*g*h) = sqrt(2*frac(784 J)(8,0 kg) – 2*9,8 m/s^2*4 m) = 10,84 m/s $

Per rispondere al secondo quesito, ricaviamo dalla formula precedente il valore dell’altezza:

$ m*g*h = E_m – 1/2 * m * v^2 to h = frac(E_m)(m*g) – 1/2 * frac (v^2)(g) $

Sostituendo i valori numerici si ottiene:

$ h = frac(784 J)(80 kg * 9,8 m/s^2) – 1/2 * frac ((6 m/2)^2)(9,8 m/s^2) = 10 m – 1,84 m = 8,16 m $

L’energia totale

Molto spesso le situazioni reali sono assai diverse da quelle ideali, e quasi sempre accade che l’energia meccanica di un sistema non si conservi.

Nell’esempio precedente abbiamo visto che quando l’oggetto in caduta si trova in prossimità del livello zero di energia potenziale, quest’ultima è praticamente nulla, mentre l’energia cinetica è massima. Ma cosa accade nel preciso momento in cui l’oggetto raggiunge il suolo, cioè il livello zero?

In questo caso, l’energia potenziale è nulla, ma lo è anche l’energia cinetica, perché l’oggetto cadendo a terra si ferma.

Ciò accade anche, ad esempio, nel caso di un’automobile in frenata: l’energia cinetica che possiede l’automobile viene persa durante la frenata, fino ad esaurirsi completamente quando l’auto è ferma.

Sembra, quindi, apparentemente, che vi sia una perdita di energia.

Consideriamo il caso di oggetti che si muovono con elevata velocità, come ad esempio un proiettile, o un’automobile.

Se riuscissimo a bloccare con le dita un proiettile sparato, ci accorgeremo che esso è caldo; allo stesso modo, quando un’automobile in corsa frena, i dischi dei freni si riscaldano a causa dell’attrito.

Notiamo, quindi, che l’energia che precedentemente sembrava essere sprecata, si è in realtà trasformata in energia interna dei corpi, che viene percepita sotto forma di calore, cioè come aumento della temperature dei corpi stessi.

L’energia interna dei corpi non fa parte dell’energia meccanica; tuttavia, se consideriamo tutte le forme di energia che possono coinvolgere un determinato sistema (ad esempio, l’energia meccanica, interna, elettrica, ecc….), possiamo affermare che in tale sistema (che deve essere isolato) l’energia totale si conserva.