Effetto delle forze sui corpi rigidi, e secondo principio della dinamica

Le forze e l’accelerazione

Come già sappiamo, per il primo principio della dinamica, se un corpo è fermo o si muove a velocità costante, la risultante delle forze che agiscono su di esso è nulla, e il corpo tende a mantenere il suo stato di moto.

Se però, in un sistema di riferimento inerziale, viene applicata una forza ad un corpo, tale forza può modificare il suo stato, provocando in esso un’accelerazione. In particolare, se applichiamo ad un corpo una forza costante, l’accelerazione cui è sottoposto il corpo è anch’essa costante. Il moto del corpo sarà, quindi, un moto uniformemente accelerato.

Questo fatto è stato osservato sperimentalmente utilizzando un disco a ghiaccio secco trainato da un filo.

disco-ghiaccio-secco — Esperimento del disco a ghiaccio secco trainato da un filo.

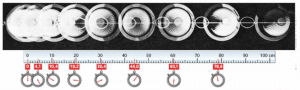
Supponiamo che il disco venga trainato applicando una forza costante, cioè mantenendo sempre uguale l’allungamento dell’elastico; notiamo che in tempi uguali il disco percorre spazi diversi (sempre maggiori mano a mano che procede in avanti); di conseguenza, esso si muove con una velocità variabile, e subisce dunque un’accelerazione. Si può vedere che la distanza percorsa dal disco è direttamente proporzionale al quadrato del tempo impiegato.

Si nota, anche sperimentalmente, che applicando una forza maggiore ad un corpo si ottiene un’accelerazione maggiore; ciò significa che l’accelerazione di un corpo è direttamente proporzionale alla forza che agisce su di esso.

Anche la massa di un corpo influisce sull’accelerazione che il corpo può subire. In particolare, a parità di forza applicata, il corpo più leggero subirà un’accelerazione maggiore del corpo più pesante.

Il secondo principio della dinamica

Le considerazioni fatte precedentemente sono riassunte nel secondo principio della dinamica.

La risultante delle forze applicate ad un corpo è uguale al prodotto della massa (inerziale) del corpo per la sua accelerazione.

$ vec F = m * vec a$

Le forze sono vettori, per questo si può parlare di forza risultante; come sempre, essa è data dalla somma vettoriale delle forze che agiscono sul corpo.

La m che compare nella formula viene definita “massa inerziale”, ed è una quantità caratteristica di ogni corpo; essa, quindi, è indipendente dalla sua forma, ma data dalla quantità di materia che costituisce il corpo stesso.

L’aggettivo “inerziale” riprende il concetto per cui, a parità di forza applicata a corpi di massa diversi, quello di massa maggiore subisce un’accelerazione minore. Possiamo, quindi, dire che questa grandezza esprime come il corpo tenda a conservare la propria velocità, e quindi di come abbia inerzia.

Proprio per questo, la massa viene anche definita come la misura della resistenza che un corpo esercita al tentativo di accelerarlo.

Il secondo principio della dinamica permette anche di dare una definizione alternativa all’unità di misura della forza, il Newton.

Possiamo, infatti, definite 1 N come il valore della forza che si applica ad una massa di $1 kg$ per imprimerle un’accelerazione di $1 m/s^2$.

La caduta libera

Nel caso in cui un oggetto venga lanciato da una certa altezza h, esso tenderà a cadere a terra, in quanto sulla Terra è presente un’accelerazione di gravità ($g = 9,8 m/s^2$) che attrae tutti i corpi che si trovano su di essa.

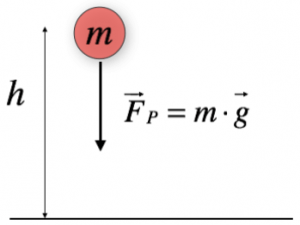
In questo caso, la forza che si ottiene viene definita forza-peso del corpo, o anche peso del corpo.

Esempio:

Consideriamo una massa $m_1$ di 60 kg, e una massa $m_2$ di 75 kg. Si vogliono appendere le due masse ad una fune, collegata ad una carrucola, per trasportarle fino al terzo piano di un edificio. Sapendo che la fune può sostenere, senza rompersi, una forza massima di 1500 N, riuscirà a reggere le due masse?

Per rispondere al quesito dobbiamo calcolare quale forza eserciteranno sulla fune le due masse, appese insieme.

Possiamo, quindi, considerare la massa totale che viene appesa alla fune, data dalla somma delle due:

$ m_Tot = m_1 + m_2 = 60 kg + 75 kg = 135 kg $

Calcoliamo, ora, con il secondo principio, la forza che tale massa esercita sulla fune, considerando come accelerazione quella di gravità:

$ F_Tot = m_Tot * g = 135 kg * 9,8 frac (m)(s^2) = 1323 N $

La forza risultante è minore di quella sopportata dalla fune, che quindi potrà reggere il carico.