Corpi in equilibrio - Matematicamente

Il concetto di equilibrio

Il concetto di equilibrio può essere facilmente compreso, in quanto si presenta in molti aspetti della vita quotidiana. Tutti gli oggetti che ci circondano, e che sono fermi a terra (un tavolo, un mobile, un’auto parcheggiata…) sono in equilibrio.

Possiamo definire, quindi, il concetto di equilibrio affermando che un corpo è in equilibrio quando è fermo e continua a restare fermo.

Il punto materiale

Per studiare l’equilibrio dei corpi, cominciamo dal caso più semplice; consideriamo un corpo piccolissimo rispetto all’ambiente circostante, tale da poter essere considerato come un punto. Per questo, ci riferiremo all’oggetto parlando di punto materiale.

Ad esempio, può essere considerata punto materiale una biglia che rotola sul pavimento.

Il corpo rigido

Nel caso degli oggetti quotidiani, però, non sempre è conveniente utilizzare il concetto di punto materiale. Si considera l’oggetto, quindi, come fosse un corpo rigido, cioè che non subisce deformazioni qualunque siano le forze applicate su di esso.

Anche il corpo rigido è un modello, in quanto non esistono corpi completamente indeformabili; tuttavia, molti oggetti sono indeformabili se vi si applicano forze poco intense.

Le forze vincolari

L’equilibrio dei corpi è influenzato in maniera particolare dai vincoli, cioè da oggetti che impediscono all’oggetto in esame di compiere determinati movimenti nello spazio. Per esempio, un quadro appeso al muro è vincolato dal chiodo nella parete, perché senza di esso cadrebbe a terra; il treno che viaggia sui binari è vincolato da essi, perché costretto a seguire quella traiettoria.

Questi vincoli possono esercitare delle forze sui corpi; in tal caso le forze prendono il nome di reazioni (o forze) vincolari. Una reazione vincolare è quella che si oppone alla nostra forza peso, permettendoci di rimanere in equilibrio e non cadere verso il basso. Il pavimento, quindi, agisce da vincolo, e la reazione vincolare ha stessa intensità della forza peso, stessa direzione, ma verso opposto.

Forza-peso e reazione vincolare del suolo su una persona ferma

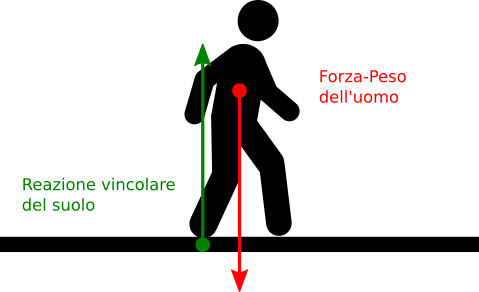
Le forze che si esercitano sul corpo hanno stessa intensità, stessa direzione, ma verso opposto; per le proprietà della somma vettoriale, la risultante delle forze è nulla, e di conseguenza il corpo rimane in equilibrio.

In generale, quindi, un punto materiale rimane in equilibrio se la risultante delle forze che agiscono su di esso è nulla; altrimenti, se la risultante è diversa da zero, il punto non è in equilibrio.

Il piano inclinato

Un oggetto può essere in equilibrio anche se si trova su un piano inclinato; la forza peso che agisce sul corpo si esercita sia spingendo il corpo lungo il piano, sia tenendolo premuto alla superficie.

Per questo, è conveniente scomporre la forza peso nelle sue componenti, che chiamiamo componente parallela ($F_(//)$) e componente perpendicolare ($F_⊥$).

La forza vincolare ($F_v$) ha direzione perpendicolare al piano inclinato, e verso rivolto all’esterno di esso; la componente perpendicolare, che è appunto perpendicolare al piano, ha stessa intensità della forza vincolare, stessa direzione e verso opposto.

La componente parallela, invece, è parallela al piano, e rivolta verso il basso; per tenere in equilibrio un punto materiale sul piano inclinato, quindi, è necessaria la presenza di una forza che annulli la componente parallela; essa deve essere parallela al piano, e deve avere stessa intensità e verso opposto a quello della componente parallela.

La forza prende il nome di forza equilibrante; essa è esercitata dall’esterno del sistema, ed è necessaria per tenere in equilibrio l’oggetto; può essere, ad esempio, la forza di una persona che regge un carrello lungo una salita.

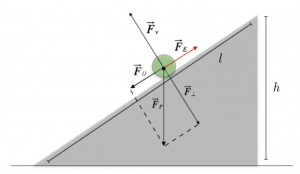
equilibrio-piano-inclinato — Forze agenti su un punto materiale in equilibrio su un piano inclinato.

Il modulo della forza equilibrante può essere ottenuto dalla seguente formula:

$F_e = F_p * frac(h)(l) $

dove, $F_p$ è la forza peso dell’oggetto, h è l’altezza del punto più alto del piano inclinato, e l è la sua lunghezza (se il piano ha forma triangolare, l è l’ipotenusa).

Notiamo, quindi, che più è inclinato il piano, cioè maggiore è il rapporto h/l, tanto più grande deve essere la forza da esercitare per mantenere in equilibrio il nostro oggetto.