Risoluzione di un circuito - Matematicamente

Molto spesso, negli esercizi di fisica, si richiede di risolvere un circuito, cioè determinare il valore delle tensioni ai capi di tutti resistori, e intensità e verso di tutte le correnti presenti nel circuito.

Vediamo un esempio di risoluzione di un circuito:

Esercizio

Consideriamo un circuito come quello in figura:

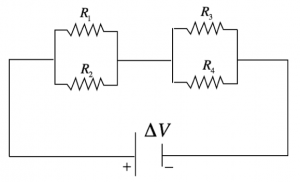
risoluzione-di-un-circuito

Sappiamo che il generatore mantiene una differenza di potenziale ∆V = 28,0 V, e le resistenze presenti valgono rispettivamente:

$ R_1 = 300 Ω , R_2 = 200 Ω $

$ R_3 = 240 Ω , R_4 = 480 Ω $

Per risolvere il circuito e determinare le correnti e le differenze di potenziale che attraversano ogni resistore, dobbiamo trasformare il circuito in un circuito più semplice, in cui sia presente una sola resistenza, la resistenza equivalente.

Per prima cosa, notiamo che sono presenti del circuito quattro resistenze, disposte in due blocchi collegati in serie, e in ogni blocco le resistenze sono collegate in parallelo.

Cominciamo, quindi, eliminando i blocchi, e cosicché nel circuito figurino solo resistenze in serie. La resistenza equivalente per i collegamenti in parallelo si ottiene dal suo reciproco; per il primo blocco, quindi, abbiamo:

$ frac(1)(R_(1,2)) = frac(1)(R_(1)) + frac(1)(R_(2)) = frac(1)(300 Ω) + frac(1)(200Ω) = frac(5)(600 Ω) $

$ R_(1,2) = 120 Ω $

mentre per il secondo:

$ frac(1)(R_(3,4)) = frac(1)(R_3) + frac(1)(R_4) = frac(1)(240 Ω) + frac(1)(480Ω) = frac(3)(480 Ω) $

$ R_(3,4) = 160 Ω $

Il circuito che ora dobbiamo risolvere si presenta in questa forma:

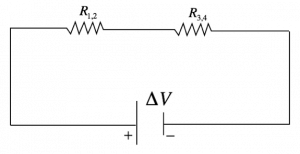
risoluzione-di-un-circuito

Procediamo, ora, calcolando la resistenza equivalente del sistema, che in questo caso è data dall’unione di due resistenze in serie:

$R_(eq) = R_(1,2) + R_(3,4) = 120 Ω + 160 Ω = 280 Ω $

Il circuito equivalente che abbiamo creato si presenta ora in questa forma, con una sola resistenza:

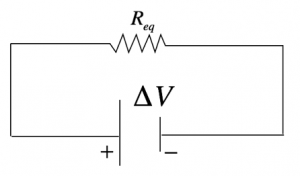
risoluzione-di-un-circuito

Conoscendo la differenza di potenziale creata dal generatore, siamo in grado di calcolare l’intensità di corrente che attraversa in circuito:

$ i_(eq) = frac(∆V)(R_(eq)) = frac(28,0V)(280Ω) = 0,1 A$

Procedendo a ritroso, possiamo ora ottenere tutte le informazioni relative a ciascun resistore.

L’intensità di corrente che abbiamo determinato è la stessa sia per $R_(1,2)$ che per $R_(3,4)$, perché esse sono collegate in serie; calcoliamo, quindi, la differenza di potenziale ai loro capi:

$∆V_(1,2) = i_(eq) * R_(1,2) = 0,1 A * 120Ω = 12V $

$∆V_(3,4) = i_(eq) * R_(3,4) = 0,1 A * 160Ω = 16V $

Poiché le resistenze 1, 2, 3, 4 sono collegate in parallelo a due a due, sono sottoposte alla stessa differenza di potenziale ai loro capi; di conseguenza abbiamo che:

$ ∆V_1 = ∆V_2 = 12V $

$ ∆V_3 = ∆V_4 = 16V $

Procediamo, ora, determinando l’intensità di corrente da cui sono attraversate:

$ i_1 = frac(∆V_1)(R_1) = frac(12V)(300Ω) = 0,04 A , i_2 = frac(∆V_2)(R_2) = frac(12V)(200Ω) = 0,06 A $

$ i_3 = frac(∆V_3)(R_3) = frac(16V)(240Ω) = 0,067 A , i_4 = frac(∆V_4)(R_4) = frac(16V)(480Ω) = 0,033 A $

Abbiamo, quindi, risolto il circuito.

In alcuni casi, però, può capitare che all’interno di un circuito siano presenti due o più generatori; in questo caso, la risoluzione del circuito avviene in maniera differente, in quanto la forma del circuito e la disposizione dei resistori può essere a volte complicata.

In questo caso, un valido aiuto nella risoluzione dei circuiti viene dalle leggi di Kirchhoff, che possono essere applicate per qualunque circuito ohmico, cioè nel quale siano presenti conduttori ohmici e generatori di tensione.

La legge dei nodi

La prima legge di Kirchhoff si definisce anche legge dei nodi, dove per nodo si intende il punto in cui convergono e si uniscono tre o più conduttori. Tale legge afferma che la somma delle correnti entranti un un nodo è uguale alla somma delle correnti uscenti da esso.

La prima legge di Kirchhoff si può anche formulare dicendo che la somma algebrica delle correnti che attraversano un nodo è sempre uguale a zero; in questo caso, si assume che le correnti entranti nel nodo abbiano segno positivo, mentre quelle uscenti segno negativo. Sulla base di questa affermazione, possiamo evidenziare il fatto che vi è conservazione della carica elettrica.

La legge delle maglie

La seconda legge di Kirchhoff è anche detta legge delle maglie, dove per maglie si intendono tratti chiusi di circuito; questa legge afferma che la somma algebrica delle differenze di potenziale che si incontrano percorrendo una maglia è uguale a zero.

Ciò significa che, percorrendo una maglia e partendo da una certa differenza di potenziale, alla fine del percorso si ritorna allo stesso potenziale di partenza.