Moto di una carica in un campo magnetico

Una carica puntiforme che si muove con velocità v all’interno di un campo magnetico è sottoposta alla forza di Lorentz; tale forza, agendo sulla carica, ne modifica la traiettoria, costringendola a seguire un moto ben preciso.

Come abbiamo visto precedentemente, la forza di Lorentz che agisce sulla carica ha direzione perpendicolare a quella della sua velocità, e quindi anche a quella dello spostamento.

Come sappiamo, nel caso in cui forza e spostamento siano perpendicolari, il lavoro compiuto dalla forza (dato dal prodotto scalare di forza e spostamento) è nullo.

Dal teorema dell’energia cinetica, sappiamo che la differenza di energia cinetica di un corpo è uguale al lavoro che viene svolto dalla forza che agisce su di esso; in questo caso, quindi, anche l’energia cinetica è nulla.

Il fatto che un corpo non subisca variazione di energia cinetica significa che la sua velocità rimane costante in modulo.

Possiamo quindi affermare che la forza di Lorentz che agisce su una particella non modifica il modulo della sua velocità, ma soltanto la sua traiettoria: ciò che cambia, quindi, è la direzione e il verso della velocità della particella.

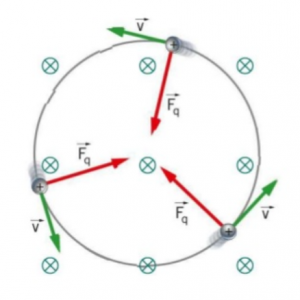
Un moto uniforme che riflette queste stesse caratteristiche è quello circolare, in cui la forza è centripeta, rivolta cioè verso il centro della circonferenza, e perpendicolare i ogni punto alla velocità tangenziale.

In effetti, si può dimostrare che il moto che viene descritto da una particella all’interno di un campo magnetico è proprio un moto circolare uniforme.

In questo caso, se il campo magnetico è uniforme, la forza di Lorentz è costante, e vale F = qvB (perché i vettori sono perpendicolari, e quindi si ha sen 90° = 1), ed è sempre perpendicolare sia alla velocità della particelle, sia al campo magnetico.

Conoscendo l’espressione della forza di Lorentz, e quella della forza centripeta, e sapendo che in questo caso le due forze coincidono, possiamo determinare ulteriori informazioni sul moto che compie la particella; ad esempio, possiamo ricavare il raggio della circonferenza che essa descrive.

$F_q = q*v*B , F_c = m * frac(v^2)(r) to r = frac(m * v)(q * B) $

dove m indica la massa della particella, v la sua velocità, q la sua carica, e B il campo magnetico cui essa è sottoposta.

La velocità della particella, in un moto circolare uniforme, si esprime come rapporto tra la lunghezza della circonferenza e il periodo di rotazione:

$ v = frac(2πr)(T)$

Sostituendo questa formula nell’espressione precedente, possiamo esprimere anche il periodo del moto circolare in funzione delle altre grandezze:

$ r = frac(m * v)(Q * B) = frac(m)(q * B) * frac(2πr)(T) to T = frac(2πm)(q*B)$

Il moto elicoidale

Una particella che si muove in un campo magnetico non sempre ha velocità perpendicolare alla direzione del campo magnetico.

Nel caso in cui si formi un angolo particolare tra i due vettori, la traiettoria descritta dalla particella non è quella di un moto circolare uniforme.

In questo caso, si scompone la velocità nelle sue componenti, delle quali una è perpendicolare al campo magnetico, mentre l’altra è parallela ad esso.

Notiamo così, che il moto descritto dalla velocità parallela è rettilineo uniforme, mentre quello descritto dalla componente perpendicolare è circolare uniforme.

Poiché entrambe le velocità sussistono contemporaneamente, il moto totale è dato dalla sovrapposizione dei due moti precedenti, cosicché il moto risultante è descritto da un’elica cilindrica a passo costante, io tale che la distanza tra una “circonferenza” e l’altra è sempre la stessa.

traiettoria-elicoidale — Traiettoria elicoidale della particella.

In questo caso, il raggio dell’elica si può ricavare sempre dalla formula vista precedentemente, sostituendo però al posto della velocità v, la sua componente perpendicolare:

$ r_c = frac(m * v_⊥)(q * B)$