Un condensatore piano è un dispositivo costituito da due piastre metalliche parallele, che prendono il nome di armature; esse sono poste ad una certa distanza l’una dall’altra.
Per far funzionare l’apparecchio, le lastre vengono caricate con cariche di segno opposto.
Vediamo ora come di procede per caricare un condensatore piano.
Ipotizziamo che, inizialmente, entrambe le armature siano messe a terra, e posseggano quindi lo stesso potenziale della terra.
Se poi una di esse viene caricata con una carica Q positiva, e l’altra rimane a terra, automaticamente sulla faccia interna di quest’ultima si induce una carica pari a -Q (l’elettrizzazione della seconda lastra avviene per induzione).
La capacità
Quando conferiamo la carica Q alla prima lastra, essa passa da un potenziale elettrico pari a zero al potenziale V; per via sperimentale si nota che la carica che si trova sul conduttore è direttamente proporzionale al potenziale che essa assume.
E’ utile, quindi, introdurre una nuova grandezza, valida per qualsiasi conduttore isolato che passa da uno stato iniziale a potenziale nullo ad uno stato finale a potenziale V.
Questa nuova grandezza si definisce capacità elettrostatica del conduttore, e si indica come rapporto tra la carica Q e il potenziale elettrico:
$C = Q/V$
La capacità di un conduttore si indica, nel Sistema Internazionale, in farad (F), dal nome del fisico Michael Faraday che si cimentò in questi studi.
Anche nel caso di un condensatore piano, essendo esso un conduttore, possiamo parlare ci capacità; in questo caso, si definisce capacità del condensatore come il rapporto tra la carica assunta dalla prima lastra e la divergenza di potenziale tra le due armature:
$C = frac(Q)(∆V)$
Come nel caso di un conduttore generico, anche la capacità del condensatore dipende dalla sua forma e dalle sue dimensioni.
Il campo elettrico
Il condensatore piano può essere rappresentato, in maniera ideale, considerando due distribuzioni piane infinite di carica, parallele, e poste ad una certa distanza l’una dall’altra.
Come abbiamo visto nel caso della distribuzione piana infinita di carica, è possibile trovare una formula che esprima il campo elettrico generato da tale distribuzione. Il campo elettrico, in quel caso, era dato dal rapporto:
$E = frac(σ)(2ε)$
In un condensatore si ha una situazione leggermente diversa; in ogni punto dello spazio, interno o esterno alle due lastre, il campo elettrico totale è dato dalla somma (vettoriale) del campo elettrico generato da ciascuna delle due piastre.
Ricordiamo che il vettore campo elettrico è entrante per la lastra con carica negativa, e uscente per la piastra con carica positiva.
E’ possibile, quindi, dedurre che all’esterno delle due lastre il contributo al campo elettrico di ciascuna di esse fa si che il campo elettrico totale sia nullo; all’interno di esse, invece, il campo elettrico è doppio rispetto a quello generato da ogni singola armatura.
Inoltre, all’interno delle armature, il campo elettrico è uniforme, e il vettore ha direzione ortogonale alle lastre, e verso diretto da quella positiva a quella negativa.
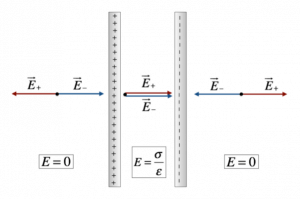
L’intensità del campo elettrico, quindi, si deduce dalla formula di quello di una distribuzione piana infinita di carica, moltiplicando questo per due:
$E = frac(σ)(ε)$
Capacità del condensatore conoscendo il campo elettrico
Conoscendo l’espressione dell’intensità del campo elettrico, possiamo dedurre la capacità del condensatore in un’altra espressione.
Ricordiamo che è possibile esprimere il modulo cel campo elettrico come rapporto tra la differenza di potenziale e ∆s, che in questo caso equivale alla distanza tra le due armature, e che indichiamo con d; svolgiamo, quindi, i passaggi:
$ E = frac(∆V)(∆S) = frac(∆V)(d) to ∆V = E * d = frac(σ)(ε) * d$
La densità superficiale di carica, inoltre, può essere espressa come rapporto tra la carica e la superficie, cioè l’area di un’armatura:
$ σ = Q/S to ∆V = frac(σ)(ε) * d = frac(Q)(S) * frac(d)(ε) $
Poiché la capacità del condensatore è data dal rapporto tra la carica Q e la differenza di potenziale, abbiamo la formula cercata:
$C = frac(Q)(∆V) = frac(Q)(frac(Q)(S) * frac(d)(ε)) = frac(S * ε)(d)$
Potrebbero interessarti
Video Lezioni: Elettromagnetismo
Vide Lezioni: Onde e Luce
Appunti: Il teorema di Coulomb
Appunti: Il campo elettrico
Appunti: Le linee di campo
Appunti: Campi elettrici con particolari simmetrie
Appunti: Condensatori in seire e in parallelo
Appunti: La corrente elettrica e i circuiti
Appunti: La prima legge di Ohm e i resistori
Appunti: Risoluzione di un circuito
Appunti: L’effetto Joule
Appunti: La forza elettromotrice
Appunti: La conduzione elettrica nei metalli
Appunti: Processo di carica e scarica di un condensatore
