Re: Strana sucessione, Quand'è che converge?
08/11/2023, 10:22
Sia x il limite della successione convergente per un certo k > 0.
Allora, al tendere all'infinito dell'indice della successione deve essere x = k^x, ossia:
k = x^1/x).
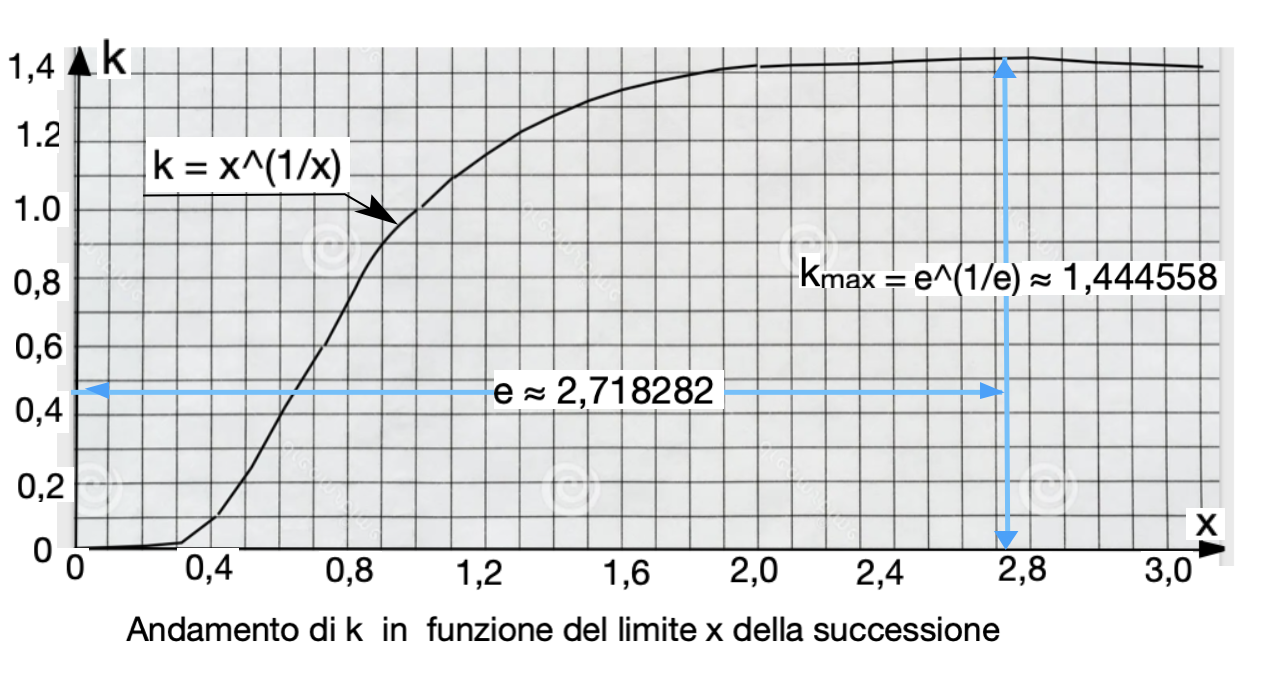
Il massimo do k in funzione di x è_
Kmax = e^(1/e).
Pertanto la risposta al quiz è:
0 < k ≤ e^(1/e).
Allora, al tendere all'infinito dell'indice della successione deve essere x = k^x, ossia:
k = x^1/x).

Il massimo do k in funzione di x è_
Kmax = e^(1/e).
Pertanto la risposta al quiz è:
0 < k ≤ e^(1/e).
Re: Strana sucessione, Quand'è che converge?
12/11/2023, 21:43
Per valori piccoli di $k$ la successione oscilla su due valori.
Mi sembra che lo faccia per $k < 0.066$ circa, determinato graficamente.
Mi sembra che lo faccia per $k < 0.066$ circa, determinato graficamente.
Re: Strana sucessione, Quand'è che converge?
14/11/2023, 12:11
A memoria era una potenza con tante "$e$", mi sembra $e^-e$, e guardando con Wolframalpha sembrerebbe tornare con quello che dice Quinzio, anche se mi ricordo che non ero riuscito a dimostrarla questa cosa.
EDIT: ah ma l'aveva scritto già hydro, eh vabbè, non me n'ero accorto.
EDIT: ah ma l'aveva scritto già hydro, eh vabbè, non me n'ero accorto.
Re: Strana sucessione, Quand'è che converge?
14/11/2023, 12:43
Quindi abbiamo capito che per $k$ abbastanza piccolo la successione arriva ad oscillare tra due valori distinti. Qualcuno sa quali siano questi due valori? (In funzione di $k$ ovviamente).
Re: Strana sucessione, Quand'è che converge?
14/11/2023, 14:52
Martino ha scritto:Quindi abbiamo capito che per $k$ abbastanza piccolo la successione arriva ad oscillare tra due valori distinti. Qualcuno sa quali siano questi due valori? (In funzione di $k$ ovviamente).
Si verifica facilmente che per $k<e^{-e}$ la funzione $k^{k^x}$ ha due punti fissi $x_0,x_1$. Non ho fatto i conti ma immagino che ci sia un $2$-ciclo $x_0\mapsto k^{x_1}\mapsto k^{k^{x_1}}=x_0$ attrattivo.
Re: Strana sucessione, Quand'è che converge?
14/11/2023, 15:28
Sì credo anch'io, ma $x_0$ si può calcolare? (In funzione di $k$).
Re: Strana sucessione, Quand'è che converge?
14/11/2023, 21:23
Martino ha scritto:Sì credo anch'io, ma $x_0$ si può calcolare? (In funzione di $k$).
Mi vien da dire di no.
E' la soluzione di $x = k^{k^x}$ o se si preferisce, di $root{x}x = k^k$
Re: Strana sucessione, Quand'è che converge?
15/11/2023, 13:10
Se non ho frainteso, fissato \(x > 0\) e definita la successione di numeri reali per ricorrenza: \[
a_0 = x,
\quad \quad
a_n = x^{a_{n-1}}
\quad \quad
\text{con} \; n=1,2,3,\dots
\] si richiede il calcolo del limite \(y := \begin{aligned}\lim_{n \to +\infty} a_n\end{aligned}\), ammesso che esista.
Da esperimenti numerici ho potuto constatare che:
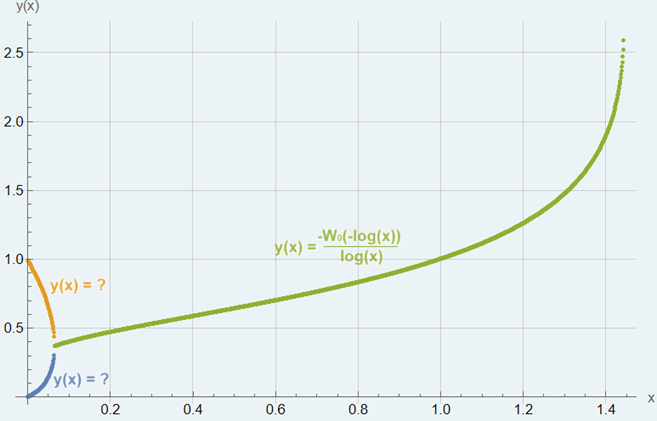
mentre graficando per punti \(x\) in funzione di \(y\) otteniamo:
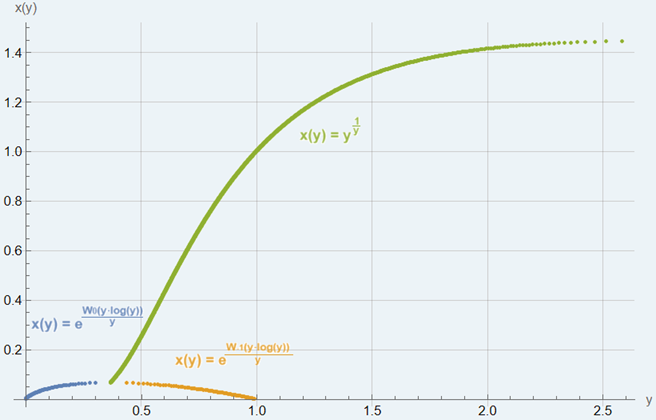
dove è stato fatto uso della funzione W di Lambert.
a_0 = x,
\quad \quad
a_n = x^{a_{n-1}}
\quad \quad
\text{con} \; n=1,2,3,\dots
\] si richiede il calcolo del limite \(y := \begin{aligned}\lim_{n \to +\infty} a_n\end{aligned}\), ammesso che esista.
Da esperimenti numerici ho potuto constatare che:
- se \(x > e^{\frac{1}{e}}\) allora molto semplicemente \(y = +\infty\);
- se \(e^{-e} \le x \le e^{\frac{1}{e}}\) allora \(y = \begin{cases}
\frac{-W_0(-\log(x))}{\log(x)} & \text{se} \; x \ne 1 \\
1 & \text{se} \; x = 1 \\
\end{cases}\), che verifica l'equazione \(y = x^y\); - se \(0 < x < e^{-e}\) allora \(\not\exists\,y\), in quanto per \(n\) pari si ottiene \(y_{\min}\) e per \(n\) dispari si ottiene \(y_{\max}\) stimabili risolvendo numericamente l'equazione \(y = x^{\left(x^y\right)}\). Ad esempio, se \(x = 0.06\) tale equazione è verificata per \(y \approx 0.216898\) o \(y \approx 0.36158\) o \(y \approx 0.54323\), da cui si ha \(y_{\min} \approx 0.216898\) e \(y_{\max} \approx 0.54323\).

mentre graficando per punti \(x\) in funzione di \(y\) otteniamo:

dove è stato fatto uso della funzione W di Lambert.
Skuola.net News è una testata giornalistica iscritta al Registro degli Operatori della Comunicazione.
Registrazione: n° 20792 del 23/12/2010.
©2000—
Skuola Network s.r.l. Tutti i diritti riservati. — P.I. 10404470014.
Powered by phpBB © phpBB Group - Privacy policy - Cookie privacy
phpBB Mobile / SEO by Artodia.