Un limite… radicale
04/05/2024, 07:56
Calcolare
$$\lim_{n \rightarrow +\infty} \frac{1}{n} \sum_{k=1}^{n} n^{1/k}$$
$$\lim_{n \rightarrow +\infty} \frac{1}{n} \sum_{k=1}^{n} n^{1/k}$$
Re: Un limite… radicale
04/05/2024, 09:05
Testo nascosto, fai click qui per vederlo
$$\lim_{n \rightarrow +\infty} \frac{1}{n} \sum_{k=1}^{n} n^{1/k} = 1+ n^{-\frac{1}{2}}+ n^{-\frac{2}{3}}+ n^{-\frac{3}{4}}+ ... = 1$$
Tutti quei termini vanno a 0, ma non sono sicuro al 100%.
Tutti quei termini vanno a 0, ma non sono sicuro al 100%.
Re: Un limite… radicale
04/05/2024, 09:12
@Quinzio
Attento al segno all’ esponente
Attento al segno all’ esponente
Re: Un limite… radicale
05/05/2024, 21:19
Mmm... Non credo che il risultato di Quinzio sia giusto. Posto $S_n=sum_(k=1)^n n^(1/k)$ ed arrotondando i risultati ottengo $S_1=1; S_2=1.71; S_3=2.06; S_4=2.25$ e queti numeri fanno pensare ad una successione crescente, forse con limite $e$. Ma non è certo una dimostrazione!
Re: Un limite… radicale
06/05/2024, 16:15
@Giammaria
Il risultato di quinzio non è corretto.
Il limite è …
Il risultato di quinzio non è corretto.
Il limite è …
Testo nascosto, fai click qui per vederlo
2
Re: Un limite… radicale
07/05/2024, 07:25
Ne sei sicuro? Con la mia notazione ed aiutandomi con un foglio di calcolo, trovo $S_(10)=2.542$, che mi conferma nella mia ipotesi.
Re: Un limite… radicale
07/05/2024, 08:38
Testo nascosto, fai click qui per vederlo
Per \(k \ge 2\) si ha: \[
\begin{aligned}
& 1 \le \left(1\cdot 1\cdots 1\cdot\sqrt{n}\cdot\sqrt{n}\right)^{1/k} \le \frac{1+1+\dots+1+\sqrt{n}+\sqrt{n}}{k} \\
\\
& 1 \le n^{1/k} \le \frac{k-2+2\sqrt{n}}{k} \\
\\
& \sum_{k=2}^n 1 \le \sum_{k=2}^n n^{1/k} \le \sum_{k=2}^n \frac{k-2+2\sqrt{n}}{k} \\
\\
& n-1 \le \sum_{k=1}^n n^{1/k}-n \le \sum_{k=1}^n \frac{k-2+2\sqrt{n}}{k}+1-2\sqrt{n} \\
\\
& 2n-1 \le \sum_{k=1}^n n^{1/k} \le n-2H_n+2\sqrt{n}\,H_n+1-2\sqrt{n}+n \\
\\
& \frac{2n-1}{n} \le \frac{1}{n}\sum_{k=1}^n n^{1/k} \le \frac{2n-2(1-H_n)\sqrt{n}+1-2H_n}{n} \\
\end{aligned}
\] Siccome: \[
\lim_{n\to\infty}\frac{2n-1}{n}=\lim_{n\to\infty}\frac{2n-2(1-H_n)\sqrt{n}+1-2H_n}{n}=2
\] per il teorema del confronto: \[
\boxed{\lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^n n^{1/k}=2\,}
\]Volendo vedere che succede graficamente, in Mathematica possiamo scrivere:
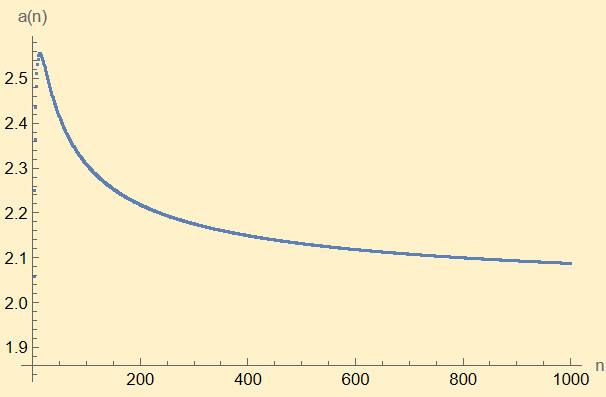
ed effettivamente si può intuire che, seppur raggiungibile lentamente, il limite può essere \(2\).
\begin{aligned}
& 1 \le \left(1\cdot 1\cdots 1\cdot\sqrt{n}\cdot\sqrt{n}\right)^{1/k} \le \frac{1+1+\dots+1+\sqrt{n}+\sqrt{n}}{k} \\
\\
& 1 \le n^{1/k} \le \frac{k-2+2\sqrt{n}}{k} \\
\\
& \sum_{k=2}^n 1 \le \sum_{k=2}^n n^{1/k} \le \sum_{k=2}^n \frac{k-2+2\sqrt{n}}{k} \\
\\
& n-1 \le \sum_{k=1}^n n^{1/k}-n \le \sum_{k=1}^n \frac{k-2+2\sqrt{n}}{k}+1-2\sqrt{n} \\
\\
& 2n-1 \le \sum_{k=1}^n n^{1/k} \le n-2H_n+2\sqrt{n}\,H_n+1-2\sqrt{n}+n \\
\\
& \frac{2n-1}{n} \le \frac{1}{n}\sum_{k=1}^n n^{1/k} \le \frac{2n-2(1-H_n)\sqrt{n}+1-2H_n}{n} \\
\end{aligned}
\] Siccome: \[
\lim_{n\to\infty}\frac{2n-1}{n}=\lim_{n\to\infty}\frac{2n-2(1-H_n)\sqrt{n}+1-2H_n}{n}=2
\] per il teorema del confronto: \[
\boxed{\lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^n n^{1/k}=2\,}
\]Volendo vedere che succede graficamente, in Mathematica possiamo scrivere:
- Codice:
ListPlot@Table[NSum[n^(1/k - 1), {k, n}], {n, 1000}]

ed effettivamente si può intuire che, seppur raggiungibile lentamente, il limite può essere \(2\).
Re: Un limite… radicale
07/05/2024, 09:19
@giammaria
Calcola con valori grandi di $n$
@sellacollesella
Ok
Calcola con valori grandi di $n$
@sellacollesella
Ok
Re: Un limite… radicale
07/05/2024, 14:16
Per capire il primo passaggio della dimostrazione di sellacollesella (che non e' banale):
https://it.wikipedia.org/wiki/Disuguagl ... geometrica
https://it.wikipedia.org/wiki/Disuguagl ... geometrica
Re: Un limite… radicale
08/05/2024, 06:30
Effettivamente trovo $S_40=2,448<S_10$. Beì, è insolito che una successione prima cresca e poi decresca.
Skuola.net News è una testata giornalistica iscritta al Registro degli Operatori della Comunicazione.
Registrazione: n° 20792 del 23/12/2010.
©2000—
Skuola Network s.r.l. Tutti i diritti riservati. — P.I. 10404470014.
Powered by phpBB © phpBB Group - Privacy policy - Cookie privacy
phpBB Mobile / SEO by Artodia.