sto preparando l'esame di programmazione matematica alias ricerca operativa.
non ho capito nulla per quanto riguarda la ricerca di massimi e minimi di una funzione di due variabili soggetta a vincoli o di uguaglianza o disuguaglianza o entrambi. per esempio:
determinare i punti stazionari, i massimi e i minimi assoluti (se ci sono) e i moltiplicatori di:
x^3 + y^2
soggetta ai vincoli:
x^2 - y^2 <= 1; x >= 1/4
come si risolvono questi esercizi?
9 messaggi
• Pagina 1 di 1
Non hai fatto Analisi II, o l'equivalente di ora? E' uno standard esercizio di massimi e minimi vincolati.
Luca77
http://www.llussardi.it
Luca77
http://www.llussardi.it
- Luca77
so come funziona il metodo classico ovvero senza moltiplicatori e senza vincoli. in pratica, si imposta il sistema composto dalle derivate parziali prime uguagliate a zero: è la condizione necessaria.
si troveranno i punti stazionari. poi si determina la matrice hessiana e si trova una funzione. si introducono i punti stazionari di prima nell'hessiano e si trovano dei valori. si considerano solo quelli >0.
sono i potenziali massimi o minimi: per vedere il minimo, ad esempio, si considera la derivata parziale seconda rispetto a x, e si introduce nella funzione così trovata i punti dove l'hessiano era positivo. se trovo un valore negativo, quello è un massimo, altrimenti è un minimo.
come si fa a risolvere un esercizio tipo quello che ho scritto nel primo post?
si troveranno i punti stazionari. poi si determina la matrice hessiana e si trova una funzione. si introducono i punti stazionari di prima nell'hessiano e si trovano dei valori. si considerano solo quelli >0.
sono i potenziali massimi o minimi: per vedere il minimo, ad esempio, si considera la derivata parziale seconda rispetto a x, e si introduce nella funzione così trovata i punti dove l'hessiano era positivo. se trovo un valore negativo, quello è un massimo, altrimenti è un minimo.
come si fa a risolvere un esercizio tipo quello che ho scritto nel primo post?
- mica81
- Junior Member

- Messaggio: 96 di 135
- Iscritto il: 08/04/2003, 10:34
- Località: Italy
La trattazione generale del problema di trovare il massimo [o il minimo] di una funzione non lineare di più variabili soggetta a vincoli anch’essi non lineari è assai complessa e non esiste, almeno che io sappia, un metodo che garantisca la soluzione nella totalità dei casi. Se circoscriviamo il problema alle funzioni di due variabili [x e y] possiamo impostarlo nel seguente modo…
Trovare il massimo [o il minimo] di una funzione f(x,y) definita in un certo campo A sottoposta ad una serie di vincoli del tipo…
g1(x,y)>=0, g2(x,y)>=0,…,gk(x,y)>=0 [1]
L’insieme dei vincoli descriverà quella porzione del piano x,y nella quale si dovrà trovare il punto [xo,yo] che massimizza [o minimizza] la funzione f(x,y). Mentre nel caso lineare [ossia con la f e le g funzioni lineari di x e y] si sà che il punto cercato, se esiste, è un punto estremo [ossia è un punto in cui due dei vincoli si riducono a eguaglianze, in pratica in corrispondenza dell’angolo formato da due segmenti] nel caso non lineare la trattazione è un poco più complessa. Una strategia possibile è la seguente…
a)si trovano tutti i massimi [o minimi]relativi della funzione f(*) non vincolati
b)si determina quali dei massimi [o minimi] trovati in a) sono compatibili con i vincoli
c)si sceglie dei punti trovati in a) e b) quello al quale corrisponde il valore massimo [o minimo] di f(*) e lo si chiama [x*,y*]
d)per ognuno dei k vincoli, applicando il metodo dei moltiplicatori di Lagrange, si trova il valore di x e y che massimizza [o minimizza] f(*) con la condizione gi(x,y)=0 per i=1,2,...,k. Se tale punto di massimo [o minimo] esiste ed è compatibile con gli altri vincoli lo si indica con [xk,yk]
e)supposto k>1, per ognuna delle n=k*)k-1)/2 coppie di vincoli si calcolano i punti estremi, definiti come le soluzione delle coppie di eqiazioni gi(x,y)=0,gj(x,y)=o con i<>j e si consoderano solo quelli compatibili con gli altri vincoli. Tra queli punti così trovati si sceglie quello per cui f(*) ha il valore massimo [o minimo] e lo si indica con [xm,ym] per m=1,2,...,n
f)tra i vettori a due dimensioni [x,y] trovati in c),d) ed e) si sceglie quello al quale corrisponde il valore massimo [o minimo] di f(*). Se tale punto esiste, esso sarà la soluzione del problema…
Nel caso illustrato da mica81 [non particolarmente utile come esempio…] si ha…
f(x,y)= x^3+y^2
g1(x,y)=x-1/4
g2(x,y)=y^2-x^2+1 [2]
Il problema consiste nel trovare il valore che rende massima la funxione f(*)=x^3+y^2 nei punti del piano x,y che hanno ascissa…
¼<=x<=sqr (y^2+1) [3]
… e nessun limite per l’ordinata. La ricerca del massimo assoluto di f(*) senza vincoli rivela che essa non ha massimi né minimi in nessun punto del piano x,y. La ricerca eseguita sulla retta x=1/4 [g1(*)=0] rivela un solo punto di minimo [e non di massimo] per y=0 e in essa si ha f(*)=1/64. La ricerca eseguita sulla curva y=sqr(x^2-1) [g2(*)=0] rivela che vi è un punto di minimo [e non di massimo] in [1,0], e lì la fuznione vale 1. In conclusione la fuiznione non presenta massimi e si ha un minimo in [1/4,0] che vale 1/64. In effetti il problema proposto come esempio non è dei più interessanti. Ritengo però si possa certamente fare una scelta migliore…
cordiali saluti
lupo grigio

Trovare il massimo [o il minimo] di una funzione f(x,y) definita in un certo campo A sottoposta ad una serie di vincoli del tipo…
g1(x,y)>=0, g2(x,y)>=0,…,gk(x,y)>=0 [1]
L’insieme dei vincoli descriverà quella porzione del piano x,y nella quale si dovrà trovare il punto [xo,yo] che massimizza [o minimizza] la funzione f(x,y). Mentre nel caso lineare [ossia con la f e le g funzioni lineari di x e y] si sà che il punto cercato, se esiste, è un punto estremo [ossia è un punto in cui due dei vincoli si riducono a eguaglianze, in pratica in corrispondenza dell’angolo formato da due segmenti] nel caso non lineare la trattazione è un poco più complessa. Una strategia possibile è la seguente…
a)si trovano tutti i massimi [o minimi]relativi della funzione f(*) non vincolati
b)si determina quali dei massimi [o minimi] trovati in a) sono compatibili con i vincoli
c)si sceglie dei punti trovati in a) e b) quello al quale corrisponde il valore massimo [o minimo] di f(*) e lo si chiama [x*,y*]
d)per ognuno dei k vincoli, applicando il metodo dei moltiplicatori di Lagrange, si trova il valore di x e y che massimizza [o minimizza] f(*) con la condizione gi(x,y)=0 per i=1,2,...,k. Se tale punto di massimo [o minimo] esiste ed è compatibile con gli altri vincoli lo si indica con [xk,yk]
e)supposto k>1, per ognuna delle n=k*)k-1)/2 coppie di vincoli si calcolano i punti estremi, definiti come le soluzione delle coppie di eqiazioni gi(x,y)=0,gj(x,y)=o con i<>j e si consoderano solo quelli compatibili con gli altri vincoli. Tra queli punti così trovati si sceglie quello per cui f(*) ha il valore massimo [o minimo] e lo si indica con [xm,ym] per m=1,2,...,n
f)tra i vettori a due dimensioni [x,y] trovati in c),d) ed e) si sceglie quello al quale corrisponde il valore massimo [o minimo] di f(*). Se tale punto esiste, esso sarà la soluzione del problema…
Nel caso illustrato da mica81 [non particolarmente utile come esempio…] si ha…
f(x,y)= x^3+y^2
g1(x,y)=x-1/4
g2(x,y)=y^2-x^2+1 [2]
Il problema consiste nel trovare il valore che rende massima la funxione f(*)=x^3+y^2 nei punti del piano x,y che hanno ascissa…
¼<=x<=sqr (y^2+1) [3]
… e nessun limite per l’ordinata. La ricerca del massimo assoluto di f(*) senza vincoli rivela che essa non ha massimi né minimi in nessun punto del piano x,y. La ricerca eseguita sulla retta x=1/4 [g1(*)=0] rivela un solo punto di minimo [e non di massimo] per y=0 e in essa si ha f(*)=1/64. La ricerca eseguita sulla curva y=sqr(x^2-1) [g2(*)=0] rivela che vi è un punto di minimo [e non di massimo] in [1,0], e lì la fuznione vale 1. In conclusione la fuiznione non presenta massimi e si ha un minimo in [1/4,0] che vale 1/64. In effetti il problema proposto come esempio non è dei più interessanti. Ritengo però si possa certamente fare una scelta migliore…
cordiali saluti
lupo grigio

- lupo grigio
il problema non sarà dei più interessanti...ma chissà come mai era una prova scritta di un esame. guarda qui:
http://www.ing.unipi.it/~d6137/pm/21-6-04.pdf
e poi io penso che ogni esempio non sia banale per imparare a svolgere qualsiasi tipo di problemi.
http://www.ing.unipi.it/~d6137/pm/21-6-04.pdf
e poi io penso che ogni esempio non sia banale per imparare a svolgere qualsiasi tipo di problemi.
- mica81
- Junior Member

- Messaggio: 97 di 135
- Iscritto il: 08/04/2003, 10:34
- Località: Italy
Se ti puo' interessare, guarda qui http://www.llussardi.it/esrcit.MI.pdf
Sono dispense scritte da me per le esercitazioni del Corso di Analisi B che ormai da 3 anni tengo al Politecnico di Milano. Trovi esercizi su massimi e minimi vincolati, ed anche un accenno alla Teoria.
Luca77
http://www.llussardi.it
Sono dispense scritte da me per le esercitazioni del Corso di Analisi B che ormai da 3 anni tengo al Politecnico di Milano. Trovi esercizi su massimi e minimi vincolati, ed anche un accenno alla Teoria.
Luca77
http://www.llussardi.it
- Luca77
Un problemino abbastanza interessante [credo più di quello fornito nell'esempio iniziale...] di massimizzazione può essere il seguente...
<font color="blue">Si deve dimensionare una scatola per spedizioni postali. L’obiettivo è ottenere il massimo di volume compatibilmente con i vincoli imposti dai regolamenti postali. Questi stabiliscono che la somma delle tre quantità 2*w, 2*h ed l non superi i 100 cm [vedi figura]...
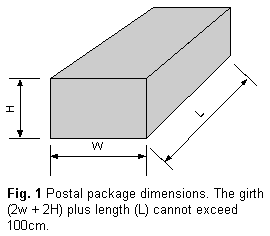
Indicando con x la larghezza, con y l’altezza e con z la lunghezza è possibile porre subito 2*x+2*y+z=100, per cui il problema alla fine si riduce al seguente…
Massimizzare
f(x,y)= 100*x*y–2*x^2*y-2*x*y^2 [1]
con le condizioni…
x>0, y>0, 50-x-y>0 [2]</font id="blue">
Ai volonterosi auguro buon lavoro...
cordiali saluti
lupo grigio

<font color="blue">Si deve dimensionare una scatola per spedizioni postali. L’obiettivo è ottenere il massimo di volume compatibilmente con i vincoli imposti dai regolamenti postali. Questi stabiliscono che la somma delle tre quantità 2*w, 2*h ed l non superi i 100 cm [vedi figura]...

Indicando con x la larghezza, con y l’altezza e con z la lunghezza è possibile porre subito 2*x+2*y+z=100, per cui il problema alla fine si riduce al seguente…
Massimizzare
f(x,y)= 100*x*y–2*x^2*y-2*x*y^2 [1]
con le condizioni…
x>0, y>0, 50-x-y>0 [2]</font id="blue">
Ai volonterosi auguro buon lavoro...
cordiali saluti
lupo grigio

- lupo grigio
Non mi pare che il problema da me proposto abbia suscitato curiosità da parte di qualcuno… pazienza, darò la soluzione e proverò a cercarne un altro più interessante…
Come già illustrato nel procedimento generale si cercano da prima i massimi non vincolati e di essi si sceglie il maggiore compatibile con i vincoli. La funzione da massimizzare è…
f(x,y)= 100*x*y-2*x^2*y-2*x*y^2 [1]
Di essa si calcolano le derivate parziali e si eguagliano a zero…
df/dx= 100*y-4*x*y –2*y^2=0
df/dx= 100*x-4*x*y-2*x^2=0 [2]
Le soluzioni del sistema di due equazioni in due incognite sono x=y=0 e x=y=50/3. Alla prima corrisponde evidentemente un minino, alla seconda un massimo assoluto. Dal momento che il massimo trovato è compatibile con i vincoli la soluzione del problema è x=y=50/3 cm e z=100/3 cm cui corrisponde una scatola di x*y*z=9259.259… centimetri cubici.
cordiali saluti
lupo grigio

Come già illustrato nel procedimento generale si cercano da prima i massimi non vincolati e di essi si sceglie il maggiore compatibile con i vincoli. La funzione da massimizzare è…
f(x,y)= 100*x*y-2*x^2*y-2*x*y^2 [1]
Di essa si calcolano le derivate parziali e si eguagliano a zero…
df/dx= 100*y-4*x*y –2*y^2=0
df/dx= 100*x-4*x*y-2*x^2=0 [2]
Le soluzioni del sistema di due equazioni in due incognite sono x=y=0 e x=y=50/3. Alla prima corrisponde evidentemente un minino, alla seconda un massimo assoluto. Dal momento che il massimo trovato è compatibile con i vincoli la soluzione del problema è x=y=50/3 cm e z=100/3 cm cui corrisponde una scatola di x*y*z=9259.259… centimetri cubici.
cordiali saluti
lupo grigio

- lupo grigio
9 messaggi
• Pagina 1 di 1
Torna a Analisi Numerica e Ricerca Operativa
Chi c’è in linea
Visitano il forum: Yahoo [Bot] e 1 ospite